Arvutamise seadused
Liitmise vahetuvusseadus (kommutatiivsuse seadus)
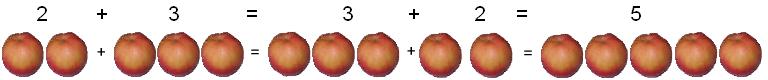
Summa ei muutu, kui muudame liidetavate järjekorda.
2 + 3 = 3 + 2 = 5
a + b = b + a
Sulle võivad huvi pakkuda need õppematerjalid:
Liitmine ja lahutamine 20 piires
II kooliastme matemaatika reeglite kordamine
xy-koordinaatsüsteem
Kirjalik liitmine
Ruumilised kujundid
Ratsionaalavaldised
Ruutjuur, tehted ruutjuurtega
Ruutvõrrandi abil lahenduvad tekstülesanded
Hariliku murru kordamine
Liitmine ja lahutamine 10 piires
Funktsioonide graafikud
Liitmine 20 piires
Ruutvõrrandi mõiste, ruutvõrrandi lahendivalem, ruutvõrrandi liigid
Funktsioonid ja nende graafikud
Kirjalik lahutamine
Funktsioonide graafikute lõikepunktide leidmine
Lahutamine 20 piires
Peastarvutamine eelkoolile
8. klassi matemaatika teooriavideod
Numbrilised seosed
Liitmise ühenduvusseadus (assotsiatiivsuse seadus)
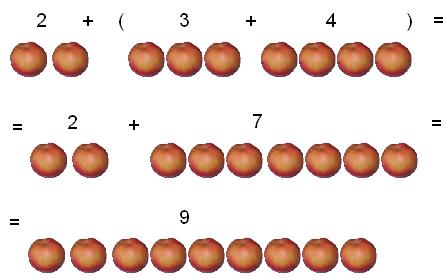
2 + (3 + 4) = 9
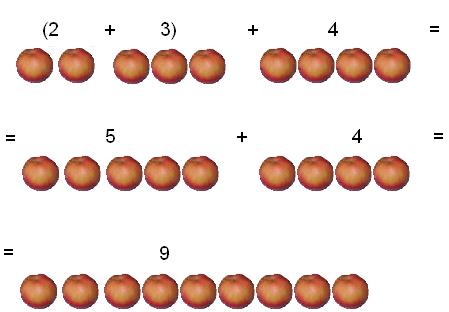
(2 + 3) + 4 = 9
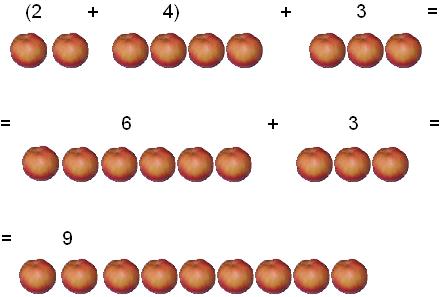
(2 + 4) + 3 = 9
Kahe arvu summa liitmiseks mingi arvuga võib liita selle arvuga enne ühe liidetava ja siis tulemusega teise liidetava.
2 + (3 + 4) = (2 + 3) + 4 = (2 + 4) + 3 = 9
a + (b + c) = (a + b) + c = (a + c) + b
Seda seadust on hea kasutada peastarvutamisel.
17 + (29 + 13) = (17 + 13) + 29 = 30 + 29 = 59
Korrutamise vahetuvusseadus (kommutatiivsuse seadus)
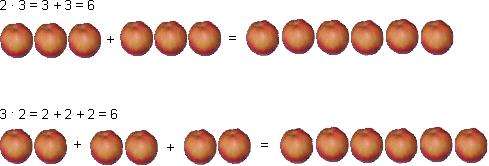
Korrutis ei muutu, kui muudame tegurite järjekorda.
2 · 3 = 3 · 2 = 6
a · b = b · a
Korrutamise ühenduvusseadus (assotsiatiivsuse seadus)
Kahe arvu korrutise korrutamisel mingi arvuga võib selle arvuga korrutada esmalt ühe teguri ja tulemusega teise teguri.
 Mitu sellist kuupi vajatakse järgmiste risttahukate ladumiseks?
Mitu sellist kuupi vajatakse järgmiste risttahukate ladumiseks?
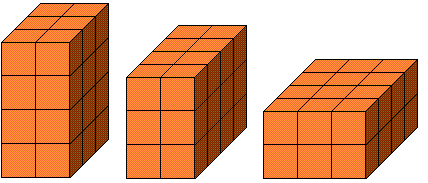
Kõik need risttahukad koosnevad 2 · 3 · 4 kuupidest.
Risttahukatel on erinevad põhja pindalad: 2 · 3, 2 · 4 ja 3 · 4.
Samuti on neil erinevad kõrgused: 4, 3 ja 2.
V = SP · H
(2 · 3) · 4 = (2 · 4) · 3 = 2 · (3 · 4) = 24
a · (b · c) = (a · b) · c = (a · c) · b
Korrutamise jaotuvusseadus (distributiivsuse seadus)
Summa korrutamiseks mingi arvuga võib korrutada selle arvuga iga liidetava ja tulemused liita.

Ühes reas on 3 + 5 ringi, kahes reas on 2 · (3 + 5) = 2 · 3 + 2 · 5 = 16 ringi.
Punaseid ringe on 2 · 3, valgeid ringe on 2 · 5. Kokku on 2 · 3 + 2 · 5 = 16 ringi.
a · (b + c) = a · b + a · c
Seadust on hea kasutada peastarvutamisel.
7 · (10 + 8) = 7 · 10 + 7 · 8 = 70 + 56 = 126
18 · 11 = 18 · (10 + 1) = 18 · 10 + 18 · 1 = 180 + 18 = 198