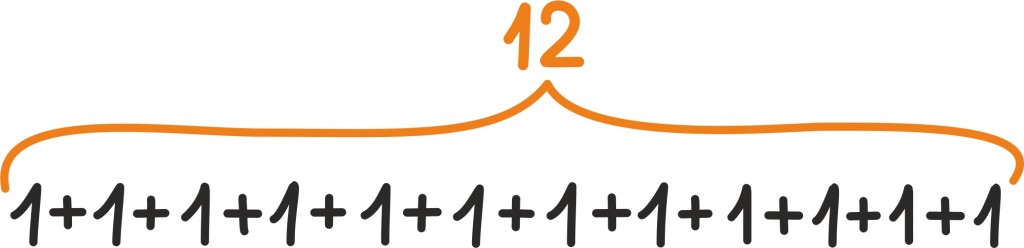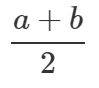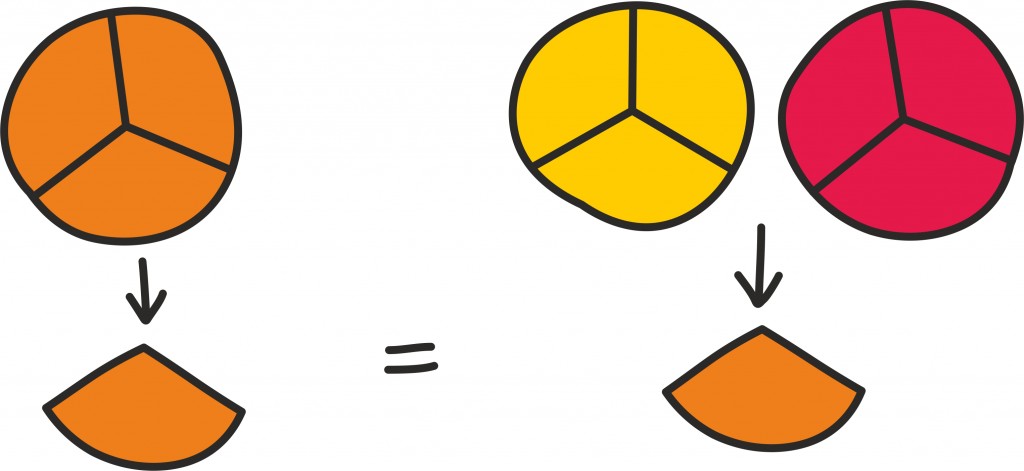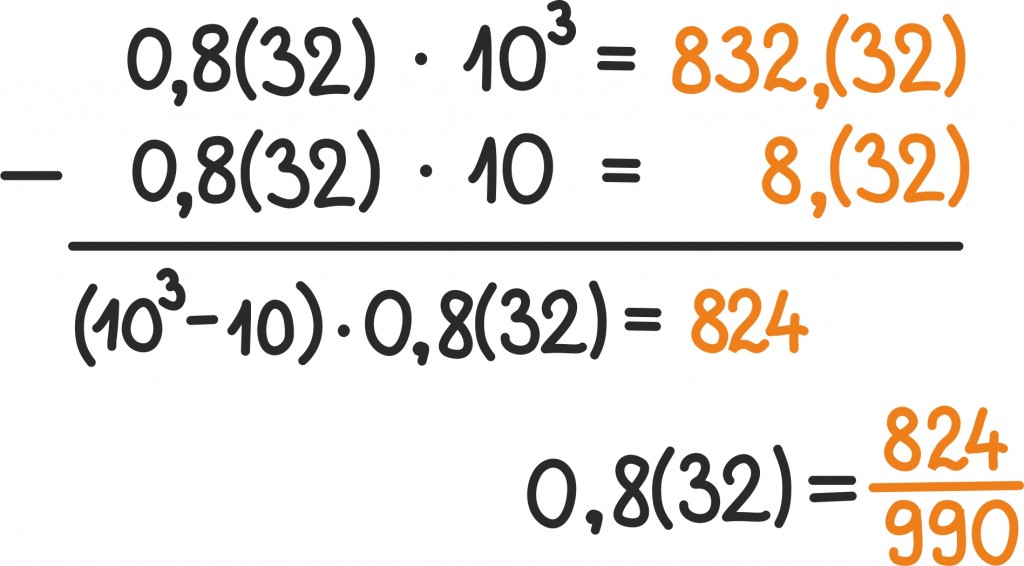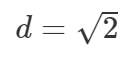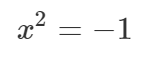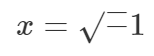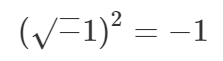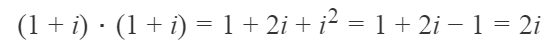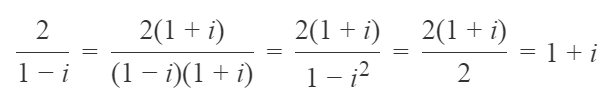Arvhulgad
Naturaalarvud
Naturaalarvud on arvud, millega loendame õhtul lambaid: 1, 2, 3, 4, 5, 6, … Neid kõiki korraga ehk nende hulka tähistatakse N-iga.
Naturaalarvud on ilmselt kõige loomulikumad matemaatilised objektid, lihtsad, aga tähtsad. Kuna nad tulevad esile kohe, kui loendama hakkame, ei saa nendest maailma kirjeldamisel üle ega ümber.
Oma loomulikkuse tõttu on nad ka matemaatikas üheks keskseks objektiks ja nende uurimine pole veel sugugi päris lõppenud!
Naturaalarvude matemaatiline kirjeldamine
Naturaalarvud võib üles ehitada ühe arvu – arvu 1 – ning ühe tehte – arvu 1 liitmise baasil. Iga naturaalarvu võime leida, kui ühte piisava arvu kordi iseendaga kokku liidame. Arvu 10 saamiseks peame näiteks arvule 1 veel 9 arvu 1 juurde liitma.
Nii leidub igast naturaalarvust veel ühe võrra suurem naturaalarv. Näiteks isegi kui meil on juba 1000 sõpra, võiksime leida veel ühe sõbraliku selli Tiibeti mägedest ning meil olekski juba 1001 sõpra – ka teda peame oskama arvestada!
Seega kõige suuremat naturaalarvu ei leidugi. See arusaam võib alguses tunduda natuke üllatav, aga teiselt poolt: kas on mingi põhjus, miks peaks leiduma kõige suurem arv? Nii kohtame ka esimest korda lõpmatust – naturaalarve peab kokku olema lõpmatult palju.
Naturaalarve võib kirjeldada ja defineerida ka mitmel muul moel. Näiteks võite hulkade peatükist lugeda, kuidas naturaalarve kirjeldada ainuüksi hulkade abil [lk 61].
Tasub ilmselt veel ära märkida, et mõnikord loetakse ka 0 naturaalarvude hulka, tähistamaks olukorda, kus veel midagi loendatud pole. See on aga rohkem maitse küsimus, nii et lugeja võib täiesti vabalt ise otsustada, kas 0 on naturaalarv või pole. Meie positsioon on aga selge: alustasime ju raamatus esinevate osade loendamist just nullist.
Naturaalarvude tähistamine
Naturaalarvud on väga loomulikud, nad on erinevates kultuuriruumides sõltumatult kasutusele võetud ja välja on arenenud erinevad tähistused. Järgnevalt tutvustame nendest ka mõnda levinumat.
Kümnendsüsteem
Meile on kombeks naturaalarve tähistada kümne numbri abil 0, 1, 2, 3, 4, 5, 6, 7, 8 ja 9.
Kuna kasutame täpselt kümmet erinevat sümbolit, siis sellist tähistust nimetataksegi kümnendsüsteemiks. Kümnendsüsteemis ehitame kõik arvud üles ühelistest, kümnelistest, sajalistest (kümme korda kümme), tuhandelistest (kümme korda kümme korda kümme) ja nii edasi – kümnete meri.
Näiteks arv 128 tähendab lahtikirjutatult 1 · 10 · 10 + 2 · 10 + 8
ning arv 9301 tähendab 9 · 10 · 10 · 10 + 3 · 10 · 10 + 0 · 10 + 1.
Arvu astme peatükis [lk 110] näeme, et võime ühelised, kümnelised, sajalised ja nii edasi kõik kirjutada arvu kümme astmete abil – lisame 10 ülemisse paremasse nurka tema astendaja, mis ütleb, mitu korda arvu 10 kokku korrutame:
Nii võime arvu 9301 kirjutada veelgi kompaktsemalt:
Kahendsüsteem
Arvutitekogus toimub arvutamine aga kahendsüsteemis – kõik arvud kirjutatakse kahe numbri 0 ja 1 abil ja arve loendatakse mitte kümneliste, vaid kaheliste kaupa. Näiteks arvu 3 kuju kahendsüsteemis on 11, kuna 3 = 1 · 2 + 1, arv 5 on kujus 101 kuna 5 = 1 · 2 · 2 + 0 · 2 + 1 ning arv 8 on kujus 1000, kuna 8 = 1 · 2 · 2 · 2. Sarnaselt kümnendsüsteemiga võime seega iga naturaalarvu kirjutada üldkujus arvu 2 astmete abil.
Enne juba käsitletud arvu 9301 võime seega kahendsüsteemis kirja panna pisut pikemalt:
Teisisõnu on kahendsüsteemis arvu 9301 kujuks 10010001010101.
Kindlasti tuleks küsida: miks ikkagi arvutites kõik kahendsüsteemis toimub? Põhjus on väga proosaline – kahendsüsteemis on meil vähim erinevaid sümboleid, mida kuidagi masinavärgis tähistama peaks. Kõige lihtsam ongi arvutit üles ehitada „lülititest”, millel on täpselt kaks olekut – kas sees või väljas. Need vastavad siis väärtustele 1 ja 0. Nii on kahendsüsteemis lihtsam arve salvestada ja lihtsam ka tehteid teha. Mõelge ise, on ju endalgi kahte ühte ja nulli omavahel lihtsam kokku liita kui näiteks seitset ja viit.
Ainus raskus võrreldes kümnendsüsteemiga on arvude lugemine – arvud lähevad kiiresti maru pikaks. Meil igapäevaelus oleks see probleem, aga arvuti võib ju ekraanile meie jaoks midagi mugavamat kuvada.
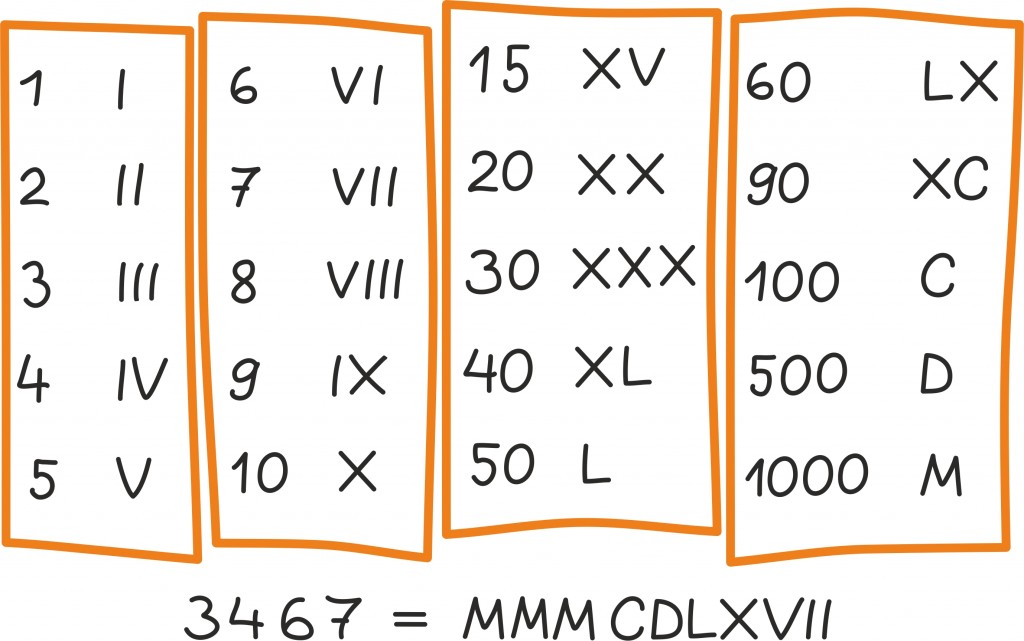
Rooma numbrid
Roomlased vedasid aga naturaalarvude tähistamiseks hoopis kummalisi kriipse: näiteks meie ühte tähistati kriipsuga I, meie 12 kriipsudega XII ja meie 49 kriipsudega IL.
Proovige leida reegleid Rooma numbrite liitmiseks või veel hullem, korrutamiseks. Näiteks liidaksid roomlased arve 69 ja 145 kokku järgnevalt.
LXIX + CXLV
1. Tuleb asendada kõik „lahutavad liikmed”:
LXVIIII + CXXXXV
2. Kokku panna:
LXVIIIICXXXXV
3. Sorteerida:
CLXXXXXVVIIII
4. Kombineerida gruppidesse:
CCXIIII
5. Asendada lahutavad liikmed tagasi:
CCXIV
Veendute ilmselt üsna kiiresti, et sellise arvusüsteemiga on peaaegu võimatu aritmeetikat teha. Ning tõepoolest, roomlased oma matemaatilistelt teadmistelt või tegudelt ajaloos just silma ei paista.
Teisendamine
Oletame, et teie mitte eriti hea sõber on otsustanud põikpäiselt kasutada kahendsüsteemi ja väidab teile, et olete talle võlgu täpselt 101010 eurot. Loetuna kümnendsüsteemis oleks see päris märkimisväärne summa, nii et ilmselt tasub üritada arv kahendsüsteemist kümnendsüsteemi üle viia. Kuidas seda teha?
Kõik on tegelikult juba eelnevalt välja toodud. Kirjutame kõigepealt välja, mida 101010 kahendsüsteemis tähendab: 101010 = 25 + 23 + 2. Edasi kirjutame lihtsalt kõik toodud kahe astmed kümnendesitluses: 25 = 32, 23 = 8, 2 = 2. Lõpetuseks peame saadud arvud (nüüd kümnendesitluses) oma tavaliste liitmisnippidega kokku liitma: saame vastuseks 42.
Sulle võivad huvi pakkuda need õppematerjalid:
Ruutvõrrand
Numbrilised seosed
Funktsioonide graafikute lõikepunktide leidmine
Üksliikmed, hulkliikmed ja tehted nendega
Ruutjuur, tehted ruutjuurtega
Lahutamine 20 piires
Kirjalik liitmine
Algebralised murrud
Funktsioonide graafikud
Ruumilised kujundid
8. klassi matemaatika teooriavideod
Peastarvutamine I kooliastmele
II kooliastme matemaatika reeglite kordamine
Liitmine 10 piires
Kell ja kellaaeg
Peastarvutamine eelkoolile
xy-koordinaatsüsteem
Harjutusülesandeid matemaatika riigieksamiks
Liitmine ja lahutamine 20 piires
Funktsioonid ja nende graafikud
Täisarvud
Naturaalarvud on juba väga toredad, aga nendega tuleb esile ka mõningaid probleeme.
Naturaalarve saame omavahel liita ja summaks on alati naturaalarv: näiteks 3 + 4 = 7 või 2 + 10 = 12. Liitmisest võib siin väga vabalt mõelda lihtsalt loendamise raames: keegi annab teie kolmele õunale neli lisaks või näiteks lisaks teile ja kassapidajale siseneb äkiliselt poodi veel 10 tantsulist.
Tore oleks, kui saaksime ka kuidagi kirjeldada olukorda, kus neli õuna jälle tagasi küsitakse või kus 10 tantsulist jälle poest välja kepslevad. Ütlete kohe, et selleks on muidugi lahutamine: 7 – 4 = 3 või 12 – 10 = 2.
Tekib aga probleem: kui mul on ainult 3 õuna, ei saa mult nelja õuna ära võtta ja kui poes on ainult 2 inimest, ei saa sealt 10 ära minna. Seega osasid arve justkui ei saakski omavahel lahutada.
Veider! Mis on need arvud, mis võiksid tähistada midagi, mis on vähem kui mitte midagi?
Ja kuigi pakuti juba varakult välja, et tegelikult võiksid eksisteerida ka arvud 3 – 4 ning 2 – 10, ei tahetud nendega pikka aega leppida. Neid peeti ebaloomulikeks. Mida peaks tähendama see –1, mida mõni pakkus 3 – 4 vastuseks, või –8, mida pakuti 2 – 10 vastuseks? Kui miski eksisteerib, on teda ju vähemalt üks? Kuidas saab olemas olla mitte millestki veel väiksem kogus?
Tänapäeval kahjuks teab mõni seda liigagi hästi, mida negatiivsed arvud tähistada võivad – näiteks võlga! Katsetage internetis oma pangakontoga, ta võib kergesti sattuda ka miinusesse, kui raha liiga agarasti kulutada. Arvust –1 võibki näiteks mõelda kui õunavõlast vanemale vennale…
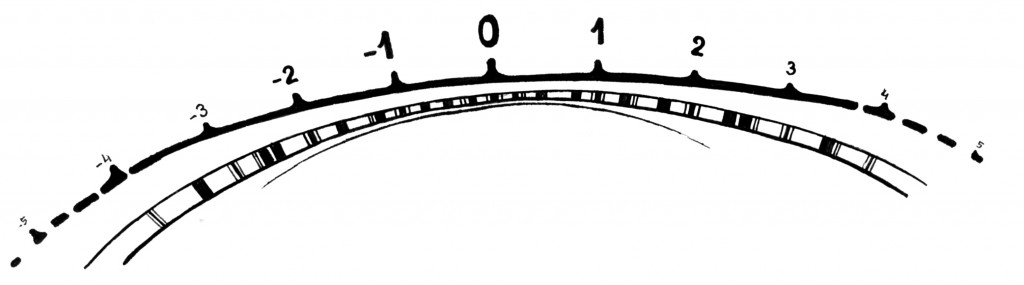
Sellega, et negatiivsed arvud on täiesti mõistlikud ja isegi loomulikud, lepiti aga alles 19. sajandil. Enne seda kutsuti neid küll absurdseteks, küll räpasteks ja tihti keelduti nendega igasugusest läbikäimisest. Tegelikult on ju negatiivsete arvudega siiski toredam ja ilusamgi – nende abil ei jää arvsirge poolikuks, vaid on kenasti alguse ja lõputa.
Arvude liitmisest ja lahutamisest võimegi mõelda kui arvsirgel paremale või vasemale poole liikumisest – liites neli, liigume neli sammu paremale; lahutades seitse, seitse sammu vasemale. Kõiki täisarve võime omavahel liita ja lahutada ning alati jälle vastuseks täisarvu saada.
Täisarvude hulka tähistatakse Z-iga.
Ratsionaalarvud
Ometigi ei paku ka täisarvud veel täit rahulolu! Tõepoolest, lihtne on võrdselt jagada kuus õuna kolme sõbra vahel – annad kõigile kaks. Ent kuidas võrdselt jagada üht suurt arbuusi kolme sõbra vahel?
Meil on muidugi vastus olemas, igale sõbrale tuleb anda kolmandik arbuusist. Probleem on aga, et kolmandik ei ole täisarv – peame jagamise jaoks arve veel mängu juurde tooma. Piisab sellest, kui võtame appi kõik arvud, mis saame täisarvude jagamisel nullist erinevate täisarvudega.
Selliseid arve nimetatakse ratsionaalarvudeks – nad on kujus p⁄q, kus p ja q on täisarvud. Ratsionaalarvud on näiteks 2⁄3, -1⁄2, 231⁄100, aga ka kõik täisarvud, sest näiteks 2 = 2⁄1.
Murrujoone peal olevat arvu nimetatakse murru lugejaks ja murrujoone all asuvat arvu murru nimetajaks. Ratsionaalarvude hulka tähistatakse tähega Q.
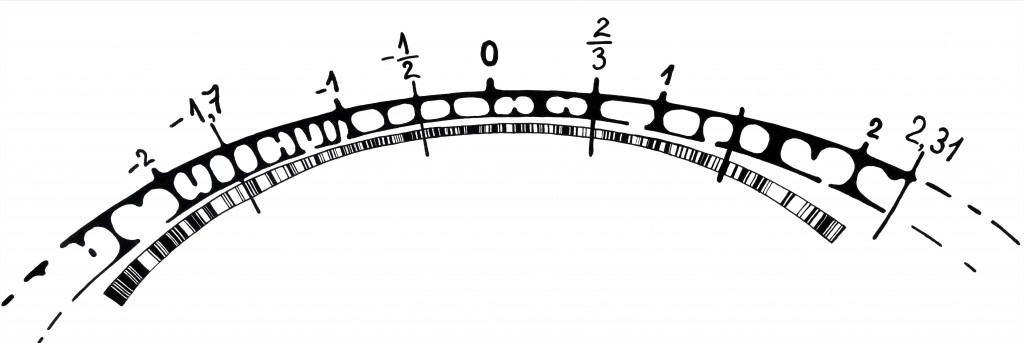
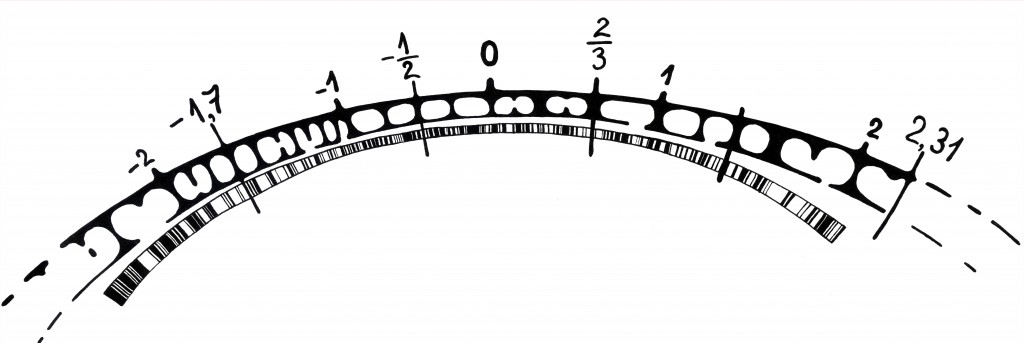
Hakates arvjoonele usinalt ratsionaalarve kirja panema, märkame, et neid on väga palju ja nad asuvad arvteljel ütlemata tihedalt. Tegelikult asub iga kahe ratsionaalarvu vahel alati veel üks ratsionaalarv: näiteks arvude –2 ja –1 vahel asub arv –1,7, arvude 2 ja 2,4 vahel 2,31. Üldisemalt, iga kahe suvalise ratsionaalarvu a ja b vahel asub ju nende aritmeetiline keskmine
Taandatud murrud ja tehted
Ütlesime, et kõik ratsionaalarvud saame, kui jagame täisarve nullist erinevate täisarvudega. Nii saame tegelikult liiga palju arve – paljud neist on omavahel võrdsed. See on küll väga lihtne, aga oluline tähelepanek.
Tõepoolest, kuna kahe arbuusi jagamisel kuueks võrdseks tükiks on tükid sama suured kui ühe arbuusi jagamisel kolmeks võrdseks osaks, ei ole mitte kõik täisarvude omavahelisel jagamisel saadud arvud erinevad, näiteks 2⁄6 = 1⁄3.
Kuna mitmed murrud on omavahel võrdsed, oleks tore leida neile kõigile üks parim esindaja. Selleks on murru taandatud esitus. Murru taandatud esituse saamiseks jagame murru nimetaja ja lugeja kõikide nende ühiste teguritega läbi: nii ongi näiteks ratsionaalarvude 1⁄3 , 2⁄6 ja 4⁄12 kõikide ühiseks taandatud kujuks 1⁄3 .
Ratsionaalarvudega on veelgi ohutum ja sujuvam ringi käia kui täisarvudega. Nimelt võime kõiki ratsionaalarve omavahel lisaks liitmisele-lahutamisele ka korrutada ja jagada (siiski mitte nulliga!) ning saame alati jällegi tulemuseks ratsionaalarvu.
Kümnendesitus
Ratsionaalarvudel leidub ka esitus kümnendsüsteemis, kasutusele tuleb lihtsalt võtta komakohad.
Näiteks ½ = 0,5, 13⁄8 = 1,625 ning 1⁄3 = 0,(3), kus sulgudes olev kolm tähistab, et number 3 jääb lõpmatult korduma.
Selgub, et iga ratsionaalarvu saabki esitada kümnendsüsteemis kas lõpliku arvu komakohtadega nagu 1⁄8 = 0,125 või lõpmatult korduma jäävate komakohtadega: näiteks 1⁄7 = 0,(142857) ja 1⁄12 = 0,08(3). Teisel juhul esile tulevaid kümnendesitusi nimetatakse perioodilisteks.
Järgnevalt selgitame natuke lähemalt, miks ratsionaalarvud on just nimelt kas lõpliku või perioodilise kümnendesitusega. Näitame esmalt, et iga lõpliku või perioodilise kümnendesitusega arv on ratsionaalarv:
Oletame, et meil on lõpliku kümnendesitusega arv.
Sel juhul võime arvu korduvalt 10-ga korrutades komakohtadest lahti saada. Näiteks kui arvul on kaks komakohta nagu arvul 0,25, peame seda täisarvu saamiseks korrutama 10-ga täpselt kaks korda – konkreetsel juhul on saadavaks täisarvuks 25. Ja edasi võime juba lihtsalt avaldada arvu 0,25 kahe täisarvu jagatisena, kui jagame võrrandi mõlemad pooled 100-ga läbi.
Oletame, et meie arv on perioodiline kümnendesitus.
Nüüd võime korduvalt kümnega korrutades komakohta liigutada nii palju, et pärast koma jääks alles ainult perioodiline osa. Kui näiteks periood algab üks koht pärast koma, peame korrutama kümnega. Näiteks arvu 0,8(32) korral saame arvu 8,(32).
Edasi võime aga jätkata kümnega korrutamist nii kaua, kuni algab perioodilise osa teine tsükkel. Kui perioodi pikkus on kaks, peame juba saadud arvu veel 100-ga korrutama. Konkreetsel juhul saaksime siis arvu 832,(32).
Lahutades nüüd teisest arvust esimese, jääb alles täisarv – perioodiline osa pärast komakohta taandub ju täpselt välja. Edasi saame juba lihtsalt avaldada arvu 0,8(32) ratsionaalarvuna.
Miks vastupidi igal ratsionaalarvul peaks just kirjeldatud kümnendesitus leiduma, on juba pisut kavalam ja jääb siinkohal tõestamata.
Oluline on ka ära märkida, et kümnendesitus ei ole alati ühene. Näiteks matemaatilise võrduse peatükis [lk 52] näitame, et 1 = 0,(9).
Irratsionaalarvud ja reaalarvud
Ratsionaalarvudega saame loendada, liita ja lahutada, korrutada ning jagada. Tundub, et seda on juba päris palju. Üllatuslikult võime aga endiselt välja tulla geomeetrilise konstruktsiooniga, mille kirjeldamiseks ratsionaalarvudest ei piisa.
Ühikruudu diagonaali pikkus ei ole ratsionaalarv!
Joonistame ilusa ühikruudu ja leiame selle ühikruudu diagonaali pikkuse.
Tähistades seda diagonaali d-ga, teame näiteks Pythagorase teoreemist, et d2 = 2. Loomulik küsimus on: kas d on ikka ratsionaalarv?
Oletame, et d on tõesti ratsionaalarv: sel juhul võime dkirjutada taandatud kujus p⁄q , kus p ja q on täisarvud ning neil ei ole ühiseid tegureid. Saame, et p2 = 2q2.
Aga nüüd on ju võrdusmärgist paremal pool paarisarv, seega peab ka vasemal olema paarisarv. Kui p2 on paarisarv, siis ei saa p paaritu olla, sest paaritu arv ruudus annab paaritu arvu. Järelikult ka p on paarisarv ja võime p kirjutada kujul p = 2a.
Seega võime p2 kirjutada kui (2a)2 = 4a2. Asendades selle esialgsesse valemisse saame 4a2 = 2q2. Jagades kahega läbi, jääb alles 2a2 = q2.
Nüüd on aga vasem pool paaris ning seega peab ka qjaguma kahega. See on aga vastuolus meie eeldusega, et p⁄q oli taandatud murd. Seega ei saa d kuidagi olla ratsionaalarv, sest muidu jõuame loogilise vastuoluni.
Seega on ta hoopis niinimetatud irratsionaalarv!
Irratsionaalarvud
Oh seda häda, kui Antiik-Kreekas sellele riukale jälile saadi. Nende jaoks olid proportsioonid ehk täisarvude suhted looduse üheks aluseks ning nii ei tahtnud nad sugugi leppida sellega, et leidub geomeetrilisi objekte, mille pikkust ei õnnestugi proportsioonide ehk täisarvude suhete abil kirjeldada. Räägitakse, et mõni matemaatik pidi selle avastuse tõttu lausa elust ilma jääma. Siiski jäädi matemaatikale truuks ja tänaseks ei nähta sellistes irratsionaalarvudes enam suurt ohtu ei tervisele ega ühiskonnale. Tegelikult lepiti nendega hoopis enne kui negatiivsete arvudega – nad tundusid küll kummalised, aga neile oli ometi võimalik looduses ja geomeetrilises ettekujutuses vastet leida.
Irratsionaalarvudeks nimetataksegi kõiki arve arvteljel, millel ei ole esitust kujus p⁄q. Paljud neist on esitatavad täis- või ratsionaalarvude juurtena [lk 111], näiteks
ja ka
on irratsionaalarvud. Irratsionaalarvudeks on aga veel näiteks π ja e. Nende faktide tõestamine on aga päris keeruline ja senini on näiteks teadmata, kas πe on ratsionaalarv või irratsionaalarv.
Ka irratsionaalarvudel leidub kümnendsüsteemis esitus. Ainus mure on, et neid ei saa selles kujus kunagi täpselt esitada – irratsionaalarvude kümnendesitus on lõpmatult pikk. Näiteks arvu π esimesed 20 kohta on 3,14159265358979323846…, aga edasi tulevad jälle täiesti ennustamatud numbrid ning veelgi hullem – neid tuleb lõpmatult palju.
Pannes arvteljele kirja kõik ratsionaalarvud ja irratsionaalarvud, saame lõpuks kokku terve arvtelje – ükski punkt ei jää puudu ega vahele. Kõik arvtelje arvud kokku moodustavad reaalarvude hulga, mida tähistatakse arvuga R.
Kui ratsionaalarvud saime üles ehitada täisarvudest, siis kõikide irratsionaalarvude täpne matemaatiline konstrueerimine on juba veidi keerulisem. Võime küll irratsionaalarvudest mõelda kui arvudest, mida saame kirjutada lõpmatu ja mitteperioodilise kümnendesituse abil, aga kuidas neid liita või korrutada? Õigupoolest jõudsid matemaatikuid rahuldava range kirjelduseni alles 19. sajandil ning selle jaoks võib kasutada piirväärtuseid [lk 319].
Praeguseks on aga tore irratsionaalarvude sissetoomisest mõeldagi geomeetriliselt: irratsionaalarvud täidavad ratsionaalarvudest arvteljele jäänud auke, nende liitmine tähendab – nagu ratsionaalarvude liitminegi – lihtsalt arvtelje nihutamist.
Kompleksarvud*
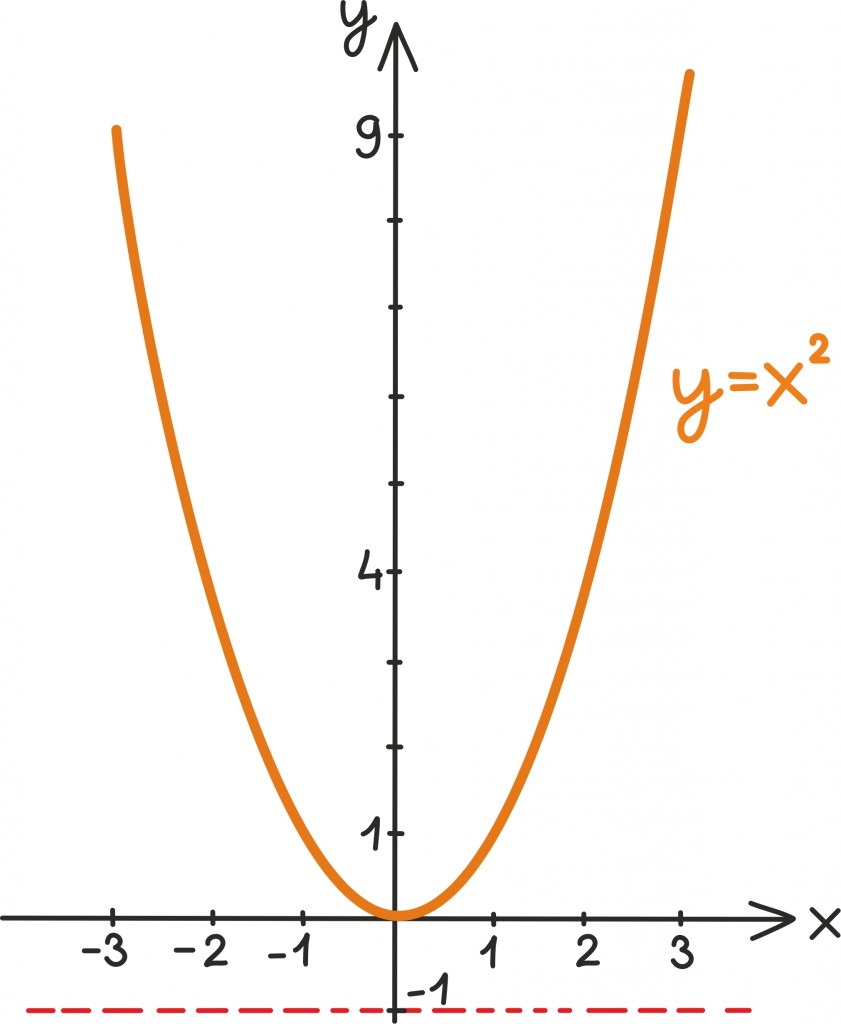
Reaalarvudega saab kõik igapäevatoimetused korda aetud… kui just ei taha igal õhtul leida ruutvõrrandile x2 = –1 lahendit.
Tõepoolest, ükski reaalarvu ruut ei ole ju negatiivne. Näiteks 1 · 1 = 1 ning ka (–1) · (–1) = 1 ehk meie ruutvõrrandi lahendiks ei kõlba 1 ega ka –1. Lihtsam on seda vahest näha isegi ruutfunktsiooni graafikult:
Seega, kui tahame tõesti, et saaksime välja kirjutada lahendit ka ruutvõrrandile x2 = –1 või ruutvõrrandile x2+ x + 1 = 0 või näiteks ka neljanda astme võrrandile x4 + x2 = –3, peame tingimata oma arvusüsteemi veel kord laiendama ja veel rohkem arve kasutusele võtma.
Eelnevat võib ümber sõnastada ka järgmiselt: nägime, et reaalarvude abil saame leida kõik arvud x nii, et x2= a iga mittenegatiivse a jaoks. Kui nüüd tahame aga lahti saada tingimusest „mittenegatiivne“, siis peamegi sisse tooma kompleksarvud.
Kui lubada natukene mõttel lennata, siis võiksime õigustatult võrrandi
lahendiks pakkuda
Tõepoolest, kuna ruutjuure võtmine ning ruutu võtmine taandavad teineteise välja, võime kirjutada
Seega, lubades ruutvõrrandi lahendiks ka uut leiutist √–1, oleme laiendanud arvusüsteemi. Üllataval kombel piisab sellest laiendusest mitte ainult peatüki alguses toodud võrranditele, vaid tegelikult absoluutselt kõikidele polünoomvõrranditele [lk 266] lahendite leidmiseks!
Imaginaararv i ja komplekstasand
Irratsionaalarvude lisamisel toppisime reaaltelje kõik augud täis. Kuhu need kompleksarvud siis mahtuda võiksid?
Märkame, et isegi kui tõmbame paberile ühe aukudeta sirge, jääb paberile veel ruumi kui palju – sirgest üles ja alla jääb mõlemale poole tühjus. Kompleksarvud täidavad kogu selle tühjuse, nad täidavad arvudega terve paberilehe.
Nii on kompleksarvud mingis mõttes kahemõõtmelised arvud: võib öelda, et neil on reaalmõõde ja imaginaar- ehk kompleksmõõde, mille toob kaasa uus sissetoodud arv √–1. Kohe selgitame!
Seda arvu nimetataksegi imaginaararvuks ja kuna teda on tüütu kogu aeg välja kirjutada, anname talle tähiseks i. Nimi imaginaararv tuleneb just sellest, et itundus vähemalt esialgu eksisteerivat ainult matemaatikute endi ettekujutuses ja mitte välises maailmas.
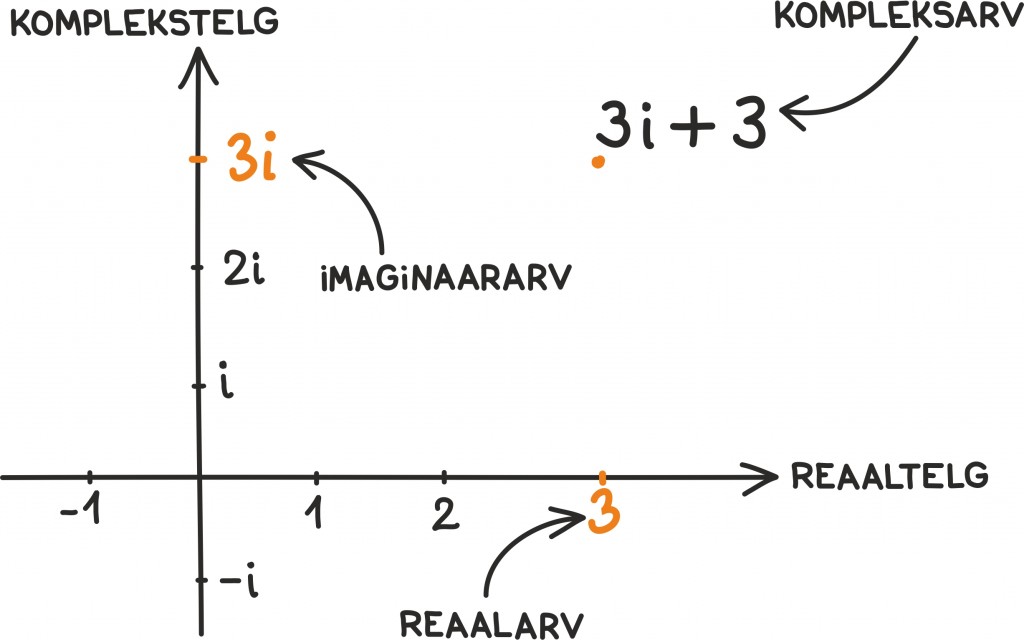
Meenutame, et arvu 1 võib pidada reaalmõõtme ühikuks – seda kokku liites või suurendades-vähendades liigume mööda horisontaaltelge. Sarnaselt on i kompleksmõõtme ühikuks, teda liites või suurendades liigume mööda vertikaaltelge. Ta asub nullpunktist sama kaugel kui reaaltelje ühik.
Nii on teised komplekstelje punktid antavad kujus 2i; 0,3i; 14i ja nii edasi.
Kõikvõimalikud kompleksarvud saame, kui vaatame arve kujus c = a + bi, kus a ja b on reaalarvud. Reaalarvu a kutsutakse kompleksarvu c reaalosaks ja b-d tema imaginaarosaks.
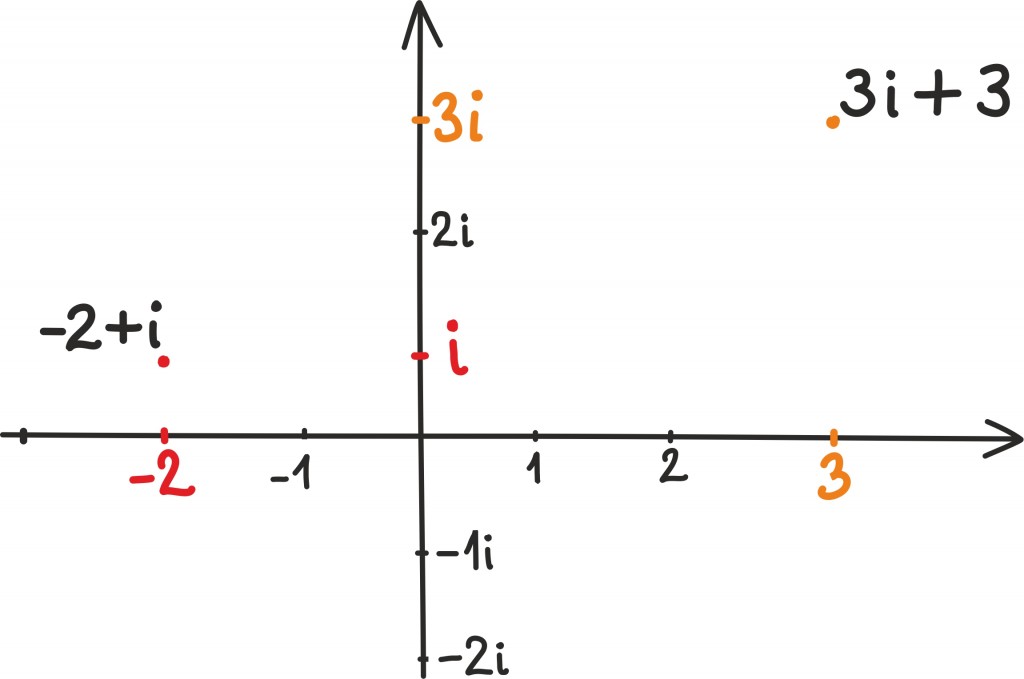
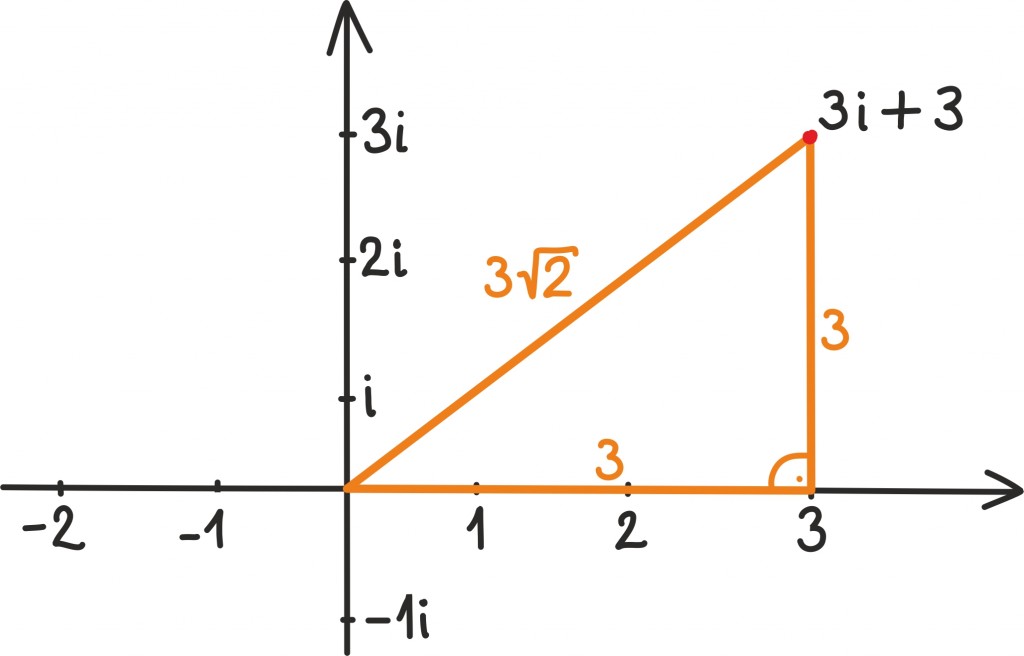
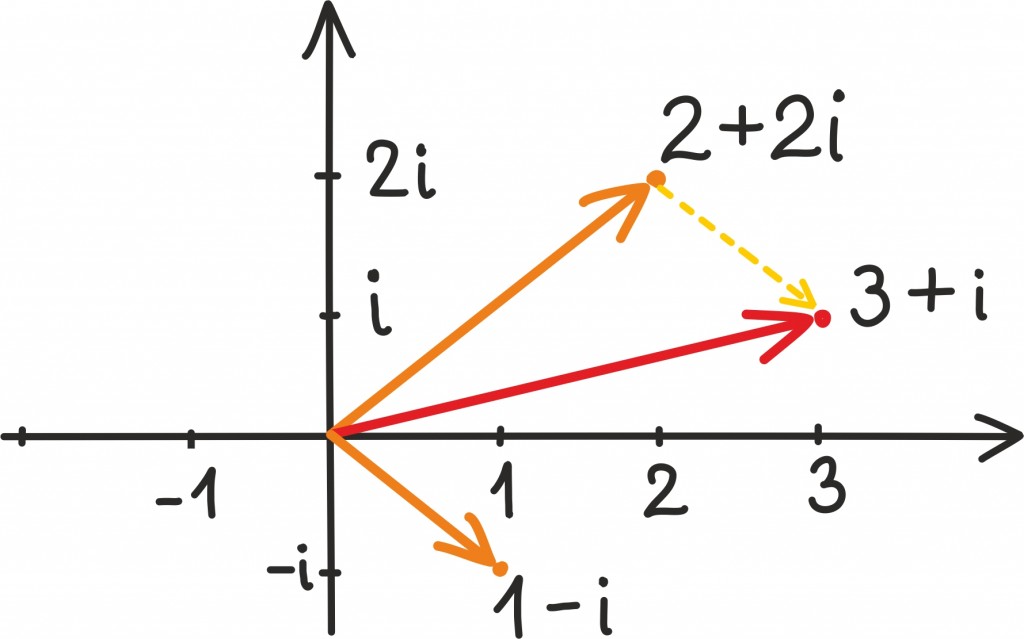
Joonistame komplekstasandile näiteks punktid 3, 3i, 3 + 3i, –2 + i.
Iga reaalarvu korral võime rääkida tema suurusest ehk absoluutväärtusest – peame silmas talle vastava punkti kaugust arvtelje nullpunktist [lk 120]. Samamoodi võime ka iga kompleksarvu korral rääkida tema suurusest – talle komplekstasandil vastava punkti kaugusest nullpunktist. Seda kaugust võib muidugi leida Pythagorase teoreemi abil.
Aga kompleksarve pole ju olemas!
Nagu ennist rääkisime, oli matemaatikutel ja kogu inimkonnal suuri raskusi negatiivsete arvudega – alles paarsada aastat tagasi lepiti, et tegemist on ikkagi täiesti mõistlike ja loomulike arvudega, millega tegelemine ei ole sugugi jumalateotus.
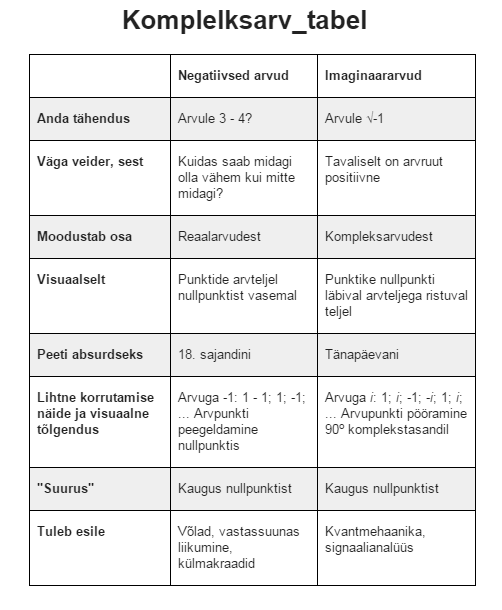
Selles valguses on kompleksarvude mõistlikkuse ja loomupärasuse kahtlustamine igati mõistetav. Järgnev tabel, kus võrdleme negatiivseid arve ja imaginaararve, võiks siiski veenda, et ka kompleksarve pole mõtet karta.
Küsimusele, kas arv 4 + 5i eksisteerib, on muidugi raske vastata, kuid sama raske on öelda, kas arv 4 või 5 eksisteerib. Siiski on kompleksarvud leidnud reaalarvude kõrval tänapäevases maailma ja looduse kirjelduses oma kindla koha.
Tehted kompleksarvudega
Selgub, et kompleksarvud on väga toredad ja nendega saab teha kõike, mida reaalarvudega, ja veel rohkematki.
Liitmine ja lahutamine
Kompleksarve saab liita ja lahutada, tuleb lihtsalt liita ja lahutada eraldi reaal- ja imaginaarosa: näiteks (1 –i) + (2 + 2i) = 3 + i. Nagu reaalarvude liitmisest võib mõelda kui liikumisest ühes või teises suunas reaalteljel, võib ka kompleksarvude liitmisest mõelda geomeetriliselt. Seekord liigume lihtsalt komplekstasandil, vastava arvu samme reaaltelge mööda, vastava arvu imaginaartelge mööda.
Korrutamine ja jagamine
Kompleksarve saab edukalt ka korrutada ja isegi jagada. Tulemuseks on endiselt alati kompleksarv. Näiteks
ning
Kompleksarvudega korrutamisel on ka ilus geomeetriline tõlgendus – tasandil pööramine.
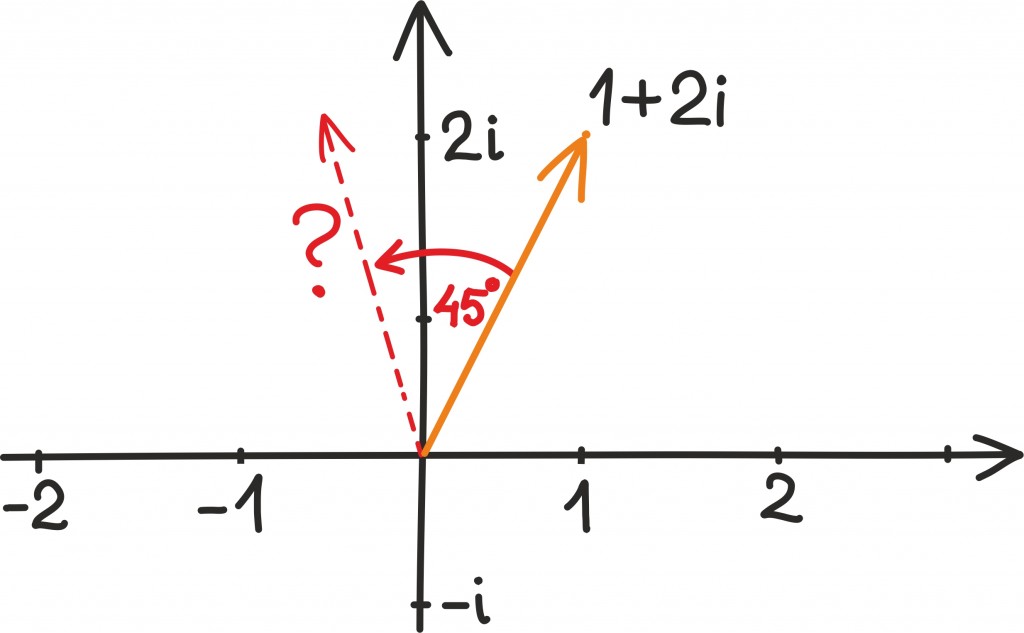
Näiteks oletame, et meile on antud kompleksarv 1 + 2i ning tahame leida uut kompleksarvu, mis on selle arvu suhtes 45-kraadise nurga all vastupäeva.
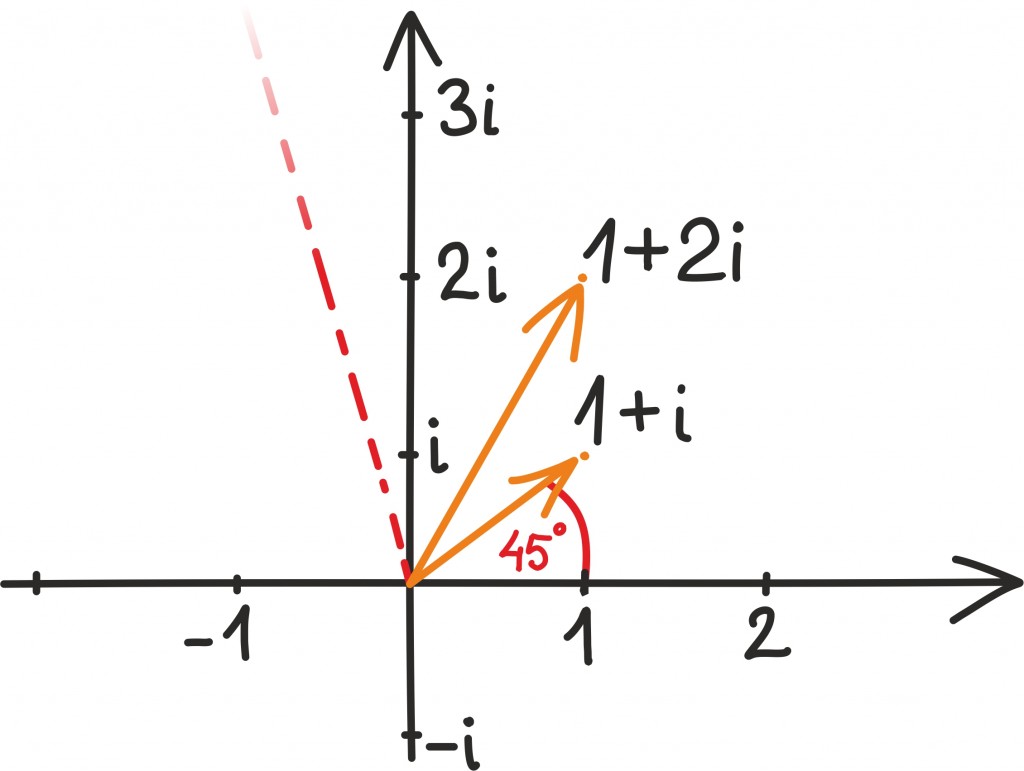
Tuleb välja, et sellise kompleksarvu leidmiseks võime lihtsalt algset arvu korrutada mistahes kompleksarvuga, mis on 45-kraadise nurga all reaaltelje suhtes: näiteks arvuga 1 + i.
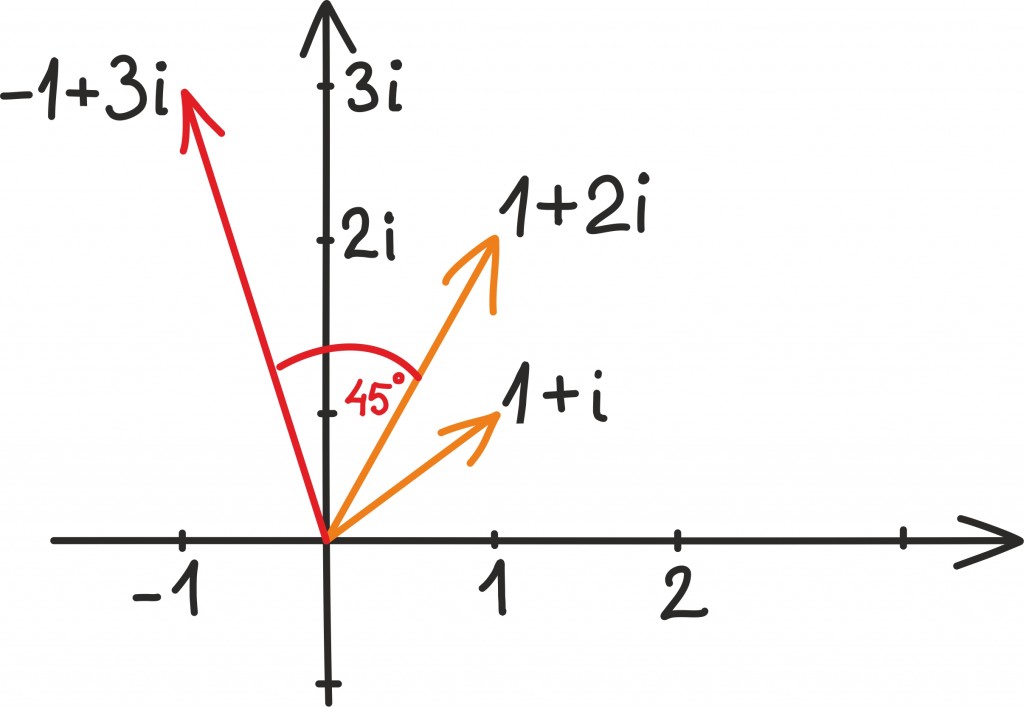
Seda kõike ei pea muidugi joonise põhjal uskuma. (Ei tohigi uskuda!) Õnneks kinnitab aga algebra kenasti meie väiteid. Tõepoolest, korrutamise võime välja kirjutada järgmiselt:
Ning nagu jooniselt näeme, asub –1 + 3i täpselt 45-kraadise nurga all 1 + 2i suhtes, küll tõesti parasjagu nullpunktist kaugemal. See tuleneb lihtsalt sellest, et korrutamisel ei piisa ainult nurkade liitmisest, vaid tuleb omavahel korrutada ka kaugused.
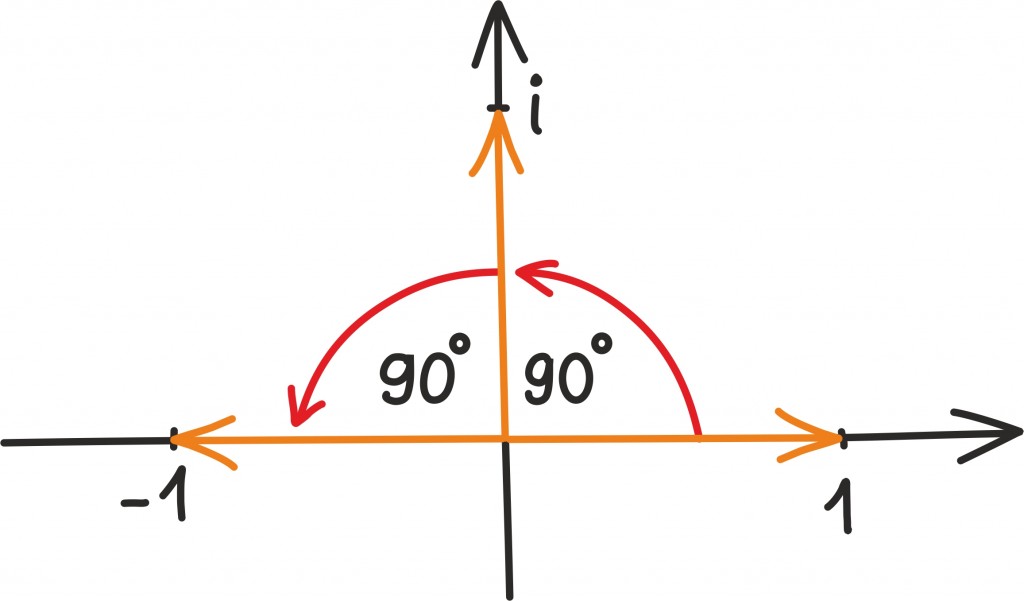
Imaginaararvuga korrutamisel on järelikult tegemist ainult pöördega 90° – tema kaugus nullist on ju täpselt 1 ühik. Nii liigub arv 1 arvuga i korrutamisel täpselt i-ks, arv 1 + i aga i-ga korrutamisel täpselt –1 + i-ks. See pakub ka arvuga –1 korrutamisele uue tõlgenduse: arvteljel oli –1 arvuga korrutamise tõlgenduseks peegeldus nullpunktist, nüüd aga teades, et –1 = i2, võime komplekstasandil arvuga –1 korrutamisest mõelda ka kui 180 kraadisest pöördest.