Avaldis. Võrrand
Avaldis
Avaldis on eeskiri, mis määrab tehted ja tehete sooritamise järjekorra.
Näiteid arvavaldistest.
2 + 3
3 · (7 – 3) + 2
Avaldisi, mis sisaldavad ka tähti, nimetatakse tähtavaldisteks.
Näiteid tähtavaldistest.
a + b
4 – a
Sulle võivad huvi pakkuda need õppematerjalid:
Funktsioonide graafikute lõikepunktide leidmine
Liitmine 20 piires
Tasandilised kujundid
xy-koordinaatsüsteem
Kirjalik liitmine
Harjutusülesandeid matemaatika riigieksamiks
Ratsionaalavaldised
Numbrilised seosed
Ruutjuur, tehted ruutjuurtega
Ruumilised kujundid
Ruutvõrrandi mõiste, ruutvõrrandi lahendivalem, ruutvõrrandi liigid
Ruutvõrrand
Üksliikmed, hulkliikmed ja tehted nendega
Kirjalik lahutamine
Liitmine ja lahutamine 20 piires
II kooliastme matemaatika reeglite kordamine
Liitmine 10 piires
Funktsioonide graafikud
Lahutamine 20 piires
Funktsioonid ja nende graafikud
Avaldise väärtus
Arvavaldise väärtuse leidmiseks tuleb teostada avaldises toodud tehted.
Näide 1.
Leiame avaldise 2 + 6 väärtuse.
2 + 6 = 8
Avaldise väärtus on 8.
Näide 2.
Leiame avaldise 4 · ( 2 + 3) : 2 väärtuse.
4 · (2 + 3) : 2 = 10
Avaldise väärtus on 10.
Võrdus
Võrduse moodustavad kaks võrdusmärgiga ühendatud avaldist.
Näiteid.
Järgnevad võrdused on arvvõrdused.
3 + 2 = 5
9 – 3 = 6
1 + 1 = 5 – 3
Järgnevad võrdused on tundmatut sisaldavad võrdused.
3 + a = 12 – 5
4 : b = 2
12 – 2 · m = 3 + 1
Tundmatut sisaldavat võrdust nimetatakse võrrandiks.
Võrdus võib olla tõene või väär.
Näiteid.
3 + 2 = 5 on tõene arvvõrdus.
6 + 1 = 2 on väär arvvõrdus.
Võrduse omadused näitavad, millal saadakse tõesest võrdusest tõene võrdus.
Võrrand
Võrrand on võrdus, mis sisaldab tundmatut.
Tundmatu leidmist võrrandist nimetatakse võrrandi lahendamiseks.
Võrrandist leitud tundmatu väärtus on võrrandi lahend.
Näide 1.
Võrrand on 6 + x = 10.
Võrrandi lahend x = 4, sest 6 + 4 = 10.
Võrrandit on lihtsam koostada, kui ülesande vormistamisel kirjutada iga tekstilõigu juurde vastav matemaatiline avaldis.
Näide 2.

Näide 3.
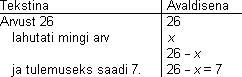
Võrratus
Võrratuse moodustavad kaks võrratusmärgiga ühendatud avaldist.
Võrratusmärgid on > (loetakse: on suurem) ja < (loetakse: on väiksem).
Näiteid võrratustest.
6 < 12
a > b
3 + 5 > a
Võrratusi lahendatakse selles kooliastmes põhiliselt proovimise teel, sest võrratuse omadusi ei ole veel tundma õpitud.




























