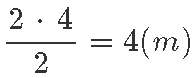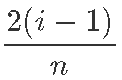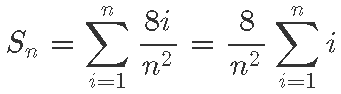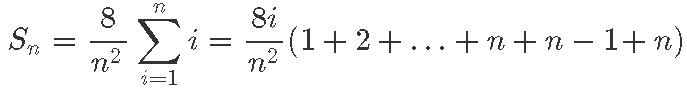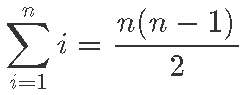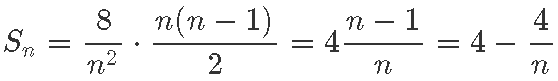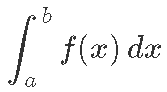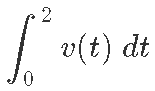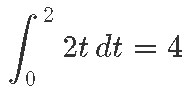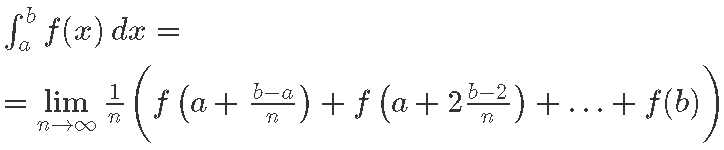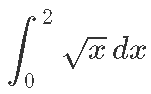Integraal
Pärast pikka talve on käes kevad, viskad suusad nurka ja asud rattaga ärkavat loodust avastama. Sõidad hoogsalt kodust eemale, kuid sooviksid siiski teada, kui kaugele oled jõudnud – jõudu peab ju jätkuma ka naasmiseks. Sul on võimalik igal hetkel näha ratta spidomeetri näitu ehk hetkekiirust. Kuidas saaksid leida kogu läbitud tee pikkuse?
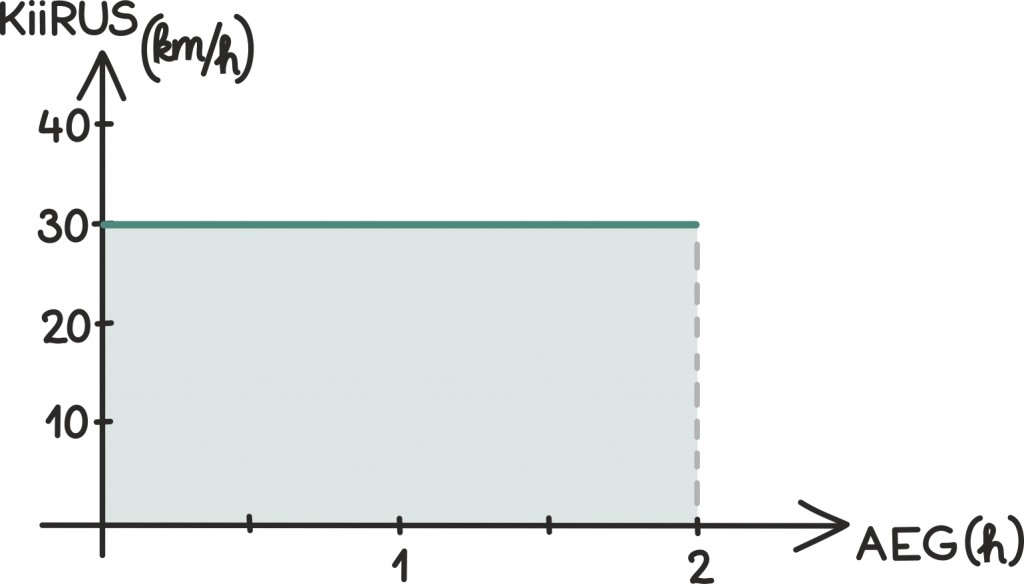
Kui sõidaksid esimesed kaks tundi muutumatu kiirusega 30 km/h, siis selle ajaga jõuaksid läbida 2 · 30 = 60 kilomeetrit. Seda võib ka graafiliselt kujutada, joonistades kiiruse sõltuvuse ajast. Sellel graafikul on esimese kahe tunniga läbitud tee pikkus antud täpselt kiiruse ning ajatelje vahele jääva ristküliku pindalaga:
Täpselt ühtlase kiirusega sõidetakse väga harva. Tegelikult muutub Su kiirus ilmselt peaaegu kogu aeg. Kuidas sellisel juhul leida läbitud tee pikkus?
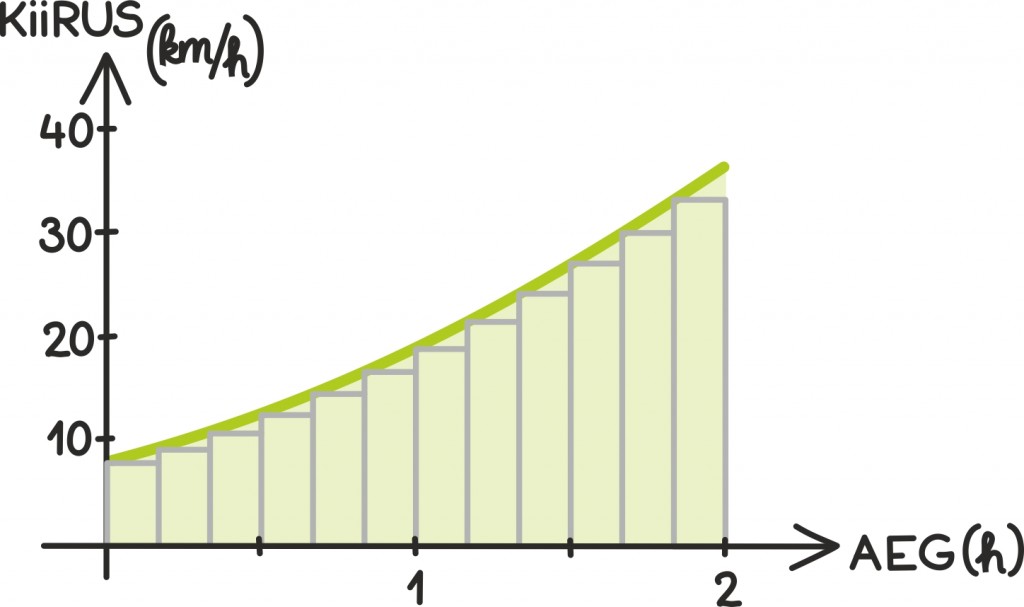
Ka seda olukorda võime kirjeldada graafiliselt, just nii nagu enne. Tuleb ka välja, et jällegi on läbitud tee pikkus antud kiiruse ning ajatelje vahele jääva piirkonna pindalaga. Läbitud tee pikkuse ehk funktsiooni graafiku alla jääva ala pindala aga annabki integraal.
Integreerimine
Kui tuletis oli ajast sõltuva funktsiooni spidomeetriks ning näitas funktsiooni hetkelist muutumise kiirust, siis integraali tähendus on vastupidine: integraal leiab funktsiooni spidomeetri põhjal tema kogumuudu. Järgnevalt alustame integraali idee selgitamisest ja loodame jõuda lõpuks siiski ka integraali matemaatilise definitsioonini [lk 44].
Sulle võivad huvi pakkuda need õppematerjalid:
Liitmine ja lahutamine 20 piires
Ruumilised kujundid
Tasandilised kujundid
Kell ja kellaaeg
Funktsioonide graafikud
Funktsioonide graafikute lõikepunktide leidmine
xy-koordinaatsüsteem
Funktsioonid ja nende graafikud
Peastarvutamine I kooliastmele
II kooliastme matemaatika reeglite kordamine
Ruutvõrrandi abil lahenduvad tekstülesanded
Ruutjuur, tehted ruutjuurtega
Liitmine 10 piires
Ratsionaalavaldised
Ruutvõrrandi mõiste, ruutvõrrandi lahendivalem, ruutvõrrandi liigid
Ruutvõrrand
Liitmine 20 piires
Harjutusülesandeid matemaatika riigieksamiks
Liitmine ja lahutamine 10 piires
Kirjalik lahutamine
Lugulaul
Kuna integraal ja tuletis on tihedalt seotud, alustame ka sarnase lugulauluga – kihutad mäest alla. Muidugi, nagu sissejuhatuses juba mainisime, on nüüd käes kevad ning suuskade asemel oleme andnud Sulle hoopis ratta. Lisaks on meil seekord käepärast spidomeeter ja tahame arvutada hoopis läbitud tee pikkust.
Kuidas seda teha? Oskame tee pikkust kiiruse ja aja abil leida siis, kui kiirus on konstantne. Sellisel juhul on ka kiiruse graafiku alla jääv kujund kenasti ristkülik ning pindala valem ühtib täpselt tee pikkuse leidmise valemiga: s = vt
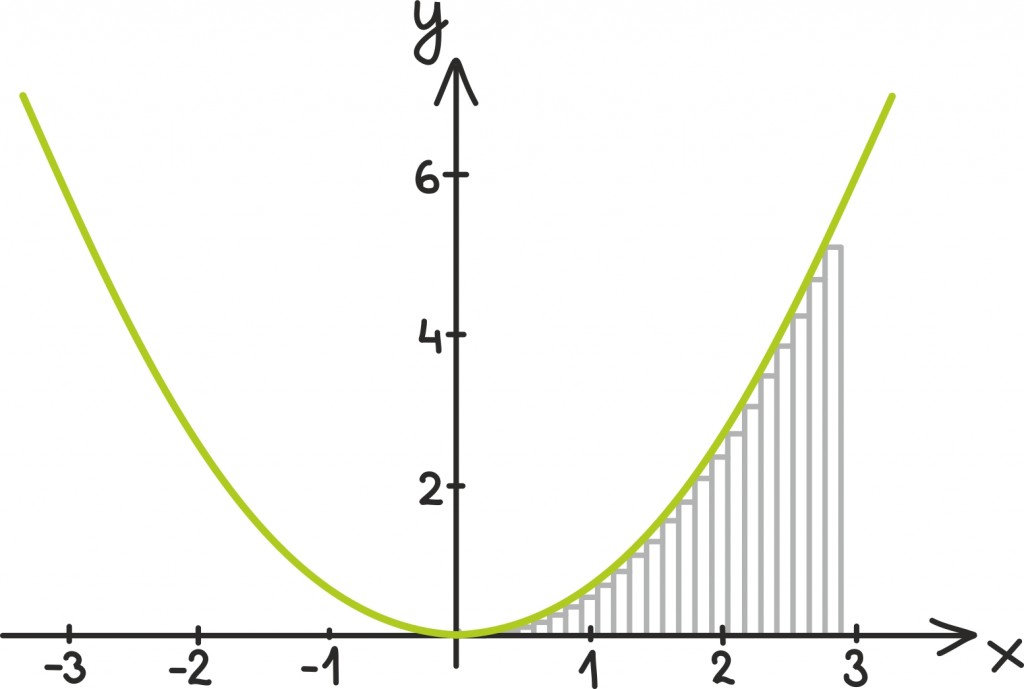
Probleem on aga selles, et mäest alla veeredes kiirus aina suureneb. Seega kümnendaks sekundiks läbitud tee pikkuse leidmiseks ei piisa enam sellest, kui vaataksime spidomeetrit näiteks alles viimasel sekundil ning kasutaksime seda kiirust oma läbitud tee pikkuse leidmiseks. Probleemi lahendus on siiski üsna lihtne: jagame aja lühikesteks vahemikeks ehk vaatame spidomeetrit üsna tihedalt.
Idee peitub selles, et väga lühikese ajavahemiku jooksul kiirus väga ei muutu. Seega võime igas lühikeses ajavahemikus läbitud tee pikkuse leida üsna täpselt, kui korrutame lihtsalt ajavahemiku pikkuse ning spidomeetrilt saadud kiiruse. Liites seejärel kokku igas lühikeses ajavahemikus läbitud tee pikkused, saamegi päris täpse vastuse.
Nagu tuletisegi peatükis – mida väiksemad ajavahemikud võtame ehk mida tihedamalt spidomeetrit vaatame, seda täpsem on ka meie vastus. Seekord annab integraal selle täpse vastuse, mida otsime – täpse tee pikkuse – ja taas kord tulevad matemaatiliselt mängu ka piirprotsessid [lk 308]. Nagu hiljem näeme, on nad seekord ainult veidi keerulisemad kirja panna.
Kõike seda võib ette kujutada ka geomeetriliselt.
Esiteks, aja lühikesteks vahemikeks jagamine tähendab geomeetriliselt lihtsalt kiiruse graafiku alla jääva kujundi jagamist väikesteks tükkideks.
Teiseks, igas vahemikus tavalise teepikkuse valemi kasutamine tähendab, et iga väikese tüki pindala lähendame ristkülikukujulise tüki pindalaga.
Lõpuks liidame kõik need pindalad kokku.
Joonist lähemalt vaadates on üsna selge, et mida väiksemad ajavahemikud, seda täpsem vastus. Kasutades ristkülikutega lähendamist, teeme iga väikese pindala arvutamisel teatava vea, aga mida väiksem vahemik, seda vähem oma hinnangus eksime.
Seega kokkuvõttes, täpne läbitud tee pikkus ongi kiirusfunktsiooni integraal ning omakorda on see antud kiirusfunktsiooni alla jääva kõvertrapetsi (nii nad seda kutsuvad…) pindalaga.
Taas kord on praktikas, spidomeetri abil täpse tee pikkuse ehk integraali leidmine võimatu – lõpmatult tihedalt ei ole võimalik spidomeetrit vaadata. Niipea kui meil on käest võtta matemaatiline kirjeldus, saame aga kohe asuda integreerima.
Konkreetne näide
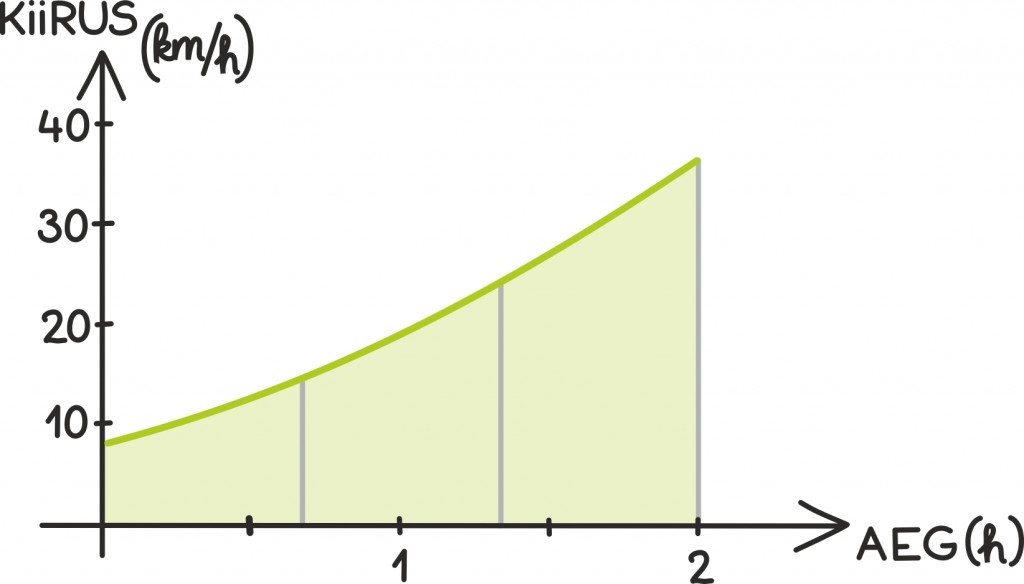
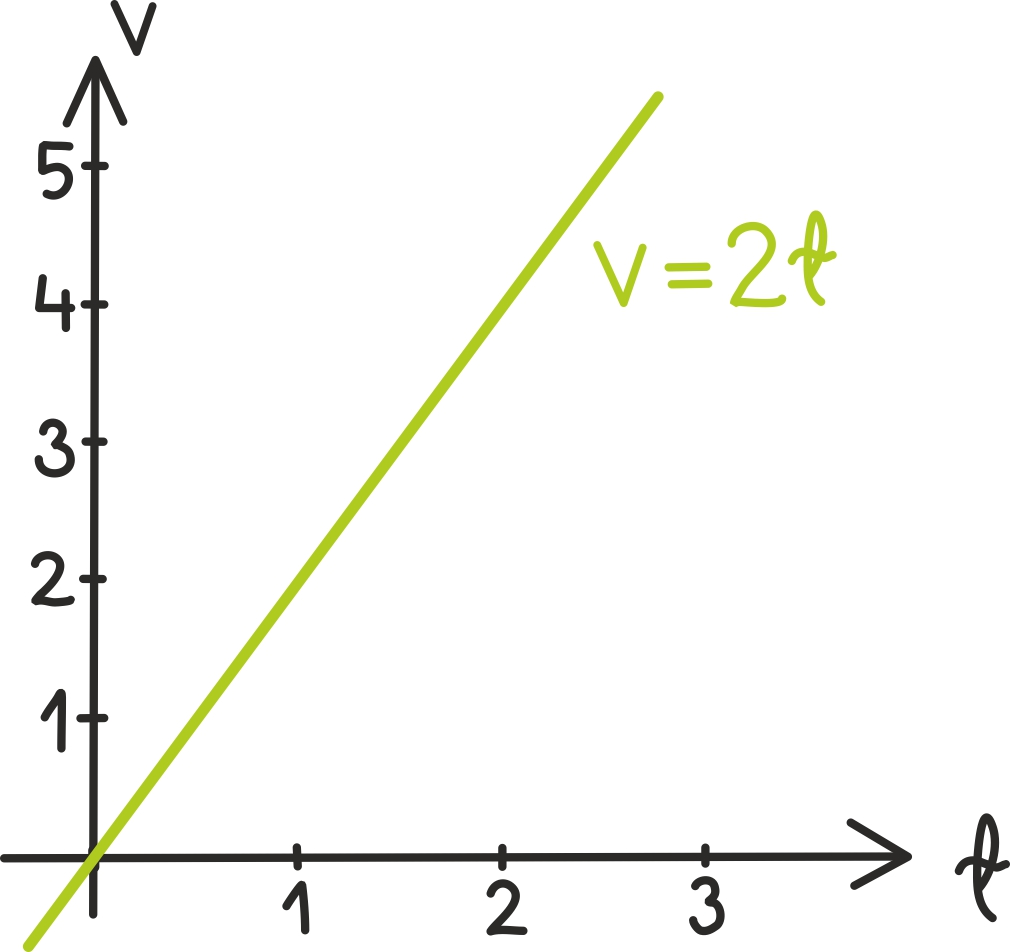
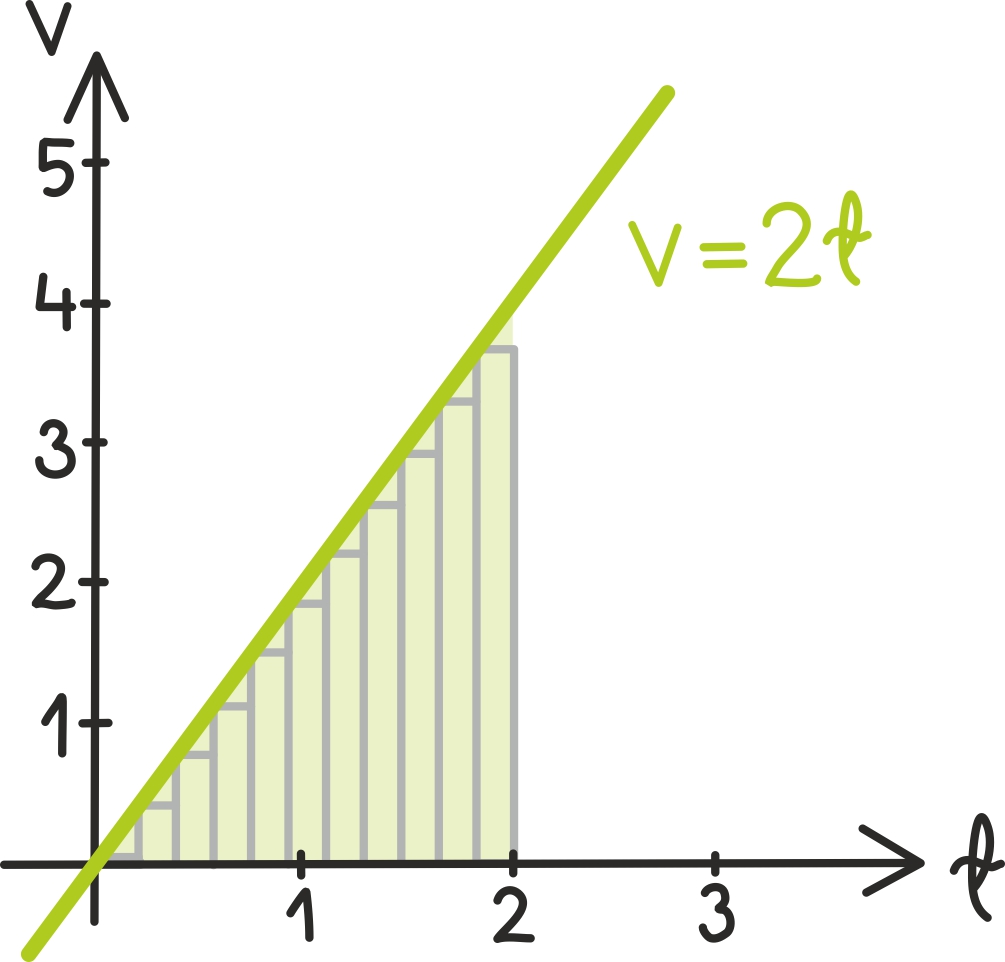
Täpsustame nüüd, et tuiskad rattaga jällegi alla meile juba tuntud ideaalsest mäest. Tuletame meelde ka tuletise peatükist, et sel juhul on Su kiirus ajas antud valemiga v = 2t. Kuna laskumised pole väga pikad, mõõdame jälle aega sekundites.
Nagu juba märkasime, võime kiiruse ja aja suhet kirjeldada graafiliselt:
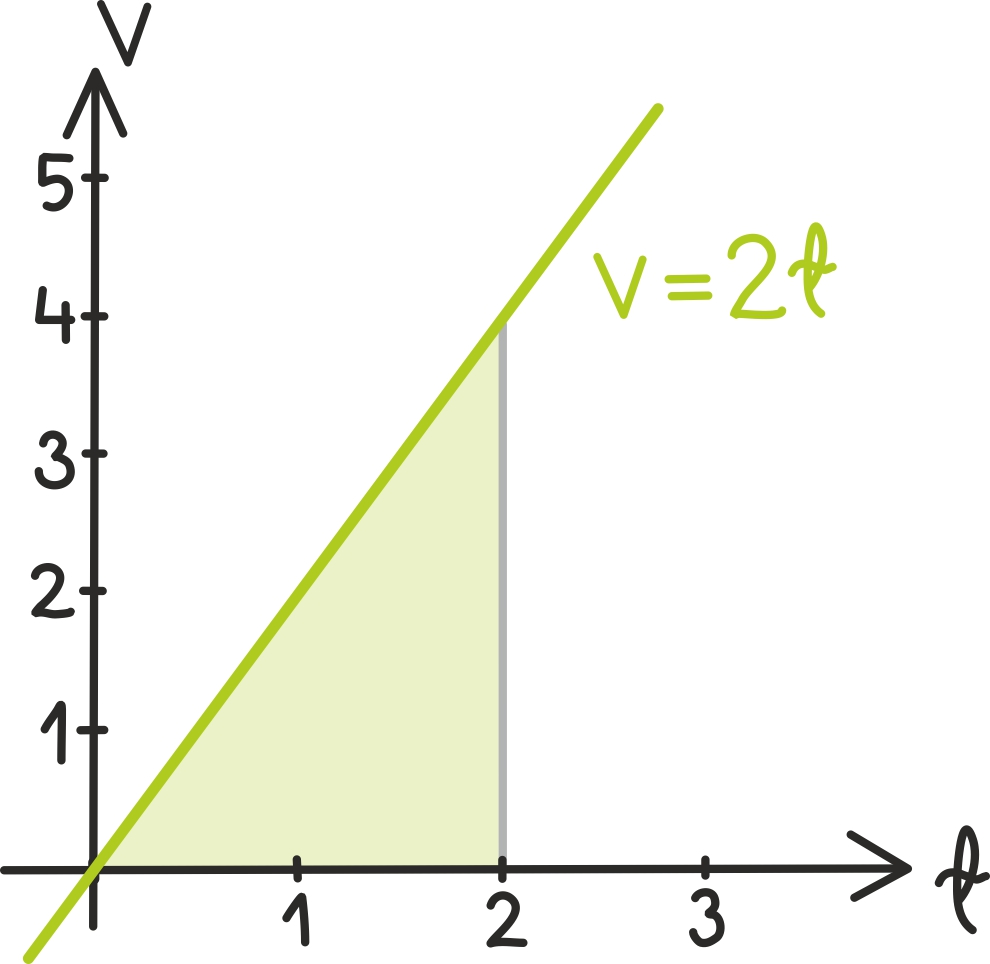
Nii on kahe sekundi möödudes juba saavutatud kiirus 4 m/s. Kui tahame nüüd leida nende kahe sekundiga läbitud tee pikkust, peame lihtsalt leidma joone alla jääva kujundi pindala.
Kavalpead võivad kohe näha, et võime seda teha näiteks kolmnurga pindala valemist ning saada vastuseks
Teine ning levinuim viis selle integraali leidmiseks on kasutada seost tuletise ja integraali vahel – kuna integraal ja tuletis on teatud mõttes pöördoperatsioonid, võime integraali leidmise taandada tuletise teadmisele ning vastupidi. Sellest pikemalt integraali ja tuletise peatükis [lk 352].
Viimaks näitame aga, kuidas integraali leida näppudel, kiiruse graafiku alla jäävat kujundit väikesteks tükkideks jagades ning nende pindalasid kokku liites, ehk lühemalt – kuidas käsitsi integreerida:
Jagame oma lühikese ajavahemiku 2 sekundit n väikeseks vahemikuks, millest iga pikkus on täpselt
Vahemik i ulatub siis ajahetkest
kuni ajahetkeni
Igas selles vahemikus hindame kiirust vahemiku lõppkiiruse abil.
Kasutades valemit v = 2t, on meie hinnang vahemiku i lõppkiiruse jaoks
Selles vahemikus läbitakse seega hinnanguliselt tee pikkus
Liites need väikesed tee pikkused kokku, saame
See kõverik on juba varem kirjeldatud [lk 50] summa märk, aga meeldetuletuseks kirjutame summa ka pikalt välja:
Me juba teame (näiteks aritmeetilise jada summavalemist), et
seega
Meie hinnang sõltub selgelt ajavahemike arvust n liikme
kaudu.
Samas kui n viia lõpmatult suureks, muutub see liige imepisikeseks ning piirprotsessis kaob hoopis. Seega saame kogu tee pikkuseks ehk integraaliks vastuse 4. Ühikud tuleks muidugi eraldi juurde sobitada, et saada nagu enne vastus 4 meetrit.
Integraali tähis ja matemaatiline kirjapanek
Matemaatilisemaks kirjelduseks on kunstilembesed matemaatikud integraalile andnud ka tähise, mis on lihtsalt üks välja venitatud s.
S on ta just sellepärast, et integraal ise on lõputult paljude asjade kokkuliitmisel justkui üks välja venitatud summa.
Sellises kõverikus endas on aga veel üsna vähe informatsiooni. Et teda mõistlikult kasutada, on veel vaja ära märkida, mida me integreerime, mille suhtes ja kui pikas vahemikus.
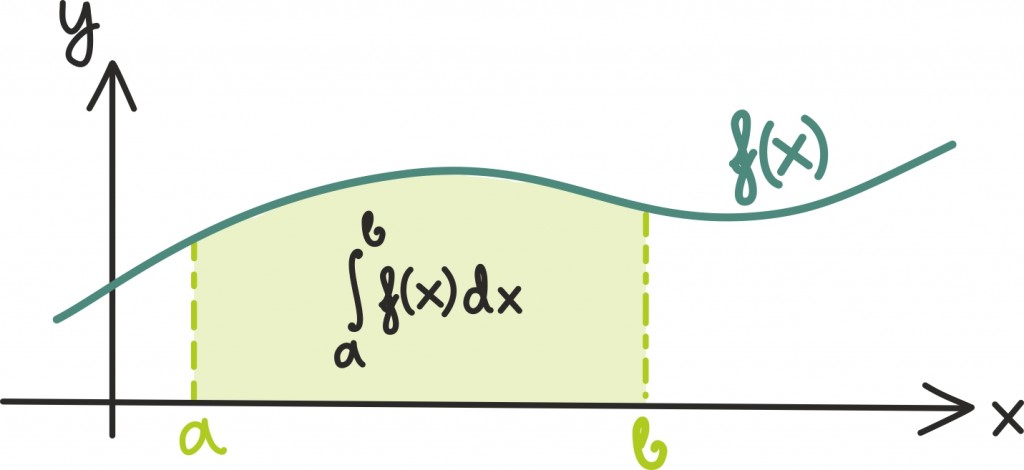
Kui meil on antud mingi muutumist kirjeldav funktsioon ƒ(x), siis tema integraali või kogumuutust x-i suhtes vahemikus [a, b] tähistame:
Graafiliselt on see integraal vastavuses siis x-telje, joonte x = a ning x = b ja funktsiooni ƒ(x) graafiku vahele jääva piirkonna pindalaga:
Ülaltoodud näites integreerime kiirust v(t) aja t suhtes, vahemikus ajahetkest 0 kuni ajahetkeni 2, sel juhul võime integraali kirja panna kujus:
Meie konkreetse näite korral leidsime siis järgmise integraali:
Kuhu jääb definitsioon?
Aga kuhu jääb integraali matemaatiline definitsioon?
Lihtne vastus: suur osa täpsest definitsioonist jääb ülikooli. Integraali mõistlikuks defineerimiseks tuleb olla päris hoolas.
Tuletame meelde, et integraal mõõtis spidomeetri põhjal tee pikkuse kogumuutu mingis vahemikus. Tema leidmiseks jagasime ahemiku väikesteks tükkideks ning leidsime muudu neis vahemikes. Liites need muudud kokku, saime hinnangu integraalile. Piirprotsessis, kus vahemikke oli aina rohkem ning nad olid aina lühemad, saimegi integraali enda.
Konkreetses näites kasutasime tee pikkuse leidmiseks ühepikkuseid ajavahemikke ning mõõtsime igas vahemikus kiirust ajavahemiku otspunkti põhjal.
Võttes sellest kõigest malli, võiksime matemaatiliselt defineerida, et integraal tähendab just seda, et jagame ajavahemiku järjest rohkemateks osadeks, valime alati pisikeste ajavahemike otspunktid ning arvestame neid tee pikkuse leidmiseks. Integraali saame piirprotsessis, kus n tormab lõpmatusse.
Sümbolite keelde tõlkides tähendaks see, et defineeriksime:
Ent stopp! Siin teeme kaks üsna suvalist valikut. Esiteks on suvaline see, et jagame kogu vahemiku võrdseteks tükkideks. Teiseks, miks peaksime muutu hindama just vahemiku parema otspunkti põhjal?
Ühtegi väga head põhjust kummakski ei ole ja see peaks juba valvsaks tegema – kas me tegime õiged valikud? Kas teised valikud annaksid ikka sama integraali? Kas leidub mõni „õige” valik? Kas saab kuidagi üldisemalt integraali defineerida, nii et ei täpsustagi täpselt, kuidas vahemikke võtame ning millise punkti neis valime?
Kõik need on põnevad küsimused, kahjuks jäävad aga sellest raamatust juba kaugemale. Integraali rangeks defineerimiseks leidubki tegelikult mitu erinevat viisi intuitsiooni jääb aga alati samaks, selleks, mille ülalpool ka esile tõime. Kusjuures võibolla on ka oluline lisada, et konkreetsed siin tehtud valikud pole just parimad – neid kasutades võime integreerida ainult üsna ilusaid funktsioone, kõik keerulisem toob juba kaasa probleeme.
Integraal ja üldisemad pindalad
Arutlesime, et integraalist võib mõelda ka kui mingi kindla joone ja x-telje vahele jääva ala pindalast. Tegelikult võime pisut kavaldades leida integreerimise abil ka paljude teiste kujundite pindalad.
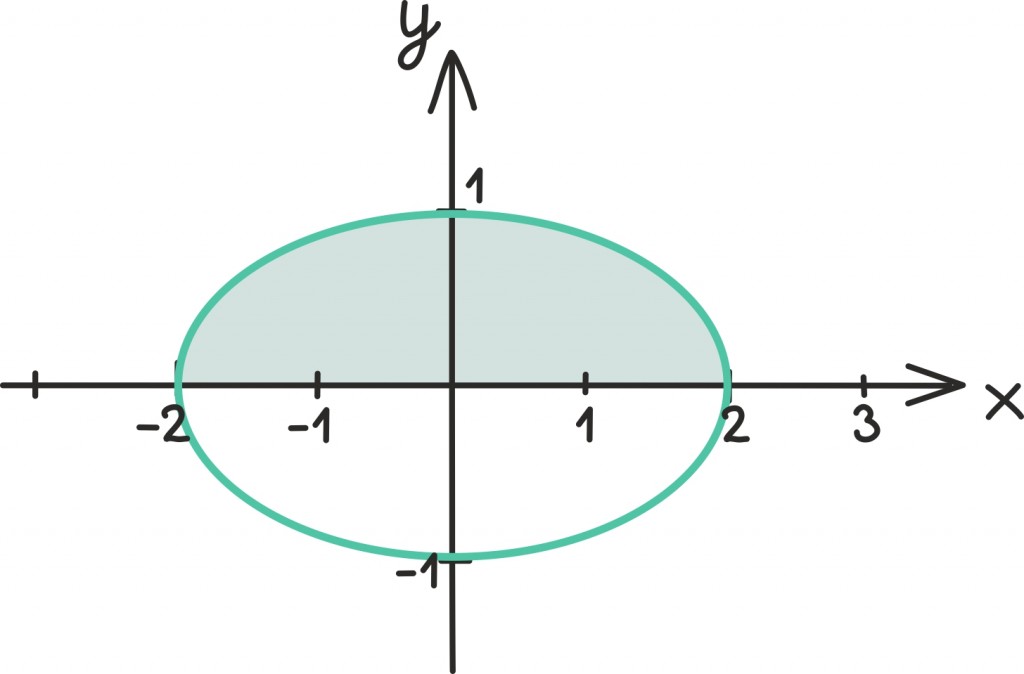
Üks viis kavaldada polegi nii väga keeruline. Vaatame näiteks üht kena väljavenitatud ringjoont ehk ellipsit.
Kuidas integraali abil selle ellipsi pindala leida? Esiteks peame ta muidugi asetama koordinaatteljestikule. Nagu näeme, tekib siis tegelikult kaks kaart – ülemine ja alumine –, mida mõlemat võiksime vaadata funktsioonina x-st:
Leides ülemise kaare integraali, saame vastuseks ellipsi ülemise osa pindala. Aga ellips on ju kenasti sümmeetriline ja nii võime saadu lihtsalt kahega korrutada ning saadagi kogupindala!
Üldisemalt, isegi kui kena sümmeetriat abiks pole, võime mõne kõvera kujundi pindala leidmiseks jagada kujundi horisontaalteljega kaheks, leida ülemise ja alumise kaare integraalid ning lõpuks lahutada ülemise kaare integraalist alumise kaare integraali. Lahutama peame seetõttu, et alumise kaare integraal annab meile negatiivse vastuse – allpool x-telge asuv osa tähendab ju negatiivset muutu.
See pole aga kõik! Tegelikult ei ole alati loomulikjagada kujundit just ristkülikute abil tükkideks. Näiteks ringi pindala leidmiseks võiksime ta ju jagada hoopis väikesteks rõngasteks ning seeläbi leida ringi pindala. Sellest aga pikemalt juba pindalade peatükis [lk 367].
Viimaks ei ole muidugi mingit põhjust piirduda ainult pindalade ehk kahemõõtmeliste mahtudega. Integreerimist võime kasutada ka näiteks ruumalade leidmiseks. Osas 8 leiamegi sel viisil näiteks kera ruumala valemi [lk 375].
Kuidas integreerib arvuti
Eluliste ülesannetega maadeldes kohtame vahel ka funktsioone, mille integreerimine on paras piin. Ei saa nende integraali leida mõne kavala pindala valemiga ega ole abi ka seosest tuletisega – me lihtsalt ei tea, millise funktsiooni tuletiseks nad on. Nii peame määramata integraali leidma käsitsi integreerimisega.
Päris käsitsi oleks see muidugi paras õudus, ent õnneks on meil tänapäeval olemas arvutid, kes oskavad teha miljoneid väikseid tehteid sekundis. Nii võime eeltoodud mooduse integraali leidmiseks – jagada piirkond paljudeks vahemikeks, leida muut igas vahemikus ning need muudud kokku liita – arvutile selgeks teha.
Näiteks võime lasta arvutil jagada integreerimisvahemiku miljoniks võrdseks osaks, leida nende osade pikkused ning kogumuudud ja arvutadagi lähenduse integraalile.
Muidugi saame seeläbi alati natuke ebatäpse väärtuse, ent samas võime selle ebatäpsuse teha nii väikseks kui vähegi soovime.
See viis ei ole aga integraalide arvutamiseks kõige efektiivsem ning praeguseks on välja arendatud kümneid algoritme, mis on täpsemad, usaldusväärsemad ja efektiivsemad.
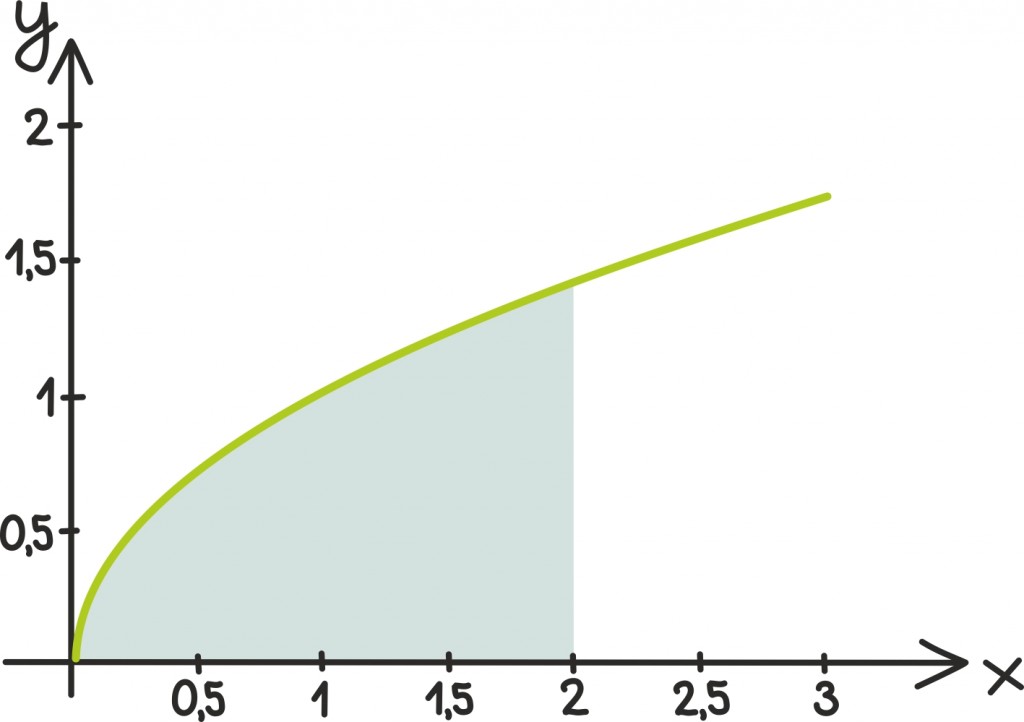
Näiteks väga mitmemõõtmeliste ja keeruliste funktsioonide puhul osutub vahel kõige paremaks algoritmiks niinimetatud Monte Carlo meetod. Tutvustame seda lihtsa näitega: oletame, et soovime leida väärtuse integraalile
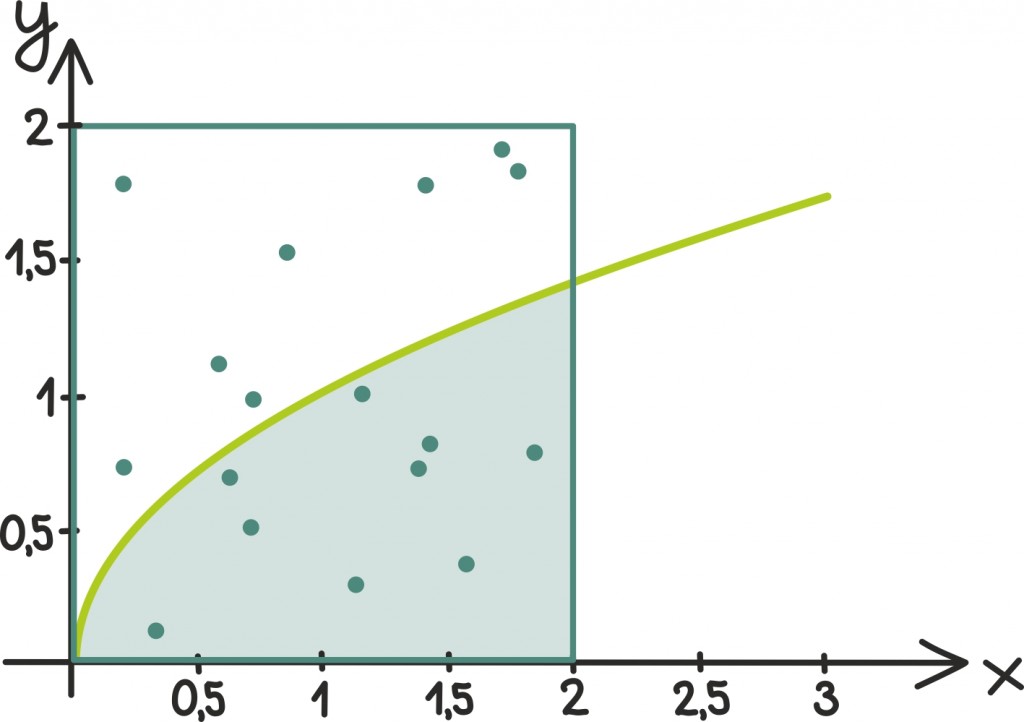
Monte Carlo meetodi idee on kasutada niinimetatud geomeetrilist tõenäosust: [lk 402] kui me võtaksime mõne juhusliku arvu ruudust [0; 2] × [0; 2], siis tõenäosus, et ta jääb funktsiooni √x graafiku alla, on täpselt võrdne graafiku alla jääva pindala ning kogupindala suhtega.
Edasi on meil vaja lihtsalt juhuslikke arve genereerida ning seda tõenäosust hinnata. Sobivate juhuslike arvude genereerimine on aga üsna vähenõudev ning samuti on kiire ka kontrollimine, kas arv jääb funktsiooni graafiku alla. Nii saamegi ühe üsna efektiivse meetodi integraalide ligikaudseks arvutamiseks. Seekord on meie vastus seda täpsem, mida rohkem juhuslikke arve kasutame.