SARNASED KOLMNURGAD JA SARNASUSE TUNNUSED
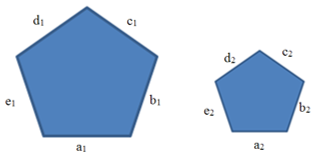
Hulknurkade sarnasus: kaht hulknurka nimetatakse teineteisega sarnasteks, kui nende hulknurkade vastavad nurgad on võrdsed ja küljed on võrdelised. Sarnaste hulknurkade vastavate külgede jagatist nimetatakse sarnasusteguriks.
Ülevaloleval joonisel on kaks sarnast viisnurka. Vastavate külgede suhted on võrdelised ehk 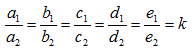 , kus arv k on võrdetegur.
, kus arv k on võrdetegur.
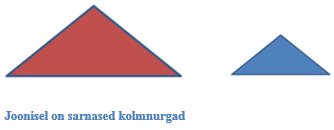
Kaks kolmnurka on teineteisega sarnased, kui nende vastavad nurgad on võrdsed ja küljed on võrdelised.
Kolmnurkade sarnasuse tunnused:
Sulle võivad huvi pakkuda need õppematerjalid:
Kirjalik liitmine
xy-koordinaatsüsteem
Ruutjuur, tehted ruutjuurtega
Funktsioonide graafikud
II kooliastme matemaatika reeglite kordamine
Algebralised murrud
Harjutusülesandeid matemaatika riigieksamiks
8. klassi matemaatika teooriavideod
Ratsionaalavaldised
Üksliikmed, hulkliikmed ja tehted nendega
Funktsioonide graafikute lõikepunktide leidmine
Liitmine ja lahutamine 10 piires
Peastarvutamine eelkoolile
Numbrilised seosed
Ruumilised kujundid
Hariliku murru kordamine
Liitmine ja lahutamine 20 piires
Ruutvõrrandi mõiste, ruutvõrrandi lahendivalem, ruutvõrrandi liigid
Liitmine 20 piires
Peastarvutamine I kooliastmele
- Kaks kolmnurka on sarnased, kui ühe kolmnurga kolm külge on võrdelised teise kolmnurga vastavate külgedega (sarnasuse tunnus KKK ehk külg-külg-külg)
- Kaks kolmnurka on sarnased, kui ühe kolmnurga kaks külge on võrdelised teise kolmnurga kahe küljega ja nende külgede vahelised nurgad on võrdsed (sarnasuse tunnus KNK ehk külg-nurk-külg)
- Kaks kolmnurka on sarnased, kui ühe kolmnurga kaks nurka on vastavalt võrdsed teise kolmnurga kahe nurgaga (sarnasuse tunnus NN ehk nurk-nurk)
Ka sarnaste kolmnurkade vastavad küljed on võrdelised.
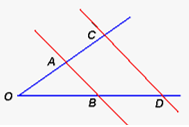
Kiirteteoreem: kui nurga haarasid lõigata paralleelsete sirgetega, siis nurga ühel haaral tekkinud lõigud on võrdelised teise haara lõikudega st et ![]()
Sellest saab teha järelduse, et kui nurga haarasid lõigata paralleelsete sirgetega, tekivad võrdeliste külgedega kolmnurgad ehk ![]() ja nende küljed on võrdelised
ja nende küljed on võrdelised ![]() .
.
Kiirteteoreemi pöördteoreem: kui sirged lõikavad nurga haarasid nii, et ühel haaral tekkinud lõigud on võrdelised teisel haaral tekkinud lõikudega, siis on need lõikesirged paralleelsed.
Kiirteteoreem, sarnased kolmnurgad: