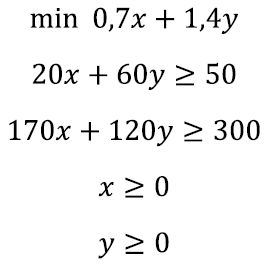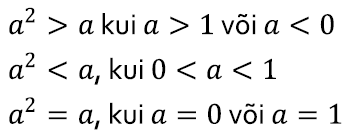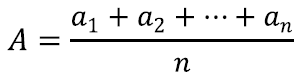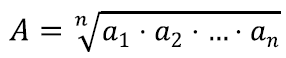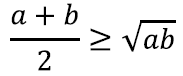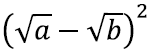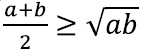Võrratus
Võrratuste koostamine
Nagu võrrandi korralgi, koostame ka võrratusi tihti mõne elulise situatsiooni kirjeldamiseks või mõne elulise küsimuse lahendamiseks. Võrratuste ja võrrandite koostamine on väga sarnane – seame elulistele suurustele vastavusse muutujad ja määrame nendevahelised suhted.
- operaator A: 5 eurot kuumakse pluss 0,01 eurot kõneminut,
- operaator B: 1 eurot kuumakse pluss 0,02 eurot kõneminut
Võrrandi peatükis küsisime, kui palju peaksime telefoniga rääkima, et operaatorite juures oleksid kuutasud võrdsed. Kuna on aga selge, et operaator A muutub soodsamaks, kui räägime palju, oleks loomulikum küsida: kui palju peaksime telefoniga rääkima, et operaator A muutuks soodsamaks?
Kuna kuutasu sõltub mõlemal juhul otseselt räägitud kõneminutite arvust, tuleb ta kindlasti mängu tuua ning võime ta tähistada näiteks muutujaga k. Seega võime kuutasud välja kirjutada järgmiselt:
- Operaator A juures: 5 + 0,01k eurot
- Operaator B juures: 1 + 0,02k eurot
Meie küsimust, millal on operaator A kuutasu odavam, esitab siis täpselt võrratus:
Nagu võrranditegi korral, on võrratuses endas nüüd kontekst kadunud: küsime lihtsalt, milliste k-de korral on vasem pool väiksem paremast. Pärast võime vastuse tõlkida jälle elukeelde ja vastatagi, milliste kuuminutite arvu korral on operaator A pakett odavam.
Nüüd räägimegi võrratuste lahendamisest lähemalt.
Sulle võivad huvi pakkuda need õppematerjalid:
II kooliastme matemaatika reeglite kordamine
Üksliikmed, hulkliikmed ja tehted nendega
Lahutamine 20 piires
Liitmine ja lahutamine 10 piires
Peastarvutamine I kooliastmele
Kell ja kellaaeg
Tasandilised kujundid
Kirjalik lahutamine
Numbrilised seosed
Funktsioonide graafikute lõikepunktide leidmine
Ruutvõrrandi mõiste, ruutvõrrandi lahendivalem, ruutvõrrandi liigid
xy-koordinaatsüsteem
Peastarvutamine eelkoolile
Funktsioonide graafikud
Liitmine 20 piires
Ruutvõrrandi abil lahenduvad tekstülesanded
Ruutvõrrand
Ruutjuur, tehted ruutjuurtega
Harjutusülesandeid matemaatika riigieksamiks
Liitmine ja lahutamine 20 piires
Võrratuste lahendamine
Võrratuse lahendamine tähendab täpselt sama, mida võrrandi lahendaminegi – tuleb leida antud tingimustega sobivad muutuja väärtused [lk 176].
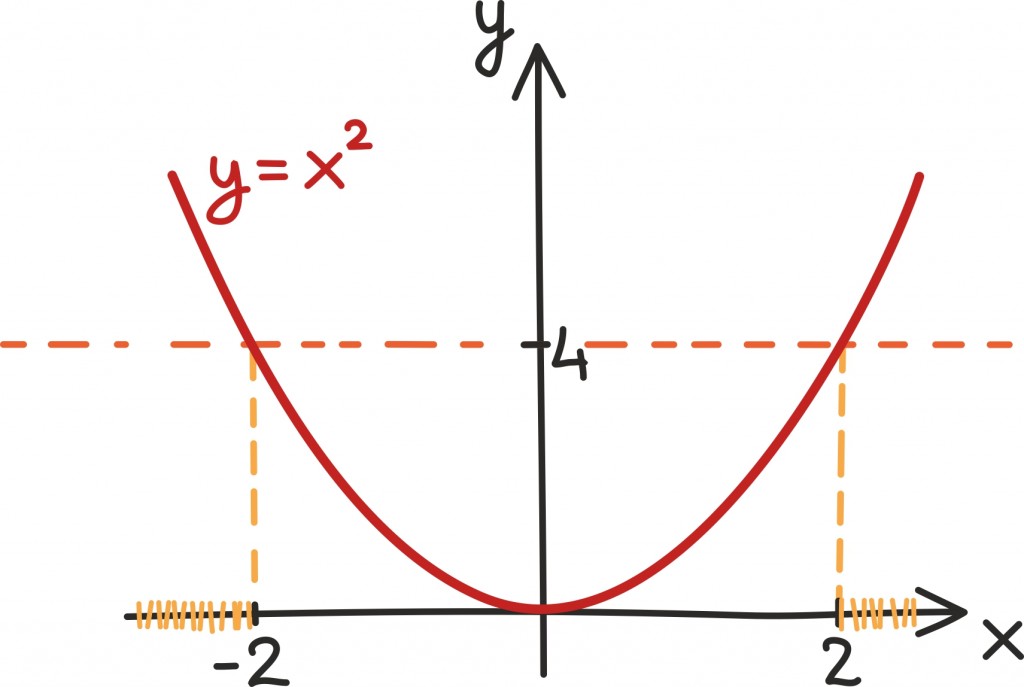
Näiteks kui tahtsime leida arve, mille ruut oli võrdne 4-ga, saime võrrandi: x2 = 4. Samamoodi võime otsida arve, mille arvuruut on 4-st suurem. Seda kirjeldab võrratus: x2 > 4.
Võrratuste lahendamisel on tihti kasulik mõelda geomeetriliselt – üritame kogu võrratuse taandada mõne funktsiooni graafiku uurimisele.
Ülaltoodud võrratuse korral näeme, et kõik otsitavad arvud peavad olema kas kahest suuremad või miinus kahest väiksemad, sest muudel juhtudel on ruutfunktsiooni y = x2 graafik 4-st madalamal.
Sama strateegia toimib ka keerulisemate võrratuste puhul. Näiteks oletame, et küsitakse, milliste reaalarvude x jaoks on
Kasutades võrratuse omadusi võime selle võrratuse ümber viia kujusse
Sellises kujus vastab võrratus küsimusele: millal asub kuupfunktsioon x-teljest üleval pool?
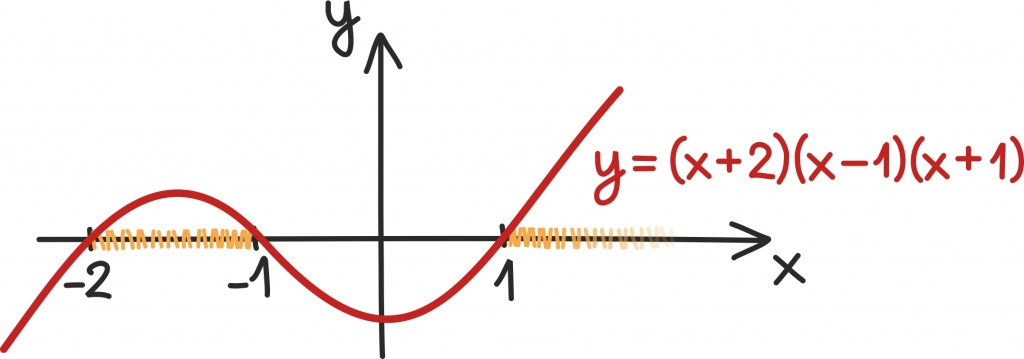
Kuupfunktsiooni graafik teeb kokku maksimaalselt kaks pööret, aga sellest räägime pikemalt osa 6 juures [lk 266].
Kuupfunktsiooni oskame umbkaudu joonistada niipea, kui teame ta nullkohti [lk 269]. Seega tegurdame vasemat poolt ja saame samaväärse võrratuse (x + 2) (x – 1) (x + 1) > 0. Nüüd võime vastuse välja lugeda joonistades umbkaudselt kuupfunktsiooni y = (x + 2) (x – 1) (x + 1) graafiku.
Meile sobivad kõik arvud vahemikus (–2, –1) ning kõik ühest suuremad arvud:
Graafiline meetod põhineb sisuliselt funktsioonide graafikute võrdlemisel. Oleksime võinud eelnevalt ka lihtsalt võrrelda funktsioonide x3 + 2x2 ja x + 2 graafikuid, aga lihtsam oli teisendada võrratust nii, et üks funktsioon oli kuuppolünoom ja teine lihtne nullfunktsiooni, mille graafikuks on siis x-telg ise.
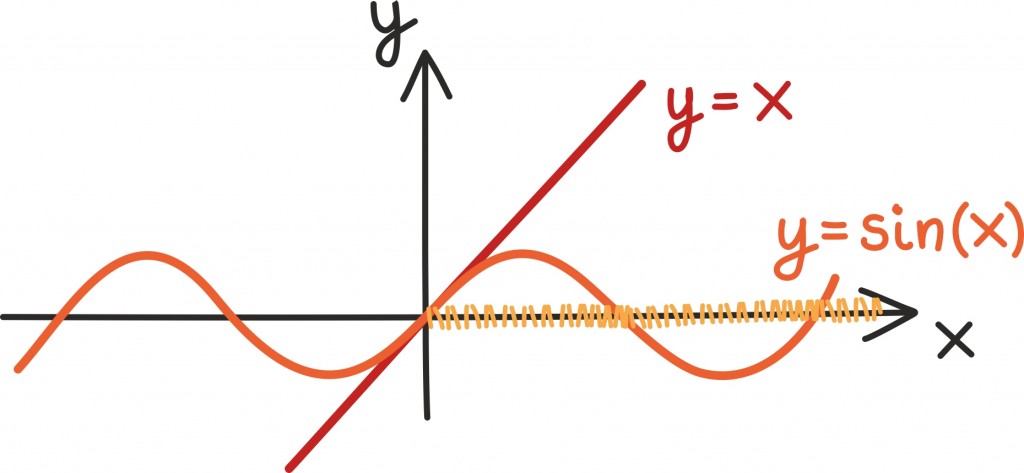
Mõnikord peame aga tõesti joonistama välja kaks erinevat funktsiooni. Näiteks näeme graafikult, et x ≥sin(x) iga mittenegatiivse x-i jaoks.
Selle fakti range tõestus kasutab tuletist [lk 320] ja põhineb täpselt graafikult saadud intuitsioonil: kohal 0 on mõlemad funktsioonid võrdsed ning edasi kasvab funktsioon y = x kiiremini kui funktsioon y = sin(x).
Võrratuste teisendamine
Võrratustega võib teha peaaegu kõike, mis võrranditegagi. Samaväärsed võrratused saame näiteks, kui
- liidame mõlemale võrratuse poolele sama arvu juurde. See on ju igati intuitiivne – kui Sul on rohkem raamatuid kui vennal, on Sul neid rohkem ka pärast seda, kui kirjandushuviline tädi mõlemale teile uue raamatu kingib;
- korrutame võrratuse mõlemat poolt sama positiivse arvuga. Ka see on loomulik: perepitsa on suurem kui tavaline pitsa ning ka pool või neljandik perepitsat on suurem kui pool või neljandik tavalisest pitsast.
Siinkohal on oluline märgata, et mõlemaid pooli võib ainult positiivse arvuga läbi korrutada ja mitte negatiivse arvuga. Negatiivse arvu korral tuleb võrratuse märk muuta vastupidiseks. Miks see nii on?
Alustame ühest näitest, võrratusest –3 < 2. Kui mõlemad pooled korrutada läbi –1-ga, saame arvudeks vastavalt 3 ja –2. Kuid enam ei ole 3 väiksem kui 2. Selle välistamiseks pöörame märgi vastupidiseks ning saame, et 3 > –2.
Tähendab ju mõlema võrratuse poole miinus ühega läbi korrutamine tegelikult arvtelje peegeldust 0 punkti suhtes ja nii muutubki võrratuse märk – suurus, mis enne oli arvteljel kõige paremal ning seega suurim, asub pärast peegeldust kõige vasemal ning on seega väikseim.
Võrratused ja planeerimine
Matemaatiline planeerimine tegeleb teatud mõttes elulistele probleemidele parimate lahenduste leidmisega. Seejuures on võrratustel matemaatilises planeerimises oluline osa. Toome mõned näited.
- Kuidas peaks bussifirma korraldama bussiliiklust, nii et teenida võimalikult palju kasumit? Ühelt poolt tahab bussifirma teha võimalikult vähe kulutusi bussijuhtidele, bussidele ja kütusele. Teiselt poolt peab ta pakkuma võimalikult head teenust, et reisijad ei läheks konkurentide juurde või ei hakkaks sõitma autoga.
- Milline on parim istekohtade jaotus klassiruumis, et õpilased oleksid võimalikult õnnelikud? Arvesse tuleb võtta nii õpilaste istekoha- kui ka pinginaabrite eelistusi.
- Mida peaks vaene üliõpilane sööma nii, et ta kulutused toidule oleksid võimalikult väiksed, kuid päevased toitainete normid oleksid täidetud?
Järgnevalt vaatame viimast probleemi lähemalt üsna lihtsustatud näite varal, kus tudengi ostukorvi saavad kuuluda vaid kartulid ja oad. Peab tõdema, et päriselt ei taha küll vist keegi ainult kartulitest ja ubadest toituda, aga realistlikumad probleemid on liiga keerulised, et neid paberil ilma arvutite abita lahendada.
Igal juhul alustame oma teadmiste ülesloetlemisega.
- Kilo kartuleid maksab 0,7 eurot, sisaldab 20g valke ning 170g süsivesikuid.
- Kilo ubasid tomatikastmes maksab 1,4 eurot, sisaldab 60g valke ja 120g süsivesikuid.
- Täiskasvanud inimene vajab 50g valke ja 300g süsivesikuid.
Meie küsimus on, millise toidurahaga saab vaene tudeng päevas hakkama ainult kartuleid ja ubasid süües, nii et päeva valkude ja süsivesikute norm oleks täidetud?
Kõigepealt peame selle ülesande tõlkima matemaatika keelde ehk koostama matemaatilise mudeli.
Esmalt leiame koguhinna. Selle jaoks tähistame kartulite kogust kilodes x-iga ning ubade kogust kilodes y-iga. Nii lähevad kartulid maksma 0,7xeurot, oad 1,4y eurot ning mõlemad kokku 0,7x + 1,4y eurot. Tahaksime seda maksumust minimeerida, kusjuures kogustele x ning y on seatud teatud piirangud, mis tulevad päevastest toitainete normidest – peame sööma vähemalt teatud arvu valke ja süsivesikuid.
Üritame nüüd need piirangud võrratuste keeles kirja panna.
Valke on kartulites 20x grammi ja ubades 60ygrammi. Kuna täiskasvanud inimene peaks päevas sööma vähemalt 50 grammi valke, siis saame võrratuse 20x + 60y ≥ 50.
Sarnaselt saame süsivesikute jaoks tingimuse 170x + 120y ≥ 300.
Lisaks ei saa ei kartulite ega ubade kogused olla negatiivsed arvud. Seetõttu on meil veel võrratused x≥ 0 ja y ≥ 0
Oleme saanud järgneva matemaatilise mudeli. „min” tähendab siin, et otsime võrrandi väikseimat ehk minimaalset väärtust ning muidugi peavad lisaks olema rahuldatud kõik toodud võrratused:
Seda ülesannet on kõige lihtsam lahendada graafiliselt. Selleks kanname koordinaatteljestikku kõik neli võrratust ning märgime ära piirkonna, mis kõiki võrratusi rahuldab.
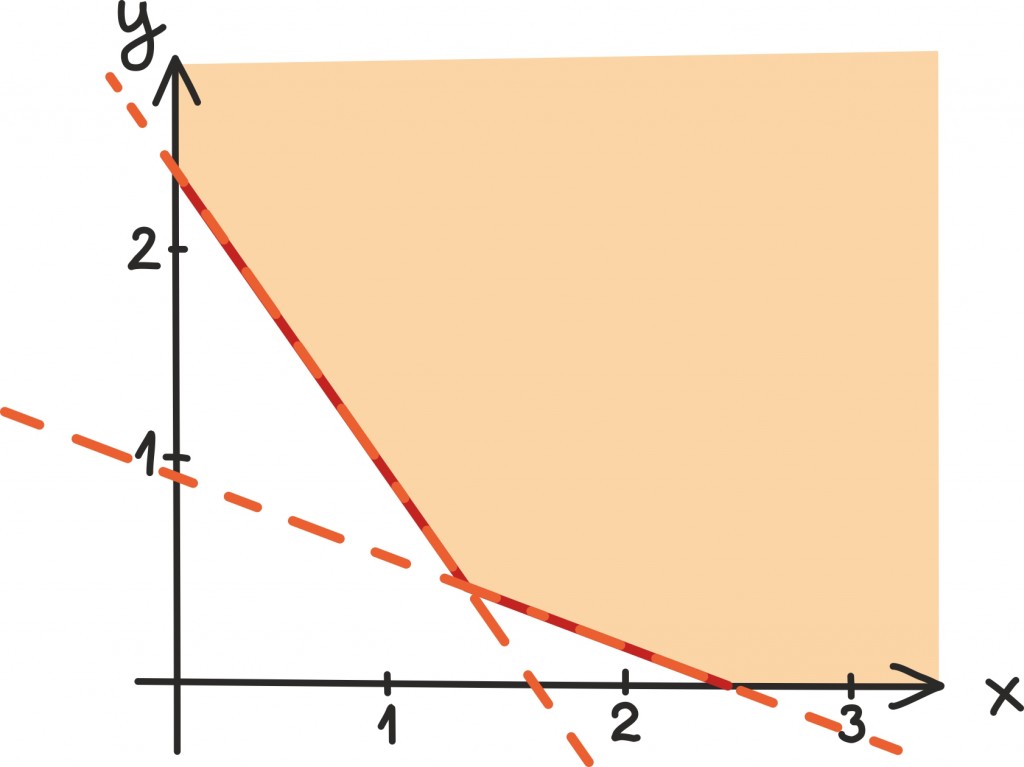
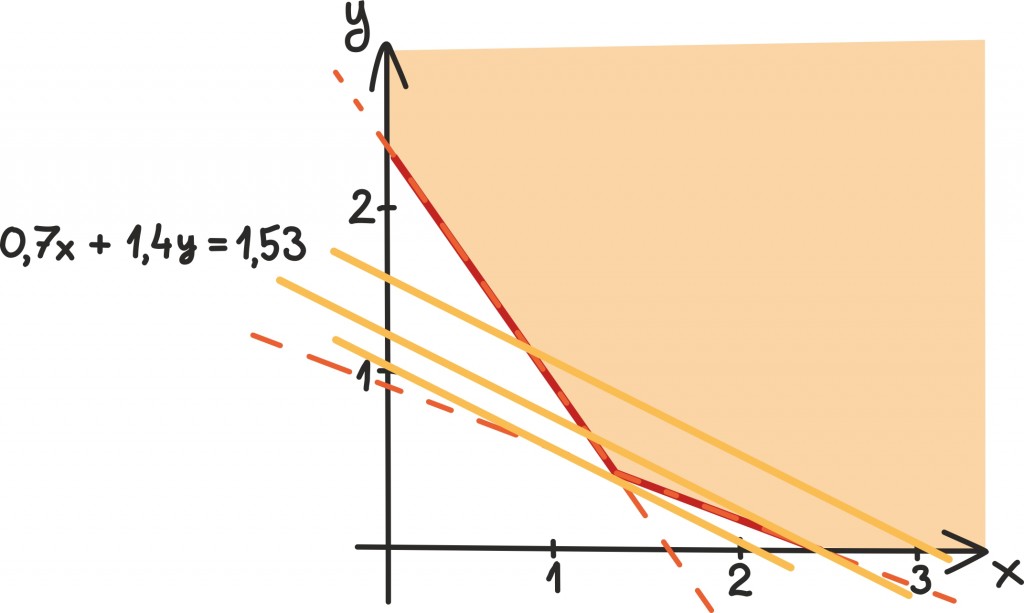
Viimaks leiame märgistatud piirkonnas punkti, kus funktsiooni 0,7x + 1,4y väärtus on minimaalne. Kuidas seda teha?
Meenutame, et sirged kujus 0,7x + 1,4y = c on kõik omavahel paralleelsed ning vähendades c väärtust, liigutame seda sirget lihtsalt allapoole. Nüüd asub 0,7x + 1,4y minimaalne väärtus kindlasti ühel sellistest sirgetest ning lahendiks on paar (x, y) täpselt siis, kui ta ka omakorda lahendipiirkonda jääb. Seega on meie ülesanne leida minimaalne c väärtus, mille korral sirge 0,7x + 1,4y = c lõikab veel endiselt lahendipiirkonda.
Nagu jooniselt näeme, juhtub see täpselt sirgete 20x+ 60y = 50 ja 170x + 120y = 130 lõikumispunktis, mida oskame juba lihtsalt leida: 1,54 kg kartuleid ja 0,32 kg ubasid lähevad maksma 1,53 eurot.
Mõned levinud võrratused
Nii nagu koolist on hästi teada, et õpetaja on alati targem kui õpilane, kehtivad ka teatud võrratused väga paljude erinevate arvude või elementide jaoks. Näiteks kehtivad mõned võrratused absoluutselt kõikide positiivsete reaalarvude jaoks või kõikide ühest suuremate reaalarvude jaoks või kõikvõimalike kolmnurkade jaoks. Loetleme ja selgitame neist siinkohal mõnda.
Reaalarvu ruut
Kõige tuntum võrratus on ilmselt järgmine: iga reaalarvu ruut on mittenegatiivne ehk a2 ≥ 0. Võrdus kehtib muidugi parajasti juhul, kui a on võrdne nulliga. Miks see ikkagi on nii?
Nulli puhul on muidugi asi selge, on ju nulli ruut jällegi null.
Ka positiivsete arvude puhul pole asi palju keerulisem: a2 on ju täpselt küljega a ruudu pindala ning ruudu pindala peabki positiivne olema.
Iga negatiivse arvu võime aga kirjutada kujul –a = (–1) · a, kus a on ise positiivne. Sel juhul võime kirjutada
ning tulemus on jällegi positiivne.
Kumb on suurem, arv või tema ruut?
Võibolla kõlab see alguses natuke mitteintuitiivselt, aga arvu ruut ei ole mitte sugugi alati suurem kui arv ise. Negatiivse arvu ruut on muidugi alati temast suurem, sest eelneva põhjal on arvuruut ise alati positiivne.
Samuti, kui positiivne reaalarv on ühest suurem, siis on ta ruut arvust suurem. Kui aga positiivne reaalarv on ühest väiksem, siis on ta ruut arvust väiksem:
Ka seda pole väga raske tõestada – teame ju, et võime iga võrratust positiivse täisarvuga läbi korrutada:
- korrutades võrratuses a >1 mõlemad pooled a-ga, saame võrratuse a2 > a,
- korrutades võrratuses a < 1 mõlemad pooled a-ga, saame võrratuse a2 < a.
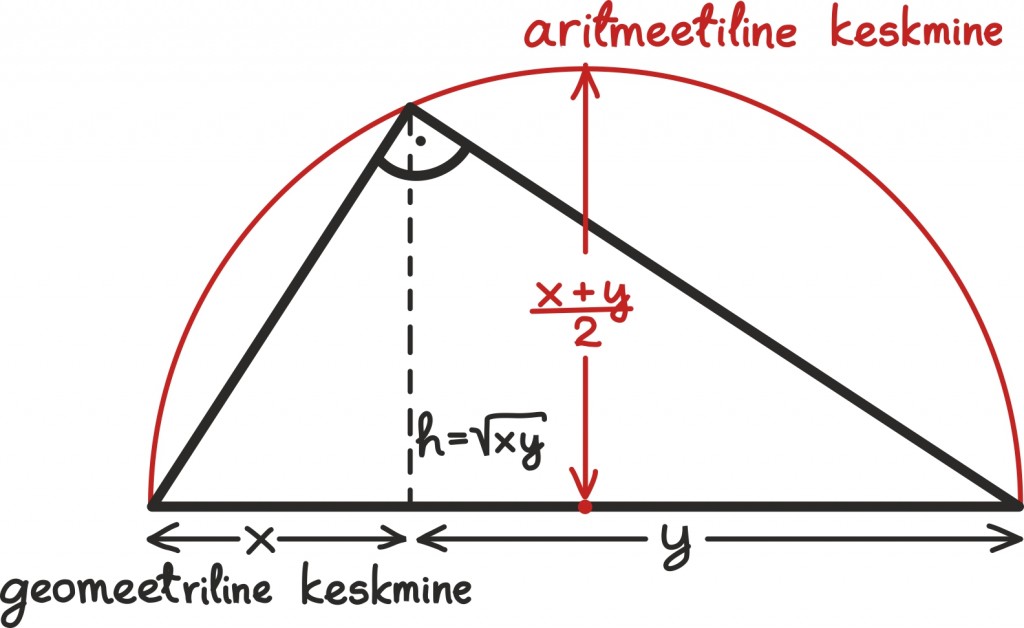
Aritmeetiline ja geomeetriline keskmine
Arvude aritmeetiline keskmine tuleb esile üsna tihti: näiteks arvutatakse välja keskmist hinnet, eksamitulemuste keskmist või rahva keskmist vanust. Selle jaoks liidetakse lihtsalt kõik uuritavad tulemused kokku ja jagatakse summa tulemuste arvuga:
Keskmistada võib aga teisiti: võib kõik tulemused kokku korrutada ning siis võtta nendest nii mitmes juur, kui palju tulemusi oli.
Geomeetriline keskmine tuleb esile näiteks televiisorite kuvasuhete määramises. Vana kinostandard oli kuvasuhe 2,39:1 (pilt on 2,39 korda laiem) ning vana televiisor näitas filme suhtes 4:3. Nende kahe standardi vahel kompromissi leidmiseks kasutati geomeetrilist keskmist ning saadi tulemuseks 16:9 standard. Geomeetrilise keskmise kasutamine võimaldas saavutada olukorra, kus mõlemaid proportsioone „muudeti” ühepalju.
Nii aritmeetiline kui geomeetriline keskmine on ka seotud vastavanimeliste jadadega [lk 128]. Nimelt on aritmeetilise jada kolmest järjestikusest liikmest keskmine äärmiste aritmeetiliseks keskmiseks ning täpselt sama juhtub ka geomeetrilises jadas, kasutades geomeetrilist keskmist.
Üks tuntud võrratus väidab, et kahe mittenegatiivse reaalarvu aritmeetiline keskmine on vähemalt sama suur kui kahe arvu geomeetriline keskmine. Ehk:
Kuidas seda tõestada?
Vaatame arvu
Kuna tegemist on arvuruuduga, siis on ta mittenegatiivne. Avades sulud, saame
ehk tõesti
Graafiliselt võib aritmeetilisest ja geomeetrilisest keskmisest ning nendevahelisest võrratusest mõelda järgnevalt:
Tõestus vajaks natuke kolmnurkade ja trigonomeetriaga mängimist. Huvitunud lugeja võib seda proovida näiteks peale trigonomeetria peatüki läbimist [lk 205].
Kuigi meie tõestasime siin ainult, et kahe arvu aritmeetiline keskmine on suurem geomeetrilisest keskmisest, siis tegelikult kehtib väide mistahes paljude arvude kohta. Suvalise mittenegatiivse arvu aritmeetiline keskmine on suurem kui geomeetriline keskmine. Seda on siiski juba pisut keerulisem tõestada.
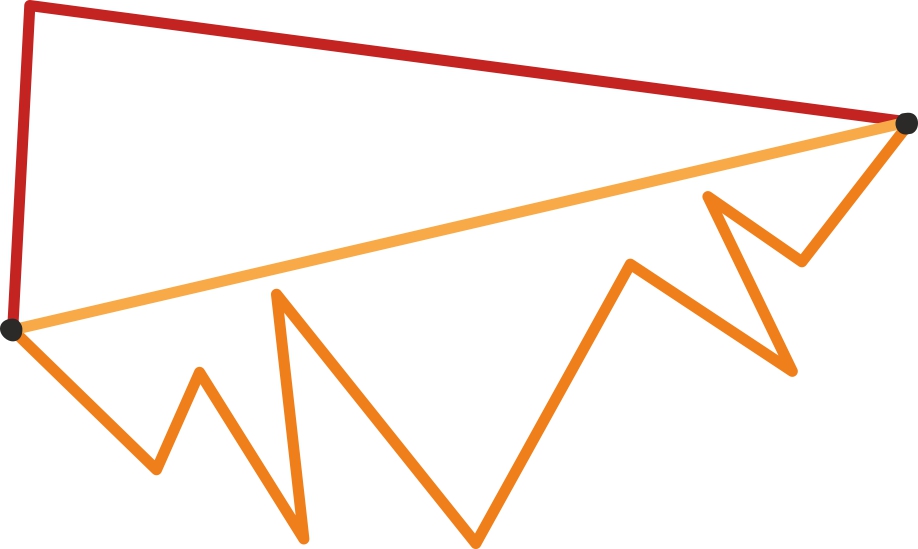
Lühim murdjoon
Lõpetame peatüki ühe väga lihtsa geomeetrilise võrratusega. See väidab, et kahe punkti vahelistest murdjoontest on vähima pikkusega neid punkte ühendav sirglõik.
Sellest võrratusest järeldub kohe näiteks tuntud kolmnurga võrratus: kolmnurga iga kahe küljepikkuse summa on pikem kui kolmas külg. See lihtne väide osutub järelikult üsna sisukaks.