KIIRUSE GRAAFIK JA LÄBITUD TEEPIKKUS/NIHE

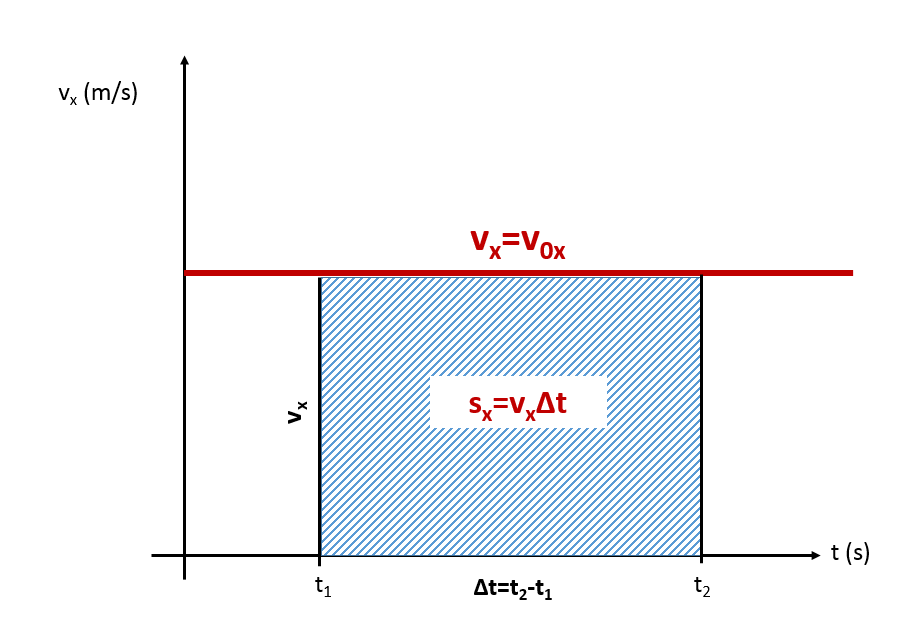
Liikugu keha ajavahemikul Δt=t₂-t₁ ühtlase kiirusega v_0x. Sellise liikumise korral on keha kiiruse võrrand, v_x=v_0x, sest ühtlasel liikumisel a_x=0 ja v_x=v_0x ning selle kiiruse graafikuks on ajateljega horisontaalne sirge.

Markeerime abijoontega vaatluse alg- ja lõpphetked ning märkame, et graafiku alla abijoonte vahele jäävaks kujundiks on ristkülik. Arvutame selle kujundi pindala.

Sulle võivad huvi pakkuda need õppematerjalid:

Ristküliku pindala avaldub teatavasti külgede pikkuste korrutisega. Meie ristküliku ühe külje pikkus on võrdne keha kiirusega (v_x) ja teise külje pikkus ajavahemikuga (Δt). Seega:

Sx=v_x∙Δt.

Märkame, et kiiruse ja ajavahemiku korrutis on võrdne keha poolt läbitud teepikkusega (sooritatud nihkega).

Taolist, kiiruse (või muu suuruse) graafiku alla jääva kujundi pindala kaudu teepikkuse (või muu suuruse) leidmist nimetatakse graafilise integreerimise meetodiks.

See artikkel on retsenseerimata.
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!

Õpikud

Vaata kõiki õpikuid

KIIRUSE GRAAFIK JA LÄBITUD TEEPIKKUS/NIHE

Sulle võivad huvi pakkuda need õppematerjalid:

Tundetarkus lastele. VASTIKUS

Funktsioonide graafikute lõikepunktide leidmine

Õpime tähti. L-täht

Kirjalik lahutamine

Harjuta eesti keelt A2-B1. Lugemine

MEISTERDA! Papist kevadlill

MEISTERDA! Looma näoga kaart jõuludeks

Peastarvutamine I kooliastmele

Funktsioonide graafikud

Õpime tähti. M-täht

I ja J-i õigekiri

Protsendid põhikooli matemaatikas

Eesti keele grammatika kordamine 9. klassile

Liitmine 20 piires

Õpime tähti. T-täht

Ioonid

Õpikud