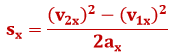Nihe ühtlaselt muutuval sirgjoonelisel liikumisel
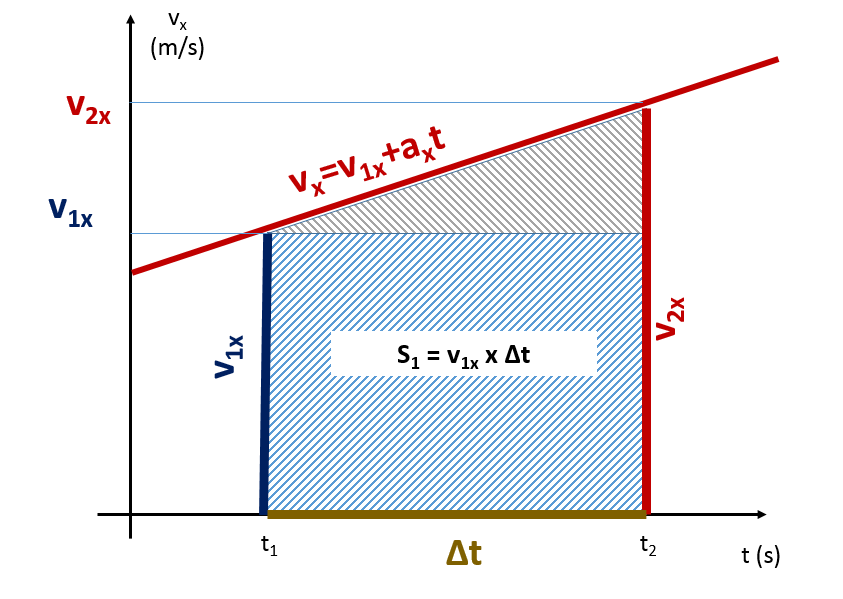
Leiame graafilise integreerimise meetodi abil valemi nihke leidmiseks ühtlaselt muutuval sirgjoonelisel liikumisel. Kiiruse võrrand ühtlaselt muutuval sirgjoonelisel liikumisel on:
Vaatleme olukorda, kus keha liigub kiirenevalt st v0x>0 ja ax>0. Rõhutagem siinjuures, et samale tulemusele jõuaksime ka aeglustuva liikumise korral. Kirjeldatud juhtumil on kiiruse graafikuks tõusev sirge.
Sulle võivad huvi pakkuda need õppematerjalid:
Eesti keele grammatika kordamine 9. klassile
Protsendid põhikooli matemaatikas
Liitmine 20 piires
Põhiseadus selgeks! Kordamine põhikooli ühiskonnaõpetuse lõpueksamiks
Harjutamine teeb meistriks: eesti keele käänded
Õpime tähti. G-täht
Väike funktsiooniamps
Numbrilised seosed
Eesti keele grammatika gümnaasiumile: numbrite kirjutamine
Õpime tähti. L-täht
Õpime tähti. Š-täht
Tundetarkus lastele. ÜLLATUS
Allar Veelmaa videotund. Avaldised
Seega kiireneva liikumise korral tekib ajavahemiku Δt = t2 – t1 korral kiiruse graafiku alla trapets, mille alusteks on vastavalt kiirused ajahetkedel t1 (v1x,algkiirus) ja t2 (v2x,lõppkiirus) ning kõrguseks ajavahemik ∆t.
Trapetsi pindala (meie juhtumil läbitud teepikkus, sooritatud nihe) leitakse aluste pikkuste summa ja kõrguse poole korrutisena:
Laskumata pikemalt valemite tuletamise üksikasjadesse saab näidata, et
või
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!
