A-tüüpi mõõtemääramatuse (juhusliku määramatuse) leidmine. Standardhälve
A-tüüpi mõõtemääramatuse arvutamisel kasutatakse matemaatilise statistika valemeid.
(1) Kui sooritatakse kindel arv n mõõtmisi, mõõteväärtustega x1, x2, x3 … xn, siis väljendab mõõtmistulemuste aritmeetiline keskmine ehk tõenäoliseim väärtus, väärtust mis vastab kõige paremini mõõdetava suuruse tegelikule väärtusele:
Sulle võivad huvi pakkuda need õppematerjalid:
Jane Snaith. Traumateadlik kool
Õpime tähti. N-täht
KEISRI UUED RÕIVAD. Muinasjutt kuulamiseks
Algebralised murrud
Urme Raadik ja Sille Jõgeva. Omavahelised suhted
Kirjeldav statistika
Õpime tähti. A-täht
Eesti keele grammatika gümnaasiumile: numbrite kirjutamine
Eesti keele grammatika kordamine 7. klassile
Numbrilised seosed
Üksliikmed, hulkliikmed ja tehted nendega
Väike funktsiooniamps
Ruutvõrrandi abil lahenduvad tekstülesanded
(2) Mõõtmiste hajuvust iseloomustatakse dispersiooniga:
(3) Mõõtemääramatus on seotud standardhälbega:
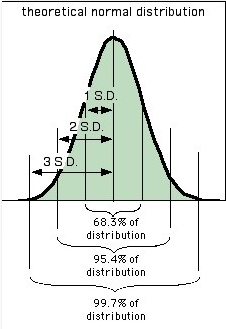
Standardhälve iseloomustab üksikute mõõteväärtuste juhuslikku hajuvust suuruse keskväärtuse ümber. Kasutades mõõtemääramatusena standardhälbega võrdset väärtust Δx=σ, saame mõõtmiste normaaljaotusele vastavuse korral usaldusnivooks 68%, mis tähendab, et keskmiselt igal kahel mõõtmisel kolmest esinev mõõteviga on mõõtemääramatusest väiksem või sellega võrdne.
Kui soovime usaldatavust suurendada, tuleb standardhälvet korrutada katteteguriga, mis omakorda sõltub mõõdiste jaotusest ning nõutavast usaldusnivoost. Kui soovime, et mõõtmiste usaldusnivoo oleks 95%, tuleb standardhälvet korrutada kahega (Δx=2σ), kui aga enam kui 99% usaldatavust, siis kolmega (Δx=3σ).
Kui mõõtmisel esineb (ja enamasti esinebki) nii A- (ΔxA) kui B-tüüpi (ΔxB) mõõtemääramatusi, leitakse kogumääramatus (Δx) valemist:
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!
