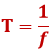Kiirus ühtlasel ringjoonelisel liikumisel

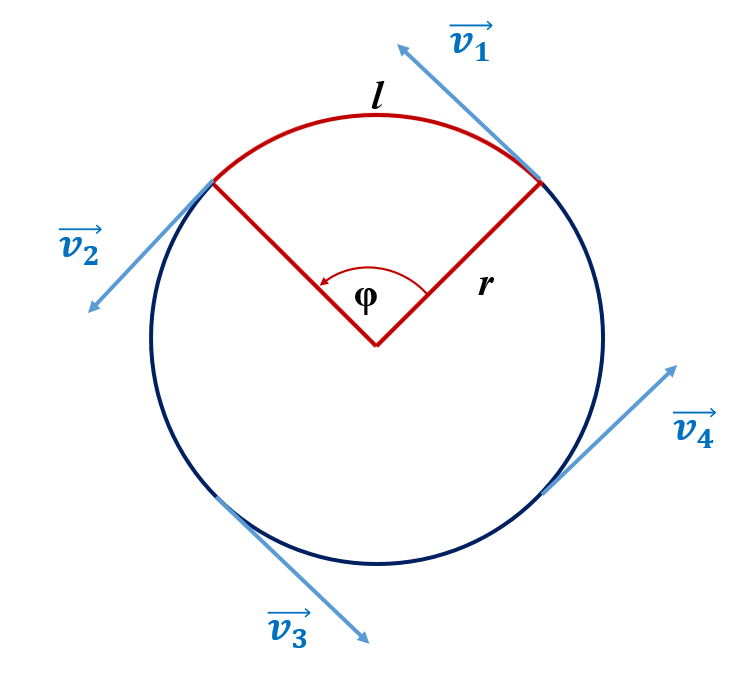
Ühtlaseks ringjooneliseks liikumiseks nimetatakse lii­ku­mist, kus keha liigub ringjoonelisel trajek­too­ril ning tema kiiruse mooduli väärtus (joonkiirus) ajas ei muu­tu.

v₁ = v₂ = v₃ = v₄ = …

Tuleb rõhutada, et ringjooneliselt liikuva keha kiirus kui vektor muutub pidevalt, sest muutub kiirusvek­tori suund.

Ringjoonelise liikumise kirjeldamiseks kasutatakse pöör­denurka φ – so kesknurk, mis jääb raadiuse algse ning pöördunud asendi vahele.

Pöördenurka mõõdetakse radiaanides. 1 radiaan on selline kesknurk, mille korral nurga haarade vahele jääva kaare pikkus on võrdne ringjoone raadiusega.

Nurkkiirus on füüsikaline suurus, mis iseloomustab keha trajektoori raadiuse poolt ajavahemikus Δt kae­tavat pöör­de­nurka φ:

Nurkkiirust mõõdetakse radiaanides sekundis: 1 rad/s

(Muutumatut) kiirust, millega keha liigub mööda ringjoone kaart nimetatakse keha joonkiiruseks (v). Keha poolt läbitud kaare (tee)pikkus l on võrdeline trajektoori raadiuse r ja pöördenurgaga φ:

Joonkiirus v on seega samuti võrdeline trajektoori raadiusega r ja nurkkiirusega :

Ajavahemikku, mille jooksul läbib keha ühe täisringi (teeb täispöörde), nimetatakse pöörlemis­perioodiks (T).

Füüsikalist suurust, mis iseloomustab täispöörete arvu ajaühikus nimetatakse keha pöörlemis­sa­ge­duseks .

Ühe täispoorde korral kaetakse pöördenurk φ = 360° = π rad. Nii saame avaldada nurkkiiruse  pöör­lemis­sageduse f ja/või –perioodi T kaudu: