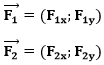Kui keha on samaaegselt vastastikmõjus mitme kehaga, siis võrdub tema liikumise kiirendus nende kehade poolt põhjustatud kiirenduste, millega keha liiguks teiste kehade mõjude puudumisel, vektorsummaga – seega kui kehale mõjub samaaegselt mitu jõudu, tuleb need jõud liita omavahel nagu vektorid.

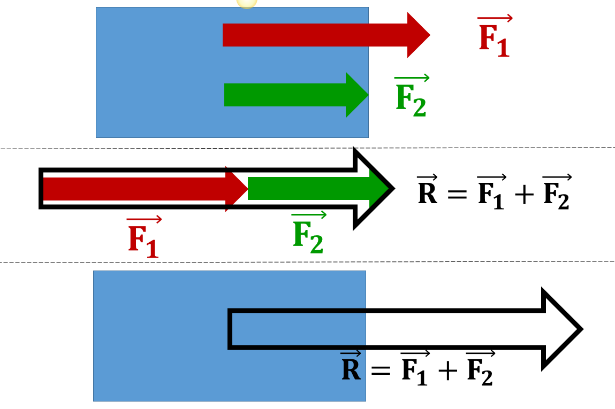
Kehale mõjuvate jõudude vektorsummat nimetatakse nende jõudude resultandiks ehk resul­tantjõuks.

Kui kehale mõjuvad jõud on samasuunalised, siis nende mõjud liituvad – resultantjõu moodul on võrdne komponentide moodulite summaga.

Kuna liidetavad vektorid on samasuunalised, siis on loomulikult ka resultantjõu suund sama.

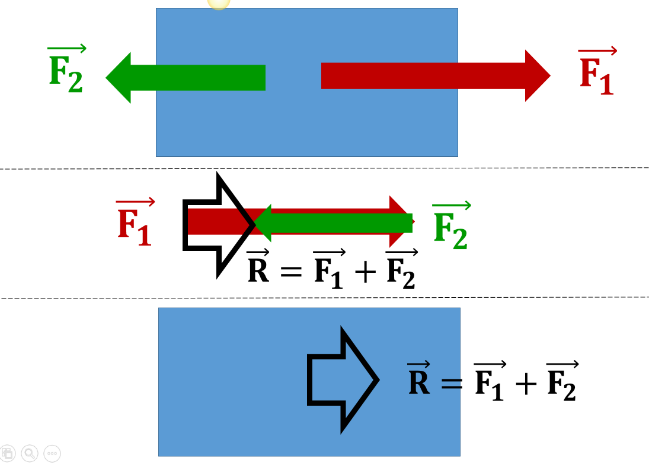
Kui kehale mõjuvad jõud on vastassuunalised, siis nende mõjud nõrgendavad teineteist – resultantjõu moodul on võrdne komponentide moodulite vahega.

Kui resultantjõu mooduli väärtus on negatiivne, tuleb seda tõlgendada kui asjaolu, et resultantjõu suund langeb kokku teise liidetava suunaga , kui positiivne, on resultantjõu suund sama kui esimesel liidetaval .

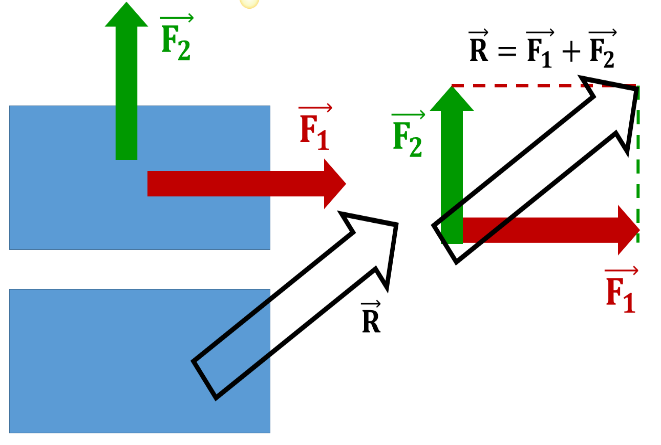
Kui kehale mõjuvad jõud on teineteisega risti, saab resultantjõu mooduli leidmiseks kasutada Phyta­go­ra­se seadust:

Risti asetsevate jõudude resultantjõu suuna saame mää­rata tangensi (vastas­kaatet jagatud lähiskaa­te­ti­ga) pöördfunktsiooni abil.

kus α on nurk resultantvektori ning esimese liidetava vahel .

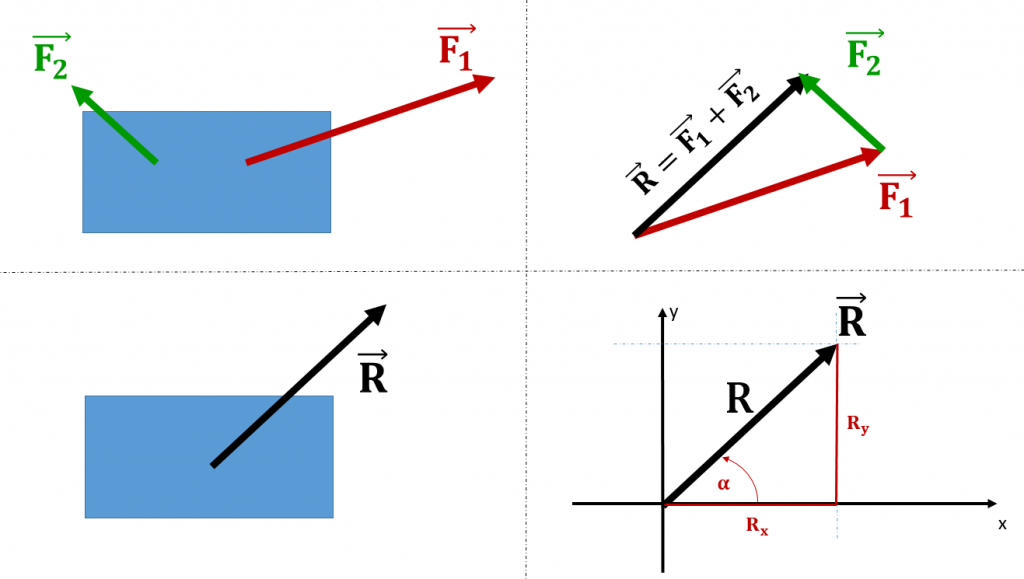
Kui liituvad jõud asuvad suvalise nurga all, tuleb nende liitmiseks lahutada jõud komponentideks ning liita omavahel vastavad komponendid:

ning need omakorda avalduvad jõudude moodulite ning x-telje positiivse suuna vaheliste nurkade kaudu

F_1x=F₁cosα₁         F_1y=F₁sinα₁ F_2x=F₂cosα₂         F_2y=F₂sinα₂

Kui

ning

ja

R_x=F_1x+ F_2x=F₁cosα₁+ F₂cosα₂

R_y=F_1y+ F_2y=F₁sinα₁+ F₂sinα₂

Resultantjõu suuna leiame jälle tangensi pöördfunktsioonina:

ning α on nurk resultantvektori ning x-telje positiivse suuna vahel.

NB! Kalkulaatoriga arvutamisel tuleb jälgida asjaolu, et kui kalkulaator väljastab tangensi pöördfunktsiooni väärtuseks x° siis α leidmiseks

1) kui R_y>0 ja R_x>0 => siis 0° <α< 90°  ehk α = x;

2) kui R_y>0 ja R_x<0 => siis 90° <α< 180° ehk α = 180°+x;

3) kui R_y<0 ja R_x<0 => siis 180° <α< 270° ehk α = 180°+x;

4) kui R_y<0 ja R_x>0 => siis 270° <α< 360°ehk α = 360°+x