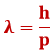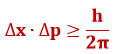Kvantmehaanika
Osakeste leiulained
Bohr’i aatomi planetaarmudel võimaldas küll selgitada miks aatomid ei kiirga elektromagnetlaineid või kui suur on ühel või teisel orbiidil elektroni energia, kuid ta ei anna vastust küsimusele miks just need orbiidid on lubatud ja teised mitte.
1924. aastal esitles prantsuse füüsik Louis de Broglie käsitlusviisi, mille kohaselt saab kõigi aineliste liikuvate objektidega siduda teatavat liiki laine – leiulaine (ka tõenäosuslaine, mateerialaine), mille lainepikkus on pöördvõrdeline selle keha liikumishulgaga:
Sulle võivad huvi pakkuda need õppematerjalid:
Знакомство с химией
Õpime tähti. D-täht
Eesti keele grammatika gümnaasiumile: numbrite kirjutamine
Tundetarkus lastele. PÕHIEMOTSIOONID
Растворы
II kooliastme matemaatika reeglite kordamine
Funktsioonide graafikud
Tundetarkus lastele. RÕÕM
VAPPER TINASÕDUR. Muinasjutt kuulamiseks
Õpime värve!
Ruutvõrrand
Õpime tähti. G-täht
Õpime tähti. L-täht
8. klassi matemaatika teooriavideod
Harjutamine teeb meistriks: kuhu käib koma?
Minni Aia-Utsal. Tõhusad enesekohased ja sotsiaalsed oskused
kus λ – mateerialaine lainepikkus, h = 6,62∙10-34Js – Plancki konstant ja p =mv – keha liikumishulk (kus m – keha mass, v – keha kiirus)
Seega laienes valguse korpuskulaar-laineline dualism kõikidele liikuvatele objektidele.
Miks ei me märka igapäeva elus meist mööduvaid kehi „lainetamas“?
Pole keeruline välja arvutada, et 70kg massiga inimese, kes liigub jalakäija kiirusega (6 km/h ≈ 1,7 m/s) leiulaine lainepikkus on umbes 5,6∙10-36m. Siinkohal on paslik meenutada, et inimkonna sisemine nähtavushorisont jääb käesoleval ajal suurusjärku 10-21m – seega on inimese leiulaine lainepikkus 1015 väiksem kui füüsikute käsutuses olevad seadmed mõõta võimaldavad.
Elektronide difraktsioon
Milline on leiulaine lainepikkus aga juhul, kui liikuvaks kehaks on elektron, mille mass on 9,1×10-31kg ning mis liigub kiirusega 10 000 km/s (energia umbes 300 eV)?
Arvutused näitavad, et sellise elektroni leiulaine pikkus on umbes 70pm. Võrdluseks olgu meelde tuletatud, et nähtava valguse lainepikkus jäi vahemikku 380 … 760pm – ehk tegu on ultravioletsesse piirkonda jäävale elektromagnetlainele vastava lainepikkusega, mis on kaasaja vahenditega täiesti mõõdetav.
1927. aastal avastatigi elektrone, mis on ainelise mateeria ühed väiksemad koostisosakesed – st neil on kõik osakesele iseloomulikud omadused: mass, kuju, ruumala, läbi kitsaste pilude juhtides, et elektronid käituvad läbi mitme kitsa pilu minekul lainena.
Seda nähtust nimetatakse elektronide difraktsiooniks.
Kui elektronide teele asetada vaid üksik kitsas pilu, samuti enamikus teistes olukordades, käituvad nad aga kui osakesed.
Määramatusseos
Analüüsides de Broglie’ korpuskulaar-lainelist dualismi, jõudis saksa füüsik Werner Heisenberg 1927. aastal järeldusele, et ühegi liikuva keha asukohta ja liikumishulka (sisuliselt kiirust) ei ole võimalik samaaegselt määrata kuitahes täpselt, vaid nende samaaegsel mõõtmisel kehtib määramatus:
kus ∆x – keha asukoha määramatus; ∆p=m∆v+v∆m – keha liikumishulga määramatus (m – keha mass, Δm – massi määramatus, v – keha kiirus, Δv – kiiruse määramatus), h = 6,62∙10-34Js – Plancki konstant.
Kirjeldatud põhimõte pole kooskõlas meie igapäevase kogemusega – mõõdavad ju politseinikud autode kiirust ja asukohta samaaegselt ning teevad kiiruse ületajatele protokolle?
Leiame auto massiga 1000±1 kg (suhteline määramatus 0,1%) ning liigub kiirusega 100±1 km/h (suhteline määramatus 1%) asukoha määramatuse. Auto liikumishulgaks saame ligikaudu 28 000±300 kgms-1 (suhteline määramatus 1,1%) – seega asukoha määramatus:
mis on taas palju-palju väiksem kui inimkonna sisemine nähtavushorisont.
Kui aga liikuvaks objektiks oleks elektron, mille mõõtmeteks hinnatakse umbes 10-18m ning mille mass on 9,1×10-31kg ja liigub kiirusega 10 000 km/s (energia umbes 300 eV)? Eeldame, et elektroni kiiruse ja massi mõõtmisel on suhteline mõõtemääramatus autoga samas suurusjärgus. Seega tuleb elektroni liikumishulga määramatus 2,8∙10-26kgms-1 ning asukoha määramatus:
Määramatus tundub olevat samuti tühine?
Tõdeme siiski, et elektroni asukoha määrmatus on umbes 109 korda elektroni mõõtmetest suurem! Kui teisendame selle määramatuse autoga (mõõtmed 5m) võrreldavatesse mastaapidesse, saaksime elektroni (mis on kasvanud autoga samasse mõõtu) asukoha mõõtemääramatuseks umbes 5∙109m = 5 000 000 km ehk ringjoon, mis tähistaks (auto mõõtu) elektroni asukohta ulatuks umbes 13 korda nii kaugele kui asub Maast Kuu.
Püüa siis sellisele täpsusega asukohaga mõõdetud autole teha trahvi kiiruse ületamise eest 🙂
Schrödingeri võrrand. Kvantmehaanika
Üldistades de Broglie leiulainest ning Heisenbergi määramatusseosest tulenevaid järeldusi üldistas Saksa füüsik Erwin Schrödinger võrrandiks nn Schrödingeri võrrandiks, mis on analoogiks klassikalisest mehaanikast tuttavale liikumisvõrrandile ning kirjeldab mikromaailma objektide – aatomite, molekulide, aga ka nendes sisalduvate prootonite, neutronite ja elektronide liikumisolekuid.
Schrödingeri võrrandi peamine erinevus meile tuttavast liikumisvõrrandist on see, et tema lahendiks pole mitte osakese asukoht või kiirus või kiirendus mingil ajahetkel vaid hoopis osakese leiulaine suvalisel ajahetkel.
Füüsika haru, mis kasutab osakeste asukoha ja liikumise kirjeldamisel Schrödingeri võrrandit nimetatakse kvantmehaanikaks.
Olgu siinkohal lihtsalt ettekujutuse saamiseks toodud Schrödingeri võrrandi üldkuju:
kus u ongi otsitav lainefunktsioon.
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!