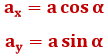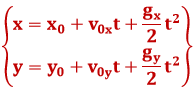Erisihiliste liikumiste sõltumatus

Kuna kiirus ja kiirendus on mõlemad vektorid, siis on võimalik nad (samuti neid sisaldavad avaldised) jagada mooduliteks (komponentideks, koordinaatideks), kasutades selleks põhikooli mate­maa­ti­kakursusest tuttavaid siinus- või koosinusteoreeme.

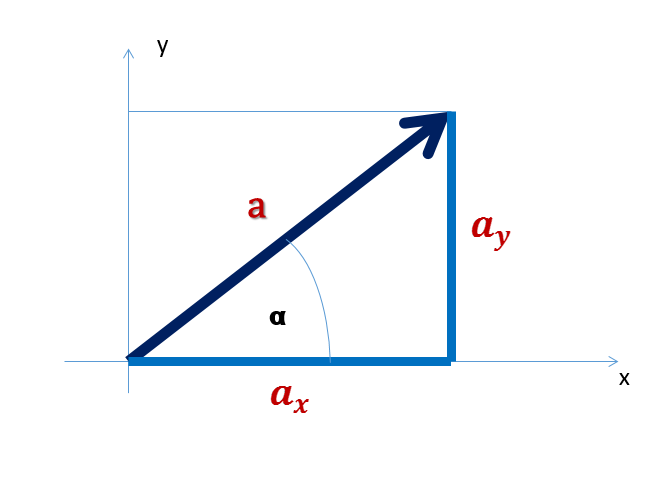
Kui mõõdame nurka abstisstelje (horisontaalne telg) po­si­tiivsest suunast vektorini, tehes seda kellaosutile vastassuunas, saab mistahes vektori x- ja y-koordinaadid  avaldada järgmiselt:

NB! Kui nurka mõõdetakse teisiti (kellaosuti suunas, y-teljest, x-telje negatiivsest suunast vms), tuleb jälgida põhimõtet, et siinus on vastaskaateti ja hüpotenuusi ning koosinus lähiskaateti ja hüpotenuusi jagatis.

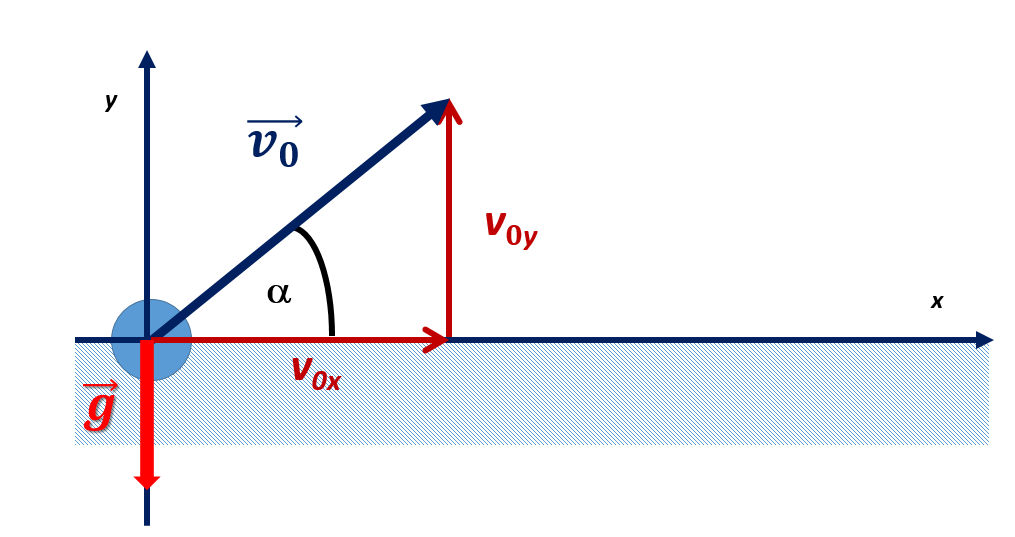
Vaatleme näiteks Maapinnalt horisondiga nurga α all kiirusega v₀ kaldu visatud keha liikumist eeldusel, et kehale ei mõju õhutakistus (ainuke kehale mõjuv jõud on Maa raskusjõud st keha liigub vaba langemise kiirendusega g≈9,81 m/s²).

Taolise keha liikumisvõrrand (vektorkujul) on:

kus  – keha asukohavektor (asukoht suvalisel ajahetkel);  – keha algasukoha vektor (algasukoht);  – keha algkiirus,  – keha kiirendus (vaba langemise kiirendus) ning t – vaatlushetk.

Keha kiiruse võrrand (vektorvõrrand) aga

kus – keha kiirusvektor (kiirus suvalisel ajahetkel); – keha algkiirus, – keha kiirendus (vaba langemise kiirendus) ning t – vaatlushetk.

Lahutame liikumis- ja kiirusevõrrandid komponentideks (mooduliteks, koordinaatideks):

Leiame komponentide väärtused.

Algasukoht: x₀=0; y₀=0

Algkiirus: v_0x=v₀cosα; v_0y= v₀sinα

(Vaba langemise) kiirendus: g_x=gcos270°; g_y=gsin270°. NB! cos270°=0; sin270°=-1 à g_x=0; g_y=-g

Nii saame kiiruse koordinaatvõrranditeks:

ning liikumisvõrranditeks:

Võrranditest nähtub, et horisontaalsihis liigub taoline keha ühtlaselt, vertikaalsihis aga ühtlaselt muutuva kiirusega.