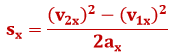Nihe ühtlaselt muutuval sirgjoonelisel liikumisel

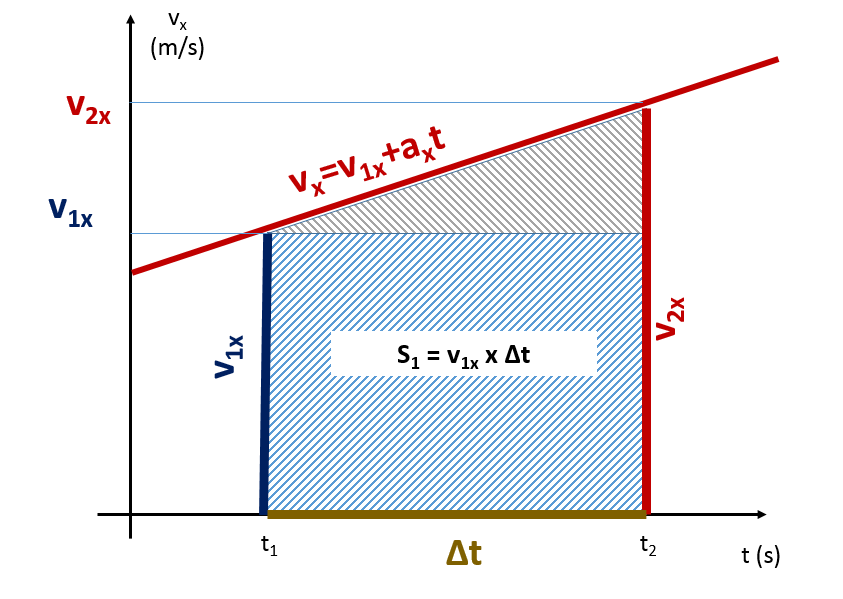
Leiame graafilise integreerimise meetodi abil valemi nihke leidmiseks ühtlaselt muutuval sirgjoonelisel liikumisel. Kiiruse võrrand ühtlaselt muutuval sirgjoonelisel liikumisel on:

Vaatleme olukorda, kus keha liigub kiirenevalt st v_0x>0 ja a_x>0. Rõhutagem siinjuures, et samale tulemusele jõuaksime ka aeglustuva liikumise korral. Kirjeldatud juhtumil on kiiruse graafikuks tõusev sirge.

Sulle võivad huvi pakkuda need õppematerjalid:

Seega kiireneva liikumise korral tekib ajavahemiku Δt = t₂ – t₁ korral kiiruse graafiku alla trapets, mille alusteks on vastavalt kiirused ajahetkedel t₁ (v_1x,algkiirus) ja t₂(v_2x,lõppkiirus) ning kõrguseks ajavahemik ∆t.

Trapetsi pindala (meie juhtumil läbitud teepikkus, sooritatud nihe) leitakse aluste pikkuste summa ja kõrguse poole korrutisena:

Laskumata pikemalt valemite tuletamise üksikasjadesse saab näidata, et

või

See artikkel on retsenseerimata.
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!

Õpikud

Vaata kõiki õpikuid

Nihe ühtlaselt muutuval sirgjoonelisel liikumisel

Sulle võivad huvi pakkuda need õppematerjalid:

Kuidas ja miks saada Ameerika presidendiks?

Oksüdatsiooniaste

Õpime tähti. Ö-täht

Õpime tähti. N-täht

Lahutamine 20 piires

Tundetarkus lastele. PÕHIEMOTSIOONID

Õpi eesti keelt teise keelena B2. Grammatika

Urme Raadik ja Sille Jõgeva. Omavahelised suhted

KEISRI UUED RÕIVAD. Muinasjutt kuulamiseks

Ruutvõrrandi abil lahenduvad tekstülesanded

Peastarvutamine eelkoolile

Eesti keele grammatika kordamine 4. klassile

Õpime tähti. Ä-täht.

Õpime tähti. D-täht

Õpikud