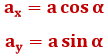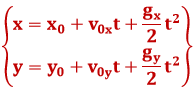Kuna kiirus ja kiirendus on mõlemad vektorid, siis on võimalik nad (samuti neid sisaldavad avaldised) jagada mooduliteks (komponentideks, koordinaatideks), kasutades selleks põhikooli matemaatikakursusest tuttavaid siinus- või koosinusteoreeme.
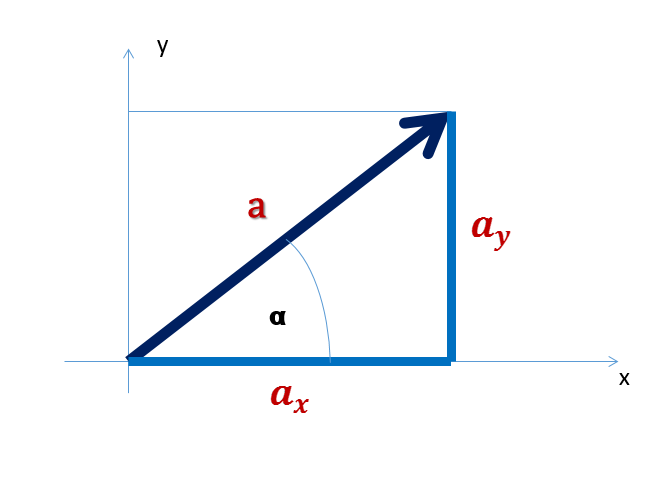
Kui mõõdame nurka abstisstelje (horisontaalne telg) positiivsest suunast vektorini, tehes seda kellaosutile vastassuunas, saab mistahes vektori x- ja y-koordinaadid 
avaldada järgmiselt:
NB! Kui nurka mõõdetakse teisiti (kellaosuti suunas, y-teljest, x-telje negatiivsest suunast vms), tuleb jälgida põhimõtet, et siinus on vastaskaateti ja hüpotenuusi ning koosinus lähiskaateti ja hüpotenuusi jagatis.
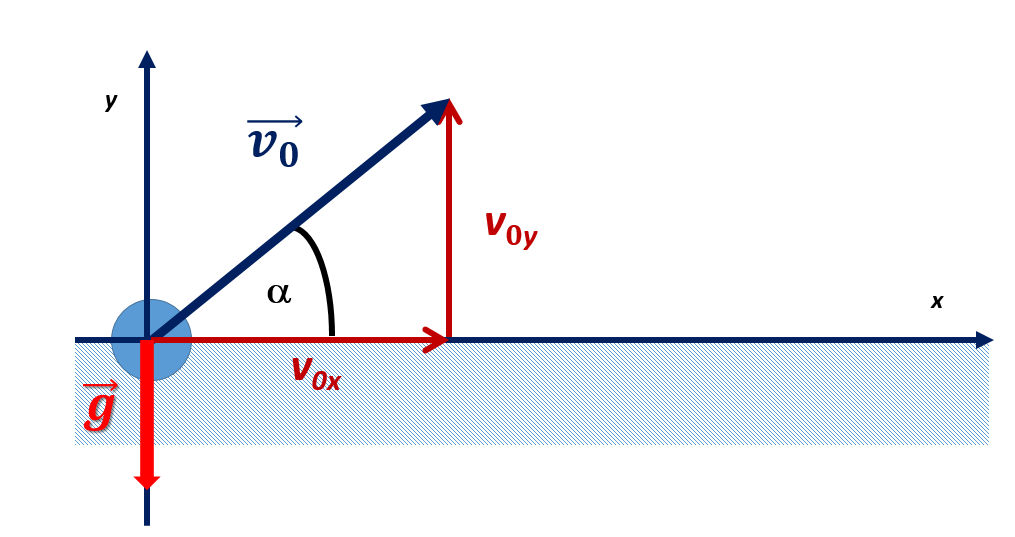
Vaatleme näiteks Maapinnalt horisondiga nurga α all kiirusega v0 kaldu visatud keha liikumist eeldusel, et kehale ei mõju õhutakistus (ainuke kehale mõjuv jõud on Maa raskusjõud st keha liigub vaba langemise kiirendusega g≈9,81 m/s2).
Taolise keha liikumisvõrrand (vektorkujul) on:
kus 
– keha asukohavektor (asukoht suvalisel ajahetkel); 
– keha algasukoha vektor (algasukoht); 
– keha algkiirus, 
– keha kiirendus (vaba langemise kiirendus) ning t – vaatlushetk.
Keha kiiruse võrrand (vektorvõrrand) aga
kus 
– keha kiirusvektor (kiirus suvalisel ajahetkel); – keha algkiirus, – keha kiirendus (vaba langemise kiirendus) ning t – vaatlushetk.
Lahutame liikumis- ja kiirusevõrrandid komponentideks (mooduliteks, koordinaatideks):
Leiame komponentide väärtused.
Algasukoht: x0=0; y0=0
Algkiirus: v0x=v0cosα; v0y= v0sinα
(Vaba langemise) kiirendus: gx=gcos270°; gy=gsin270°. NB! cos270°=0; sin270°=-1 à gx=0; gy=-g
Nii saame kiiruse koordinaatvõrranditeks:
ning liikumisvõrranditeks:
Võrranditest nähtub, et horisontaalsihis liigub taoline keha ühtlaselt, vertikaalsihis aga ühtlaselt muutuva kiirusega.
