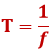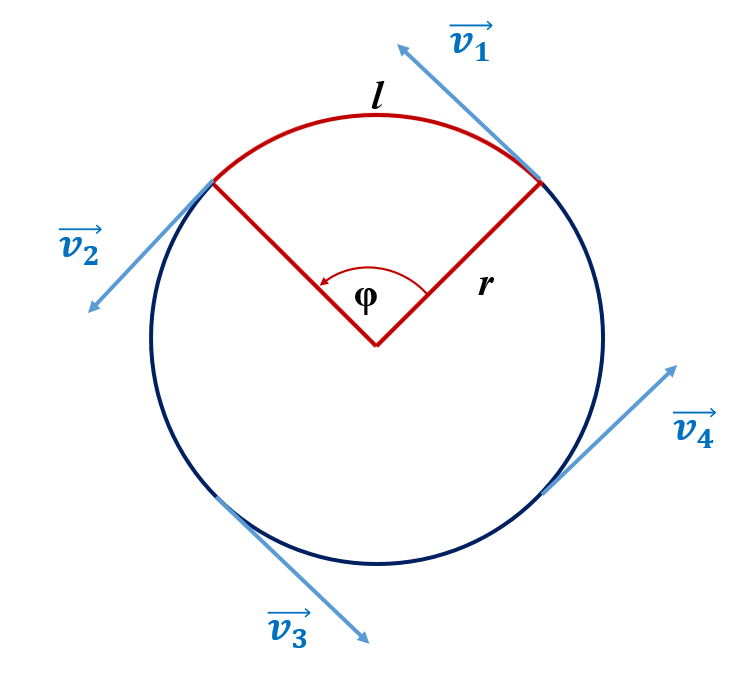
Ühtlaseks ringjooneliseks liikumiseks nimetatakse liikumist, kus keha liigub ringjoonelisel trajektooril ning tema kiiruse mooduli väärtus (joonkiirus) ajas ei muutu.
v1 = v2 = v3 = v4 = …
Tuleb rõhutada, et ringjooneliselt liikuva keha kiirus kui vektor muutub pidevalt, sest muutub kiirusvektori suund.
Ringjoonelise liikumise kirjeldamiseks kasutatakse pöördenurka φ – so kesknurk, mis jääb raadiuse algse ning pöördunud asendi vahele.
Pöördenurka mõõdetakse radiaanides. 1 radiaan on selline kesknurk, mille korral nurga haarade vahele jääva kaare pikkus on võrdne ringjoone raadiusega.
Nurkkiirus on füüsikaline suurus, mis iseloomustab keha trajektoori raadiuse poolt ajavahemikus Δt kaetavat pöördenurka φ:
Nurkkiirust mõõdetakse radiaanides sekundis: 1 rad/s
(Muutumatut) kiirust, millega keha liigub mööda ringjoone kaart nimetatakse keha joonkiiruseks (v). Keha poolt läbitud kaare (tee)pikkus l on võrdeline trajektoori raadiuse r ja pöördenurgaga φ:
Joonkiirus v on seega samuti võrdeline trajektoori raadiusega r ja nurkkiirusega 
:
Ajavahemikku, mille jooksul läbib keha ühe täisringi (teeb täispöörde), nimetatakse pöörlemisperioodiks (T).
Füüsikalist suurust, mis iseloomustab täispöörete arvu ajaühikus nimetatakse keha pöörlemissageduseks 
.
Ühe täispoorde korral kaetakse pöördenurk φ = 360° = π rad. Nii saame avaldada nurkkiiruse pöörlemissageduse f ja/või –perioodi T kaudu:
