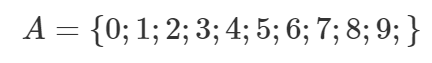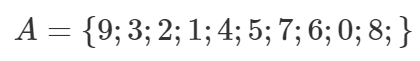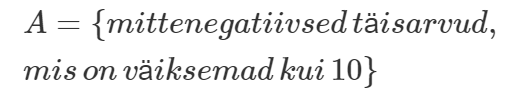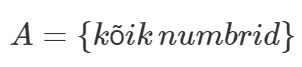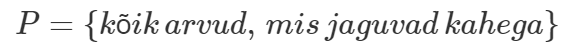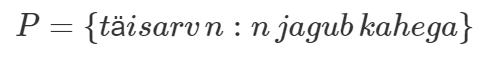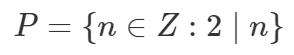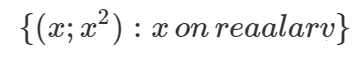Hulk
Nagu igapäevakeeleski, tähendab ka matemaatikute jaoks hulk mingite objektide kogumit. Näiteks moodustavad hulga kõik kartulid kastrulis, kõik õpilased klassis või kõik kassid vanaema keldris.
Hulgale kehtib ainult üks tingimus – ühedki kaks hulga elementi ei tohi olla võrdsed.
Matemaatikuid huvitavateks hulkadeks on näiteks kõikide naturaalarvude, negatiivsete reaalarvude, mingit võrrandit rahuldavate arvude või ka täisnurksete kolmnurkade hulk.
Hulkasid keskkoolis põhjalikumalt ei käsitleta – tegemist on ju nii lihtsate objektidega! Otsustasime siinkohal neist siiski rääkida, sest olgugi et lihtsad, on nad kogu matemaatika aluseks.
Hulkade kirjeldamine
Hulka kirjeldatakse tihti tema elemente loogeliste sulgude vahele üles loetledes. Näiteks kõik numbrid moodustavad hulga
Kuna igas lõigus ei ole mõtet kogu hulka välja kirjutada, antakse hulkadele tihti nimed. Enamasti tähistatakse hulkasid suurte tähtedega: näiteks võime öelda, et
Hulga elementidel puudub igasugune ambitsioon või kohustus end järjestada – nad on kõik võrdväärsed hulga liikmed. Seega oleksime võinud A elemendid loetleda ka mõnes muus suvalises järjekorras nagu näiteks
Hulka võib kirjeldada ka mõne tingimuse abil. Eeltoodud hulka oleksime näiteks võinud kirjeldada järgmiselt:
või lihtsalt
Paarisarvude hulka võime aga kirjeldada nii:
Lühendatult võib kirjeldus võtta ka järgmise kuju:
või kogenud matemaatikafänni kätetöös muutuda hoopis minimalistlikuks:
Seda avaldist peaks lugema järgnevalt: P on hulk, mis koosneb täisarvudest n nii, et n jagub kahega.
Andes hulgale A erinevaid kirjeldusi, kasutasime juba ühte lihtsat, aga tähtsat hulkade omadust: kaks hulka on võrdsed parajasti siis, kui neis on täpselt samad elemendid. Ehk teisisõnu hulgad on võrdsed parajasti siis, kui kõik elemendid, mis asuvad ühes hulgas, asuvad ka teises ning vastupidi.
Sulle võivad huvi pakkuda need õppematerjalid:
II kooliastme matemaatika reeglite kordamine
Numbrilised seosed
Peastarvutamine I kooliastmele
Liitmine 10 piires
Liitmine ja lahutamine 20 piires
8. klassi matemaatika teooriavideod
Üksliikmed, hulkliikmed ja tehted nendega
Liitmine ja lahutamine 10 piires
Hariliku murru kordamine
Ruutvõrrandi mõiste, ruutvõrrandi lahendivalem, ruutvõrrandi liigid
Protsendi rakendused igapäevaelus
Väike protsendiamps
Kirjalik liitmine
Algebralised murrud
Ruutvõrrandi abil lahenduvad tekstülesanded
Funktsioonid ja nende graafikud
Lahutamine 20 piires
Kirjeldav statistika
Geomeetria
Ruutjuur, tehted ruutjuurtega
Hulkade olulisus
Üritame järgnevalt vastata selle peatüki eksistentsiküsimusele: mis kasu on aga sellisest lihtsast objektide kogumist nagu hulk ja miks ta siia põhimõistete alla on sattunud? Veelgi enam, miks me räägime temast nii pikalt?
Tükkide sidumine
Esiteks koosneb peaaegu kõik väiksematest osadest. Nii võib peaaegu kõike juppideks lahti võtta ning nendejuppide abil kirjeldada. Näiteks pallivõistkond koosneb tema mängijatest, lause sõnadest, õhk erinevatest molekulidest, aatomituum prootonitest ja neutronitest ja nii edasi. Selliste kirjelduste taga võib juba näha hulkasid.
Sarnaselt tulevad hulgad mängu ka matemaatiliste objektide kirjeldamisel: näiteks ringjoont võib kirjeldada kui kõikide punktide hulka, mis asuvad ühest kindlast punktist – ringjoone keskpunktist – võrdsel kaugusel.
Just see alternatiivne kirjeldus selgitab, miks saame sirkliga ilusaid ringjooni joonistada. Kui asetame sirkli ühe haara ringjoone keskpunkti, siis liigutades teist haara joonistame järjest tollest keskpunktist võrdsel kaugusel olevaid punkte.
Korraga käitlemine
Teiseks tahame tihti midagi ette võtta paljude objektidega korraga.
Näiteks tahab õpetaja hinde panna kõikidele klassi õpilastele või mesilane tolmeldada kõiki ümbruskonna õienuppe. Nii võime rääkida hindamisest või tolmeldamisest kui operatsioonist, mida võib ette võtta kõikide õpilastega või kõikide õienuppudega.
Matemaatikas on hea, kui oskame iga kolmnurgaga seada vastavusse tema pindala või kõikide reaalarvude jaoks leida nende ruutude väärtuseid. Selliseid mõtteid saame täpselt ja matemaatiliselt kirja panna just hulkade abil, defineerides mingi tegevuse – või täpsemalt funktsiooni – kõikidel hulga elementidel.
Näiteks arvu ruutu võtmine on operatsioon, mis valib kõikide reaalarvude hulgast mõne arvu ning seab temaga vastavusse selle arvu korrutise iseendaga. See kõik on tihedalt seotud funktsioonidega ning nende niinimetatud määramis- ja muutumispiirkondadega [lk 67].
Hulgad on matemaatika aluseks
Kolmandaks – ja võibolla kõige üllatavamalt – osutuvad hulgad teatud mõttes kogu matemaatika aluseks.
Kui on rohkesti järjekindlust ja parasjagu kavalust, võib hulkade toel kirjeldada kõiki matemaatilisi objekte ja operatsioone. Nii ongi matemaatika seni kõige levinum vundament ehitatud just hulkadele. Kõik matemaatilised tulemused peaks teoreetiliselt saama ümber tõlkida keelde, kus ainsad objektid on hulgad ning nendega ümberkäimiseks on kümmekond karmi reeglit. See on oluline, kuna sellises keeles kirjutatud argumentide õigsust suudab kontrollida lisaks õpetajale juba ka arvuti – nii on igasugusel vaidlusel ots ja lõpp, arvuti teab täpselt! Tegelikult suudab arvuti juba isegi teatud lihtsamaid argumente sellises väga täpses ja formaalses keeles ka välja mõelda. Siiski on vähegi keerulisemate arutelude hulkade keelde ümber tõlkimine paras vaev ning matemaatikud on esialgu veel leidlikumad uute tulemuste tõestajad kui arvutid. Järgnevalt näitame, kuidas mõnda matemaatilist objekti hulkade abil kirjeldada. Meie raamatu piires neil kirjeldustel küll suurt olulisust pole, kuid võibolla on lihtsalt põnev lugeda.
Näiteks võib hulkade abil kirjeldada kõiki funktsioone [lk 64]. Ruutfunktsiooni – masinat, mis seab igale reaalarvule vastavusse tema ruudu – võime kirjeldada järjestatud arvupaaride hulgana:
Idee on siin mõelda, et iga arvupaari esimese liikmega seatakse vastavusse teine liige.
Kui vaatleksime funktsiooni y = x2 ainult täisarvude nullist seitsmeni, võksime kirjeldava hulga ka elementhaaval välja kirjutada:
Naljakal kombel on mõne lihtsama matemaatilise objekti kirjeldamiseks aga tarvis kauem mõelda. Näiteks kuidas kirjeldada arvu 4 ainult hulkade abil, arvudest rääkimata? Selleks on mitu viisi. Kirjeldame siin ühte võimalikku viisi.
Arv 1 seatakse vastavusse ilma ühegi elemendita tühja hulgaga: Ø. Tühjast hulgast võib mõelda kui tühjast kilekotist.
Arv 2 seatakse vastavusse hulgaga, mille ainsaks elemendiks on arvule 1 vastav hulk ehk tühihulk. Seega võime seda hulka kirjeldada sümbolites kui {Ø}. Oleme oma tühjale kilekotile ümber pannud veel ühe kilekoti – kokku kaks kilekotti.
Arv 3 seatakse vastavusse hulgaga, mille ainsaks elemendiks on arvule 2 vastav eelmises punktis leitud hulk. Tema kirjelduseks on {{Ø}}. Kilekott, mille sees on kilekott, mille sees on kilekott – kokku kolm kilekotti.
Arv 4 seatakse vastavusse hulgaga, mille ainsaks elemendiks on arvule 3 vastav hulk matemaatilise tähistusega {{{Ø}}} ehk neli kilekotti.
Nii võib muidugi jätkata ja kirjeldada kõiki naturaalarve 1, 2, 3, 4… hulkade või tõepoolest… kilekottide abil. Iga kilekoti lisamine ehk uue hulga tekitamine kandis endas arvu üks juurdeliitmise ideed.
Need on ainult kaks väljavalitud näidet, aga ka keerulisemaid objekte saab hulkadega esitleda. Selliselt mõeldes on hulgad ikka üsna ägedad: peaksid võimaldama kirjeldada kõike, mida matemaatikas teame.
Võibolla on tore ka teada, et tänaseks ei ole hulgad enam ainus kasutusel olev matemaatikale vundamendi ladumise viis. Kasutada võib ka teist tüüpi, pisut võimsamaid objektide kogumeid – kategooriaid. Kategooria ei koosne enam üksnes erinevatest objektidest, vaid sisaldab ka seoseid nende objektide vahel.
Hulgad ja peavalu
Hulgad on matemaatikutele ka paradokside näol palju peavalu toonud.
20. sajandi algupoolel tekitas pahandust inglise filosoof ja matemaatik Bertrand Russell järgmise lihtsa küsimusega: kas mõni hulk võiks olla ka iseenda element?
Võibolla arutles ta umbes nii.
Kui mul on hulga koostamiseks vabad käed, võin ju nõuda, et minu hullumeelse hulga iga element oleks selline hulk, mis ei ole iseenda element.
Kas sel juhul mu hullumeelne hulk ise on enda elemendiks?
Kui ta oleks enda element, siis ta peaks olema selline hulk, mis ei ole iseenda element – huhuu, päris vastuoluline!
Kui ta aga on selline hulk, mis ei ole iseenda element,siis ta peaks vastupidi just kuuluma hullumeelsesse hulka ehk olema iseenda element! Ka vastuoluline!
Ma ei saagi sellele küsimusele vastata, katastroof!
Katastroof või mitte, mõtteainet pakkus see paradoks paljudele. Lõpuks leiti ka lahendus – igasugu kummaliste paradokside vältimiseks ei tohi lihtsalt lubada täielikult vabu käsi hulkade koostamisel.
Üldiselt selle üle aga muretsema ei pea – kõik hulgad, millest koolimatemaatikas räägitakse, on tõepoolest ka kõige karmimate nõuete järgi matemaatilised hulgad. Võib vahest lihtsalt meelde jätta, et ka alguses väga lihtsad ja selged mõisted võivad enda varjus peita igasuguseid riukaid.
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!