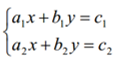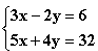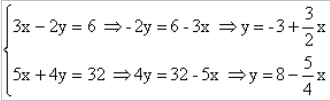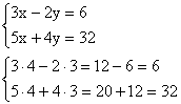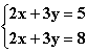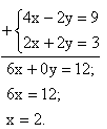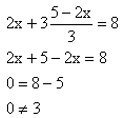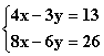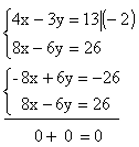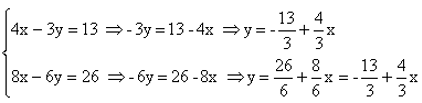KAHE TUNDMATUGA LINEAARVÕRRANDISÜSTEEMI LAHENDAMINE
Kui kaks lineaarvõrrandit (kahe tundmatuga) moodustavad võrrandite paari, siis otsime nende võrrandite ühist lahendit. Selleks lahendatakse võrrandisüsteem, mille kuju on:
Siin x ja y on tundmatud (ehk muutujad ehk otsitavad) ja arvud a, b ja c on arvud.
Võrrandisüsteeme saab lahendada liitmisvõttega, asendusvõttega ja graafiliselt.
Sulle võivad huvi pakkuda need õppematerjalid:
Numbrilised seosed
Liitmine ja lahutamine 20 piires
Peastarvutamine I kooliastmele
Üksliikmed, hulkliikmed ja tehted nendega
xy-koordinaatsüsteem
Peastarvutamine eelkoolile
Kirjalik liitmine
Ruutvõrrand
Lahutamine 20 piires
Harjutusülesandeid matemaatika riigieksamiks
Kell ja kellaaeg
Ruutjuur, tehted ruutjuurtega
II kooliastme matemaatika reeglite kordamine
Väike protsendiamps
Kirjalik lahutamine
Ruumilised kujundid
Tasandilised kujundid
Protsendid põhikooli matemaatikas
Ruutvõrrandi abil lahenduvad tekstülesanded
8. klassi matemaatika teooriavideod
Liitmisvõte
Liitmisvõtte kasutamiseks teisendatakse võrrandeid nii, et ühe muutuja kordajad oleksid teineteise vastandarvud. Seejärel liidetakse võrrandid ülevalt alla ja saadakse võrrand ainult ühe tundmatu suhtes.
Saime y väärtuseks -6. Leiame x väärtuse, asendades saadud y väärtuse ühte esialgsesse võrrandisse.
Võrrandisüsteemide puhul tuleb teha ka kontroll, asendades saadud väärtused mõlemasse esialgsesse võrrandisse. Lahendid on õiged, kui oleme saanud võrrandite vasakud ja paremad pooled sama väärtusega.
Asendusvõte
Asendusvõttega lahendamiseks avaldame ühest võrrandist ühe muutuja ja siis asendame saadud tulemuse teise võrrandisse.
Saime kätte muutuja y väärtuse. Asendame selle võrrandisse 1.
Graafiline lahendamine
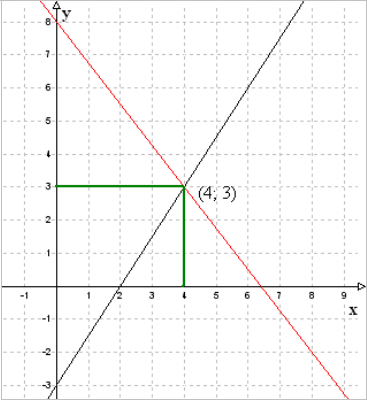
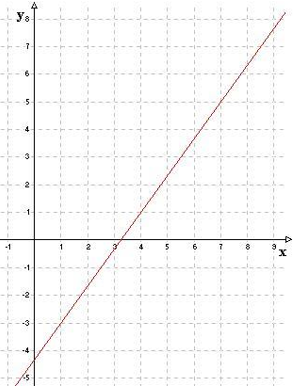
Graafiliseks lahendamiseks leiame mõlema võrrandi jaoks kaks punkti, mida need sirged läbivad (anname x-le väärtuse ja arvutame y välja), kanname need joonisele ja ühendame sirgeks. Saadud sirgete lõikepunkt on lahendiks (näide pärit www.kool.ee).
Lahenda võrrandisüsteem:
1. Selleks visandame koordinaatteljestikku mõlemad graafikud. Graafiku tegemiseks on vaja teha väärtuste tabel. Kuna tegu on esimese astme võrrandiga, mille graafikuks on sirge, siis piisab kahest punktist. Teeme selleks väiksed teisendused.
Teeme graafiku:
Graafikul sirgete lõikepunkt (4; 3) ongi võrrandisüsteemi lahendiks.
Kontroll:
Alati tehke kontroll! Selleks asendame võrrandisüsteemis olevad tundmatud nende arvuliste väärtustega ja vaatame, kas võrdused on tõesed.
Vastus: Arvupaar x = 4 ja y = 3 on antud võrrandisüsteemi lahendiks.
- Näited võrrandisüsteemidest, millel lahend puudub või on lõpmatult palju lahendeid.
Näide 1. Lahenda võrrandisüsteem:
Lahendus:
Avaldame ühest võrrandist ühe tundmatu teise kaudu (asendusvõte), näiteks esimesest võrrandist muutuja y muutuja x kaudu.
Me leiame ainult selle y väärtuse, mis on ühine mõlemale võrrandile ja seepärast asetame saadud y avaldise teise võrrandisse:
Saime ühe tundmatuga esimese astme võrrandi, mida lahendades saame:
Sellel võrrandisüsteemil lahendeid ei ole, kuna 3 ei saa mitte kunagi võrduda nulliga.
Seda ülesannet oleks saanud ka lihtsamalt lahendada. Kuna võrrandisüsteemi võrrandite vasakud pooled on võrdsed, kuid paremad pooled mitte, siis järelikult süsteemil puudub lahend.
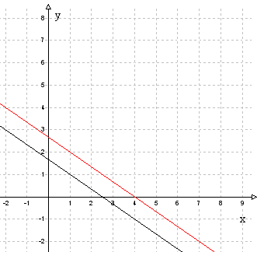
Graafiliselt:
Must on esimene võrrand, punane teine. Nagu näha, on tegu paralleelsete sirgetega, millel puuduvad lõikepunktid.
Vastus: Sellel võrrandisüsteemil lahend puudub.
Näide 2. Lahendada võrrandisüsteem:
Lahendus:
Äärmiselt lihtne on kasutada siin liitmisvõtet.
See võte seisneb selles, et mõlemas võrrandis teisaldatakse ühe ja sama tundmatu kordajad absoluutväärtuselt võrdseiks, aga märgilt vastupidisteks. Seejärel liidetakse võrrandite vastavad pooled ning saadakse ühe tundmatuga võrrand. Meie korrutame võrrandisüsteemi esimest võrrandit arvuga –2 ning seejärel liidame teisele võrrandile.
Sellisel juhul on lahendeid lõpmata palju. Mida see tähendab? Kui teeme nende kahe võrrandi järgi graafiku, siis etteruttavalt olgu öeldud, et mõlema võrrandi sirged ühtivad.
Teeme selleks väiksed teisendused.
Ehk siis graafikul
Vastus: Sellel võrrandisüsteemil on lõpmatu hulk lahendeid.
Testid võrrandisüsteemide peale:
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!