TRAPETS
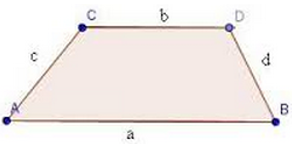
Trapetsiks nimetatakse nelinurka, mille kaks külge on paralleelsed ja kaks mitteparalleelsed.
Trapetsi paralleelseid külgi nimetatakse alusteks ja mitteparalleelsed küljed on trapetsi haarad.
Trapetsi omadused:
- alused on paralleelsed
- trapetsi haara lähisnurkade summa on 180°
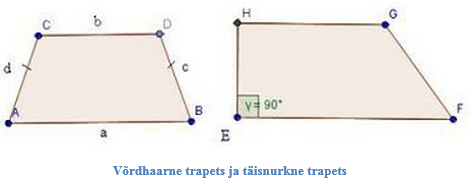
Trapetsit, mille haarad on võrdsed, nimetatakse võrdhaarseks trapetsiks.
Võrdhaarse trapetsi omadused:
Sulle võivad huvi pakkuda need õppematerjalid:
Allar Veelmaa videotund. Avaldised
Hariliku murru kordamine
Numbrilised seosed
Ratsionaalavaldised
Ruutjuur, tehted ruutjuurtega
8. klassi matemaatika teooriavideod
Kirjalik liitmine
Kell ja kellaaeg
Ruutvõrrandi abil lahenduvad tekstülesanded
Funktsioonide graafikud
Väike protsendiamps
Kirjalik lahutamine
Väike algebraamps
II kooliastme matemaatika reeglite kordamine
NUPUTAME KOOS! Tasapinnalised kujundid
Lahutamine 20 piires
Peastarvutamine eelkoolile
Liitmine ja lahutamine 20 piires
Tasandilised kujundid
Ruutvõrrandi mõiste, ruutvõrrandi lahendivalem, ruutvõrrandi liigid
- haarad on võrdsed
- aluse lähisnurgad on võrdsed
- diagonaalid on võrdsed
Trapetsit, mille üks haar on risti alustega, nimetatakse täisnurkseks trapetsiks.
Täisnurkse trapetsi omadused:
- trapetsi lühem haar on risti alustega ja selle haara lähisnurgad on 90°.
Trapetsi ümbermõõt ja pindala
ÜMBERMÕÕT:
Kuna trapetsi küljed on üldjuhul kõik erineva pikkusega, siis ümbermõõt P = a + b + c + d.
PINDALA:
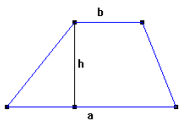
Trapetsi pindala võrdub aluste poolsumma ja kõrguse korrutisega ![]()
Trapetsi kesklõik
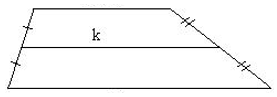
Lõiku, mis ühendab trapetsi haarade keskpunkte, nimetatakse trapetsi kesklõiguks.
Trapetsi kesklõik on alustega paralleelne ja võrdub aluste poolsummaga.
Seega saab trapetsi pindala leida ka valemiga ![]()
Trapetsi liigid
- Kui trapetsi haarad on võrdsed, siis nimetatakse trapetsit võrdhaarseks.
Võrdhaarse trapetsi lähisnurgad on võrdsed.
- Kui üks haaradest on risti alusega, siis nimetatakse trapetsit täisnurkseks.
Sel juhul on üks haar võrdne kõrgusega.
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!