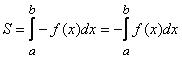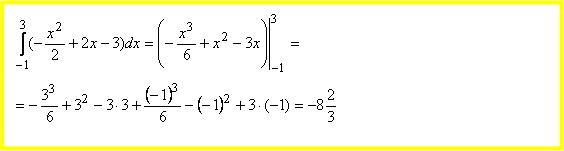Kõvertrapets allpool x-telge
Olgu antud pidev funktsioon f(x)<0 lõigus [a;b].
Järelikult
Integreerides lõigus [a;b] funktsiooni f(x)<0, saame vastava (allpool x-telge asuva) kõvertrapetsi pindala vastandarvu. Seega allpool x-telge asuva kõvertrapetsi pindala saamiseks tuleb võtta integraali absoluutväärtus või vahetada integreerides rajad.
Sulle võivad huvi pakkuda need õppematerjalid:
Ruutjuur, tehted ruutjuurtega
Kirjalik liitmine
Peastarvutamine eelkoolile
Protsendi rakendused igapäevaelus
NUPUTAME KOOS! Tasapinnalised kujundid
xy-koordinaatsüsteem
Tasandilised kujundid
Ruumilised kujundid
Kirjalik lahutamine
Väike protsendiamps
Ruutvõrrandi mõiste, ruutvõrrandi lahendivalem, ruutvõrrandi liigid
Geomeetria
Hariliku murru kordamine
Liitmine ja lahutamine 10 piires
Kell ja kellaaeg
Üksliikmed, hulkliikmed ja tehted nendega
Funktsioonid ja nende graafikud
Liitmine ja lahutamine 20 piires
Ruutvõrrandi abil lahenduvad tekstülesanded
Lahutamine 20 piires
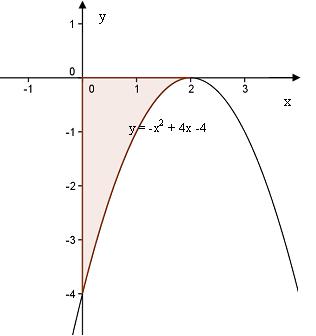
Leia joonisel värvitud kõvertrapetsi pindala.
Vastus: 
Näide:
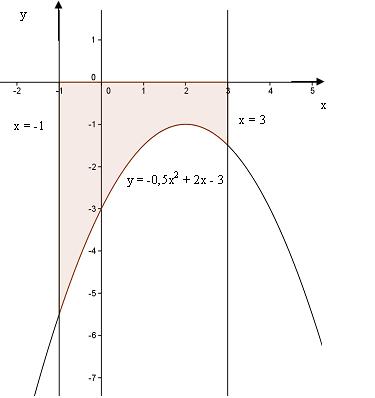
Leia kõvertrapetsi pindala, mida piiravad jooned y = -0,5x2 + 2x – 3, x = -1, x = 3 ja y = 0
Kui kõvertrapets asub allpool x-telge, siis on pindalaks määratud integraali absoluutväärtus. Selle arvutamiseks võib aga ka vahetada rajad.
Kui me arvutaksime rajades -1st kuni 3-ni, saakisime tulemuseks negatiivse arvu.
Pindala aga ei saa olle negatiivne. Proovi lahendada sama ülesannet, vahetades rajad.
Vastus: Kõvertrapetsi pindala on 
pindalaühikut.
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!
