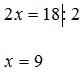VÕRRE. VÕRDE PÕHIOMADUS. VÕRDEKUJULISE VÕRRANDI LAHENDAMINE
Võrdeks nimetatakse tõest võrdust, mille mõlemad pooled on jagatised.
Valem: 
ehk 
Muutujad a, b, c ja d on võrde liikmed. Võrde esimene liiget a ja viimane liiget d nimetatakse võrde välisliikmeteks ning teine liige b ja kolmas liige c on võrde siseliikmed.
Võrret, mis sisaldab tundmatut, nimetatakse võrdekujuliseks võrrandiks.
Sulle võivad huvi pakkuda need õppematerjalid:
Üksliikmed, hulkliikmed ja tehted nendega
II kooliastme matemaatika reeglite kordamine
Liitmine ja lahutamine 20 piires
Funktsioonid ja nende graafikud
Ruutvõrrand
Ruutvõrrandi abil lahenduvad tekstülesanded
Liitmine 10 piires
Hariliku murru kordamine
Kell ja kellaaeg
Ruutvõrrandi mõiste, ruutvõrrandi lahendivalem, ruutvõrrandi liigid
Peastarvutamine eelkoolile
Lahutamine 20 piires
Tasandilised kujundid
Protsendid põhikooli matemaatikas
Kirjalik lahutamine
Liitmine ja lahutamine 10 piires
Ruumilised kujundid
Geomeetria
xy-koordinaatsüsteem
Väike protsendiamps
Näide: 
Selliseid võrdekujulisi võrrandeid lahendatakse võrde põhiomaduse abil.
Võrde põhiomadus ütleb, et võrde välisliikmete korrutis on võrdne tema siseliikmete korrutisega.
Valem: Võrde puhul kasutame võrde põhiomadust ja saame 
Näide: Lahendame võrde .
Võrde põhiomadust kasutades saame, et 
.
Edasi lahendame kasutades võrrandi omadusi.
Saime lahendiks arvu 9.
Kontroll: vasak pool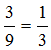 
, parem pool 
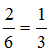. Saime, et vasak pool on võrdne parema poolega.
Vastus: lahend on 9.
Lisaks:
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!
