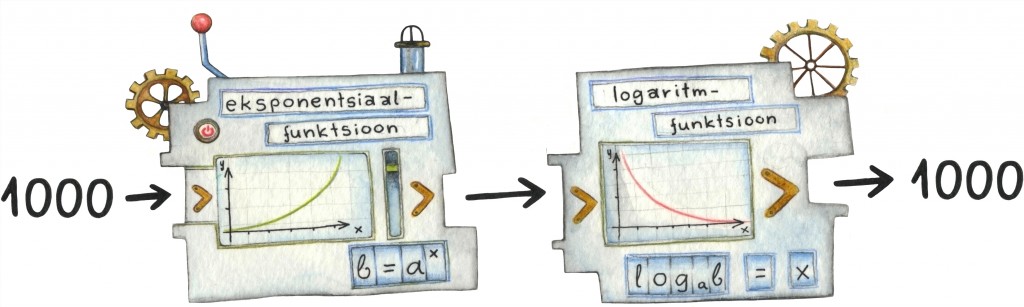
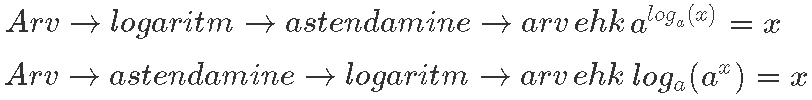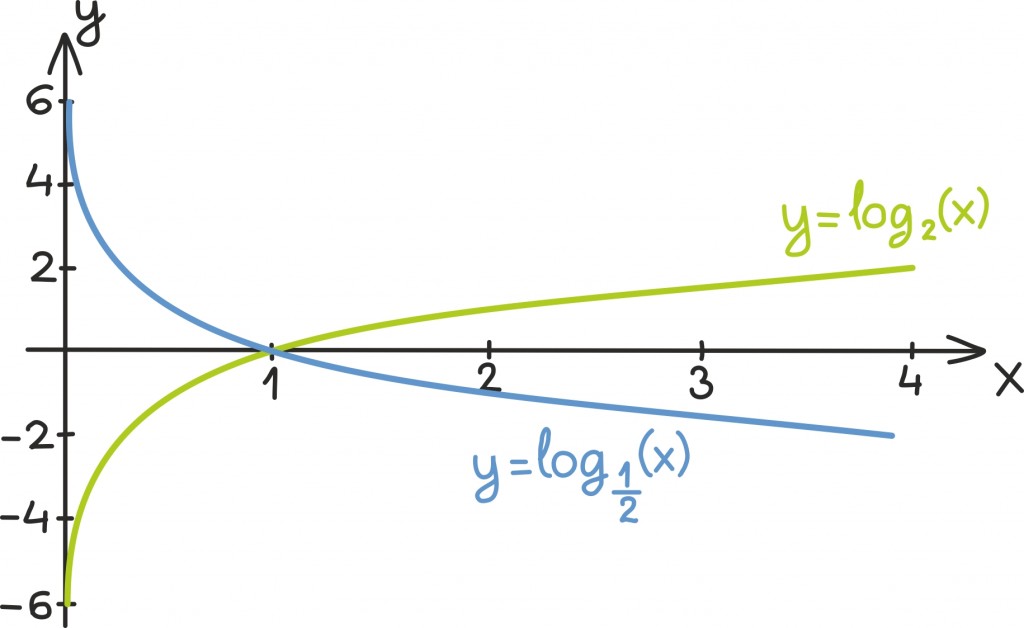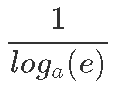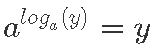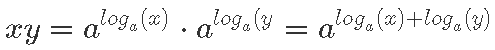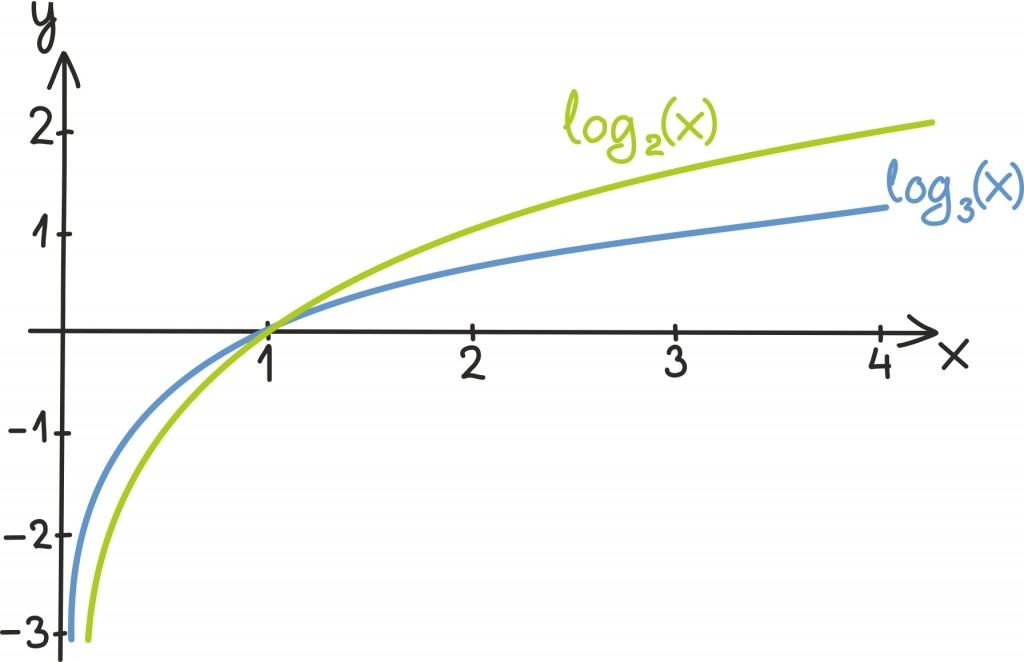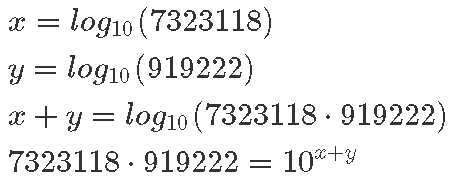Logaritm
Logaritm on eksponentsiaalfunktsiooni pöördfunktsioon [lk 69] ehk teisisõnu, kui järjest rakendada arvule 1000 kõigepealt eksponentsiaalfunktsiooni mingil alusel ning siis logaritmfunktsiooni samal alusel, saame jälle tulemuseks sama arvu: 1000.
Intuitiivselt tähendab see järgmist. Meenutame, et eksponentsiaalfunktsiooniga kirjeldame kasvavaid suuruseid. Söötes talle ette teatava ajahetke, saame vastuseks kasvava suuruse väärtuse selleks hetkeks. Logaritm vastab aga vastupidisele küsimusele: kui kaua võtaks aega, et eksponentsiaalne kasvuprotsess jõuaks ühe või teise suuruseni?
Näiteks oletame, et panete oma vaevaga kogutud 1000 eurot panka kasvama ning pangas makstakse intressi 5% aastas.
Kuna iga aasta möödudes suureneb summa täpselt 1,05 korda, võime summa kasvamist kirjeldada eksponentsiaalfunktsiooni abil:
Logaritm vastab aga küsimusele, mitu aastat läheb aega, et sellest algsummast kasvaks 10 000 eurot ehk summa kümnekordistuks. Teisisõnu küsib logaritm sellist x-i väärtust, mille jaoks
ehk
Matemaatiliselt kirjutatakse see välja nii:
Vastus on muuseas 47,2 aastat…
Logaritmfunktsioon
Oletame, et meile on antud mingi alus a > 0, a ≠1 nagu eksponentsiaalfunktsiooni korralgi. Kui ay = x, siis kirjutame loga(x) = y ja loeme, et logaritm arvustx alusel a on y. Kolm sümbolit järjest! Näiteks kuna 25 = 32, siis log2(32) = 5 ehk logaritm arvust 32 alusel 2 on 5.
Logaritmfunktsiooni alusel a saame nüüd, kui vaatamegi arvu x funktsiooni sisendina. Ei ole muidugi kohe päris selge, mis loom see logaritmfunktsioon ikka on ning mis väärtuste jaoks ta on üldsegi defineeritud.
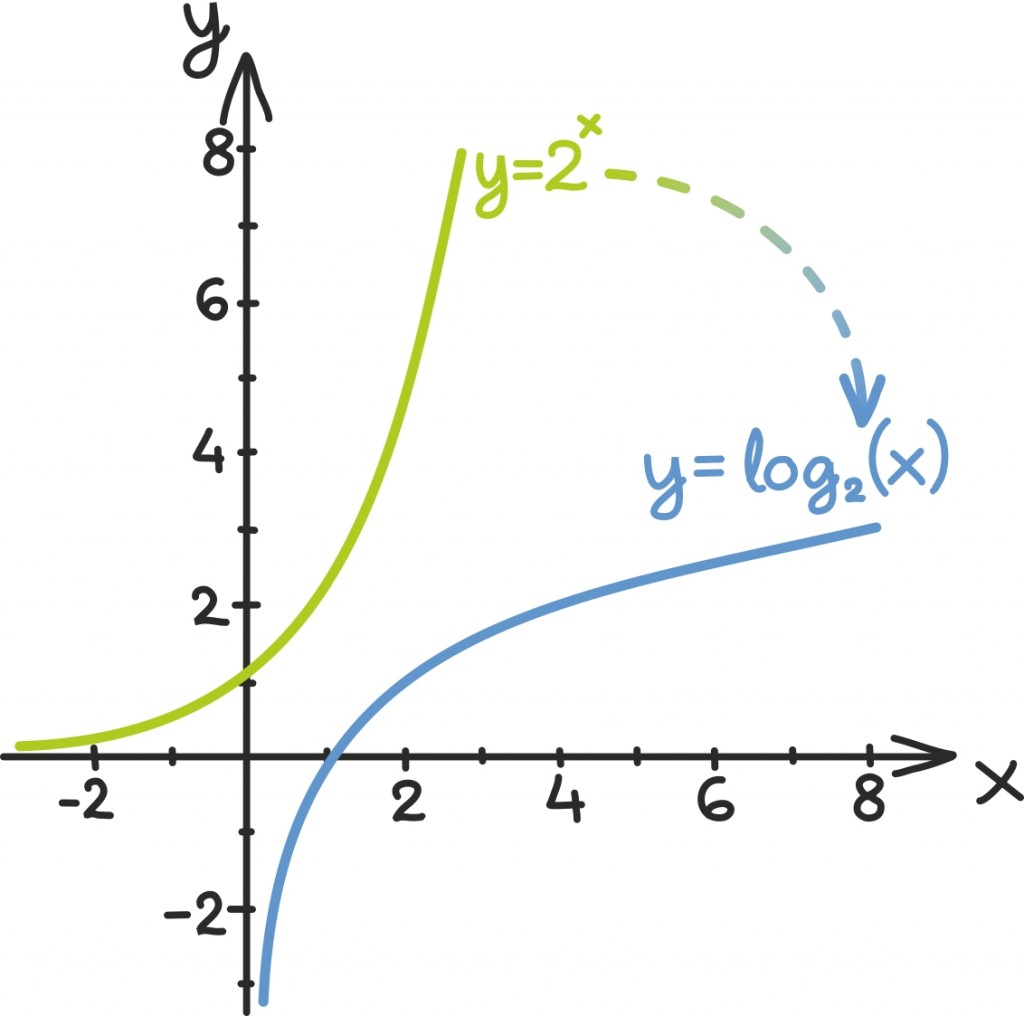
Ilusam on võibolla mõelda geomeetriliselt. Nimelt kuna logaritmfunktsioon on eksponentsiaalfunktsiooni pöördfunktsioon, võib teda kirjeldada eksponentsiaalfunktsiooni enda graafiku abil.
Kui joonistame koordinaattasandile eksponentsiaalfunktsiooni y = ax graafiku, siis saame logaritmfunktsiooni alusel a lihtsalt siis, kui x– ja y-teljed ära vahetame. Nagu juba nägime, võib sellest mõelda ka kui eksponentsiaalfunktsiooni graafiku peegeldamisest sirgest y = x.
Graafikult näeme, et logaritmfunktsioon on kenasti defineeritud kõikide positiivsete reaalarvude jaoks – põhjuseks on muidugi see, et eksponentsiaalfunktsiooni väärtused saavad olla ainult positiivsed arvud.
Võib tekkida ka teine küsimus: miks me nõudsime, et alus a peab olema positiivne? Vastus tuleneb eelmisest peatükist: eksponentsiaalfunktsioon ise on defineeritud ainult positiivsete aluste korral. Negatiivsete alustega tekkis ju teadupärast probleeme: näiteks ei oska me reaalarvude raames võtta arvu –4 ruutjuurt ehk tõsta teda astmele 0,5. See on küll võimalik, tuues sisse kompleksarvud [lk 89], aga praegu tahaksime, et meie funktsioonid võtaksid nii sisendina kui annaksid ka väljundiks ainult reaalarve.
Sulle võivad huvi pakkuda need õppematerjalid:
Liitmine ja lahutamine 10 piires
Lahutamine 20 piires
Ruumilised kujundid
Üksliikmed, hulkliikmed ja tehted nendega
Allar Veelmaa videotund. Avaldised
Kirjeldav statistika
Ruutvõrrand
Tasandilised kujundid
Ruutvõrrandi abil lahenduvad tekstülesanded
II kooliastme matemaatika reeglite kordamine
Kirjalik liitmine
Numbrilised seosed
Väike protsendiamps
Ratsionaalavaldised
Peastarvutamine eelkoolile
xy-koordinaatsüsteem
Liitmine 10 piires
Protsendid põhikooli matemaatikas
Funktsioonide graafikute lõikepunktide leidmine
Peastarvutamine I kooliastmele
Logaritm: tehe või funktsioon?
Logaritm tuleb mõnikord lisaks funktsioonile esile ka tehete kontekstis, kui temast räägitakse kui logaritmimisest. See võib alguses üllatav tunduda, aga tihti võib mõnest matemaatilisest objektist või teisendusest mõelda mitut moodi.
Näiteks ka astendamisest võisime mõelda kui tehtest või kui funktsioonist. Tehtest rääkisime peatükis arvu aste – valisime arvu a ja arvu b ning andsime tähenduse arvu astmele ab – kahest arvust meisterdasime kokku ühe kolmanda. Eelmises peatükis aga fikseerisime astendamise aluse a ja rääkisime hoopis eksponentsiaalfunktsioonist ax – masinast, mis võttis sisendiks reaalarve ja andis vastu positiivseid reaalarve.
Samamoodi võime logaritmimisest mõelda kui tehtest: kui valime positiivse reaalarvu a logaritmi aluseks ning mingi arvu b, siis võime võtta logaritmiloga(b). Niipea, kui aga oleme otsustanud fikseerida mõne aluse, näiteks kahe, võime vaadelda funktsiooni y = log2(x).
Muidugi ei piirdu näited ainult astendamise ja logaritmimisega, lugeja võib veenduda, et ka näiteks liitmisest võime mõelda nii tehete kui funktsioonide raames. Selline paindlikkus on matemaatikale üsna omane – mida rohkem vaatevinkleid, seda rohkem võimalusi.
Ka selles peatükis käsitleme logaritmi nii ühes kui teises võtmes.
Logaritmfunktsiooni omadused
Kõige olulisem on vahest logaritmfunktsiooni juures see, et tegemist on eksponentsiaalfunktsiooni pöördfunktsiooniga. Oleme seda juba mitu korda öelnud, aga sõnastame selle veel korra ümber ka skemaatilis-matemaatiliselt!
Logaritmfunktsiooni võime võtta kõikidest positiivsetest reaalarvudest. Väärtustena annab ta lahkelt vastu kõikvõimalikke reaalarve. Ka logaritmfunktsiooni käitumine sõltub tema alusest. Näiteks logaritmfunktsioonid alusel 2 ja alusel ½ on teineteise peegeldused x-telje suhtes:
Põnev on ka meenutada, et eksponentsiaalfunktsiooni korral tuli aluse pöördarvuks muutmisel funktsiooni peegeldada hoopis y-teljest. Oskad seda mustrit selgitada?
Ka logaritmfunktsioon on kenasti pidev. Vaadeldes natuke tema graafikut näiteks ühest suurema aluse korral, näeme, et logaritmfunktsioon küll kasvab piiramatult, aga järjest aeglasemalt.
Tõepoolest, logaritmfunktsiooni kasvu kiirust näitav tuletis on antud funktsiooniga kujus
ning see on suurte x väärtuste korral nullist juba üsna eristamatu.
Konstandi b väärtus sõltub logaritmfunktsiooni alusest, näiteks kui aluseks on e, on b võrdne ühega nagu eelneval joonisel.
Muudel juhtudel on selleks konstandiks
kus a on logaritmi aluseks. Miks see nii on, selgitame juba varsti logaritmi erinevate aluste peatükis.
Korrutamisest liitmine
Kui eksponentsiaalfunktsioon tegi liitmisest korrutamise, siis logaritmfunktsioon teeb korrutamisest liitmise. Kuna tegemist on eksponentsiaalfunktsiooni pöördfunktsiooniga, pole seda muidugi raske uskuda. Enda täielikuks veenmiseks võib aga näiteks läbi teha järgneva arutelu.
- Kuna logaritmfunktsioon ja eksponentsiaalfunktsioon on pöördfunktsioonid, siis
- Samamoodi aga ka
ja
- Eksponentsiaalfunktsioon teeb aga korrutamisest liitmise: seega
Kokkuvõttes saame, et
Kas sellest järeldub ka kohe, et loga(xy) = loga(x) + loga(y)? Päris automaatselt ei järeldu, peame oleme ettevaatlikud. Näiteks teame ju, et ruutu võtmisel annavad 3 ja –3 sama tulemuse, ja seega kui teaksime, et a2 = b2, ei saaks me järeldada, et a =b.
Õnneks on eksponentsiaalfunktsiooni korral olukord lihtsam. Nägime eksponentsiaalfunktsiooni graafikult, et tegemist on kas rangelt kasvava või rangelt kahaneva funktsiooniga ja seega ei võta ta ühtegi väärtust mitu korda. Seega kui teame, et ax = ay, võime järeldada, et x = y. Nii võime sellest, kui
tõesti ka järeldada, et
Logaritmi erinevad alused
Nagu eksponentsiaalfunktsiooni korral, on ka logaritmfunktsiooni iseloom alusest sõltuvalt natuke erinev. Samas on ka logaritmfunktsiooni aluse vahetamine päris lihtne ja analoogne eksponentsiaalfunktsiooni puhul toimunuga.
Nimelt oletame, et meile on antud mingi arvu ylogaritm alusel 3. Tähistame seda x = log3(y) ning võime võrdväärselt ka kirjutada 3x = y. Kuidas nüüd üle minna alusele 2?
Eksponentsiaalfunktsiooni peatükis nägime, et võime arvu 3 kirjutada arvu 2 astmena, ehk 2w = 3. Edasi saame kirjutada
See tähendab täpselt, et log2(y) = wx. Aga me teame juba, et x = log3(y) ning samas puhtalt definitsioonistw = log2(3).
Seega saame log2(y) = log3(y) · log2(3) ehk logaritmfunktsiooni alusel 2 saame lihtsalt, kui korrutame logaritmfunktsiooni alusel 3 ühe kindla arvuga. Selle arvu võime leida: log2(3) ≈ 1,58 ning log2(x) ≈ 1,58 · log3(x).
Üldkujus astme vahetamist, üleminekut aluselt aalusele b iseloomustab valem:
Jällegi tähendab see ainult, et astme vahetamiseks korrutame logaritmfunktsiooni lihtsalt läbi ühe teatava arvuga – arvuga logb(a). Seetõttu jõuame pisut ehk üllatavale järeldusele: erinevatel alustel logaritmfunktsioonid on äärmiselt sarnased, võime alustada logaritmfunktsioonist alusel 2 ja saada kõik teised logaritmfunktsioonid seda funktsiooni lihtsalt nullist erineva arvuga läbi korrutades.
Millist alust valida?
Ka seekord on teatud olukordades mõne alusega kergem ja mugavam ringi käia, eriti kui sõna saavad ka loodusteadlased ja arvutimehed. Logaritm mingil alusel a muutub oluliseks, kui vaadeldav „suurusjärk” ehk olulised erinevused suurustes on määratud arvu a kordsetega.
Päriselus ja füüsikas teeme arvutusi kümnendsüsteemis. Loomulikud suurusjärgud on ühelised, kümnelised, sajalised ehk siis kümnekordsed. Seega on mugav kasutada ka logaritme alusel 10.
Kui aga näiteks töötame kahendsüsteemis, on kõik arvud antud kahe astmete summana ehk oluline muutus toimub arvude kahega korrutamisel. Nii on ka loomulik suurusjärk kaks ning loomulik logaritmimine käibki alusel kaks. Kuna arvutid teevad kõike kahendsüsteemis, tuleb ka logaritm alusel kaks ehk log2x esile just arvutitega tegelemisel.
Logaritmi alusel e nimetatakse naturaallogaritmiks ning teda tähistatakse vahel ka loge(x) asemel lihtsalt ln(x)-ga. Nagu nimest võib aimata, on temaski midagi loomulikku ja ilusat.
Arvust e oleme juba rääkinud nii ilusate arvude peatükis [lk 102] kui äsja eksponentsiaalfunktsiooni juures. Temaga on tore koostööd teha.
Logaritmi tähendus arvutusajaloos
Logaritmid on ajalooliselt panustanud tublisti ka loodusteaduste ja eriti just astronoomia arengusse: nad võimaldasid juba enne arvutite leiutamist inimestel korrutada suuri ja keerulisi arve.
Logaritmide abi oli nii määrav, et uhke astronoom ja matemaatik Laplace oli omal ajal logaritmidest lausa joovastuses: „Imetlusväärne nõks, mis taandab mitme kuu töö vaid mõnele päevale, kahekordistades nõnda astronoomi elu ja hoides teda pikkade arvutustega kaasnevatest vigadest ja tülgastusest.” Kust see kõik tuleb?
Kõige motiveerivam on ilmselt veidi peast arvutada: 7323118 · 919222!
Õudus! Mida küll teha sellise tehtega? Tänapäeval on muidugi väga lihtne: võtad pinginaabri kotist taskuarvuti või nutitelefoni ja arvutus saab pärast mitut ebaõnnestunud katset siiski tehtud. Võib ka pikalt ja kirjalikult korrutama hakata, aga see võtab mõistuspäratult aega ja pole ei põnev ega lõbus.
17. sajandil ei olnud astronoomidel veel taskuarvuteid, kuid nende arusaam lõbust polnud sugugi nii palju erinev: neilegi ei meeldinud pikki ja igavaid arvutusi teha. Ometigi oli taevakehade liikumises tihti vaja korrutada suuri ja kosmiliselt suuri arve. Appi tuli logaritm.
Kuidas logaritm siis arvutusi lihtsustas?
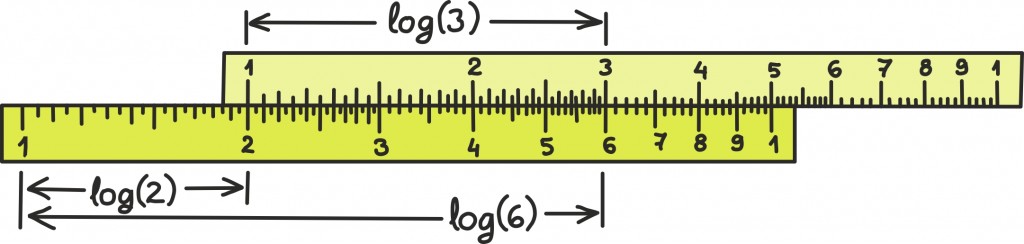
Logaritmi idee arvutuste lihtsustamisel peitub tema kuulsas omaduses teha korrutamisest liitmine: log(ab) = log(a) + log(b).
Nii taandame korrutamise liitmisele ja liita on ju määratult lihtsam.
Kuidas siis näiteks korrutada omavahel 7323118 ja 919222?
Võtame kõigepealt mõlemast arvust logaritmid alusel 10, seejärel liidame need logaritmid kokku ning kasutame tulemust 10 astendamisel:
Kaks esimest tehet on muidugi võimalikud, kuna logaritmfunktsioon on igal alusel määratud kõikide positiivsete reaalarvude korral.
Tulemuse saamiseks piisaks nüüd ühest suurest tabelist. Esiteks peaks sealt saama piisava täpsusega järele vaadata arvude logaritme ehk kuidas neid esitada kümne astmena – näiteks 7323118 juures oleks kirjas 6,864 ning 919222 juures 5,963. Teiseks peaks sealt leidma ka vastupidist teavet: iga arvu x jaoks astme 10x väärtuse – näiteks 5,001 koha peal oleks kirjas 10023. Muidugi ei saaks tabelis olla lõpmatult palju arve ja seega peaksid kõik arvud tabelis olema antud mingi teatava täpsusega, näiteks kolme või nelja komakohaga.
Nii võiksime oma arvutuse teha väga kiirelt. Alustuseks leiaksime tabelist arvud 6,864 ja 5,963, siis liidaksime nad, et saada 12,827, ning viimaks vaataksime tabelist järele arvu 1012,827 väärtuse: 6 714 000 000 000. Kuna päris vastus on 6 731 571 174 196, näeme, et meie täpsus on nõnda üsna talutav.
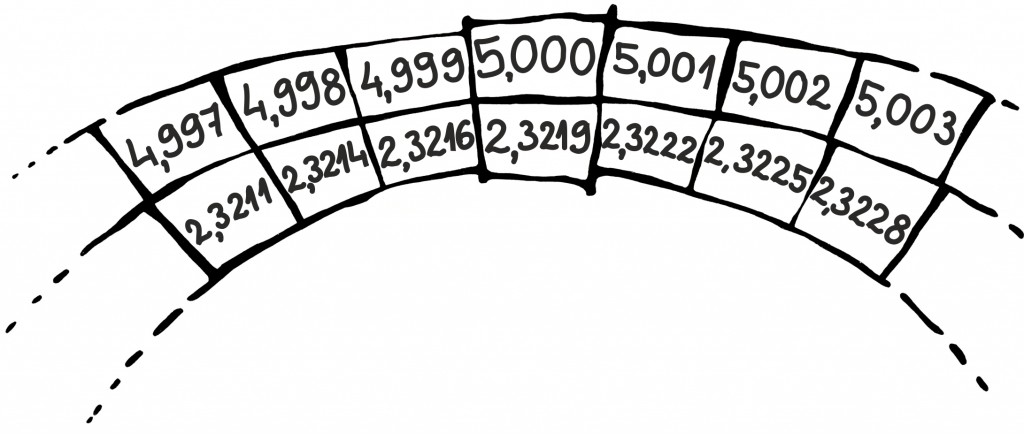
Muidugi pidid logaritmitabelid olema kavalalt kokku pandud, et sinna mahutada võimalikult palju arve. Võid ise näha, kui pikaks läheks tabel, kui lihtsalt laduda ühte ritta arvud ja teise nende logaritmid:
Ülemisel real oleme edasi liikunud seitsme lahtriga ainult 0,006 võrra! Joonisel asuv tabel on küll tõesti avatud hoopis teiselt kohalt ja on ka hoopis teisel alusel, aga see suurt ei muuda. Muuseas, võibolla nuputad välja, mis aluse jaoks see tabel on?
Siiski on ka suurtest arvutabelitest vaatlemine ja ise kokku liitmine tüütu ning peatselt peale logaritmi leiutamist tuldi lagedale veel kavalama idee ja riistapuuga. Selle nimeks on lükati ja teda kasutati veel 20. sajandi keskpaigaski, niikaua kui taskuarvutid ta välja puksisid.
Korrutamist lihtsustaval lükatil on arvud paigutatud kavalalt, logaritmskaalalisel kaugusel ja nii võib korrutamistehtega ühele poole saada lihtsalt lükati ülemist hooba alumise suhtes liigutades. Näiteks antud joonisel on omavahel korrutatud 2 ja 3. Suure täpsuse jaoks joonistati skaaladki ülitäpsed. Räägitakse, et observatooriumites kasutati tähtsamateks arvutusteks mitmemeetriseid lükateid ning skaalasid uuriti samal ajal mikroskoobiga.
Logaritmiline skaala
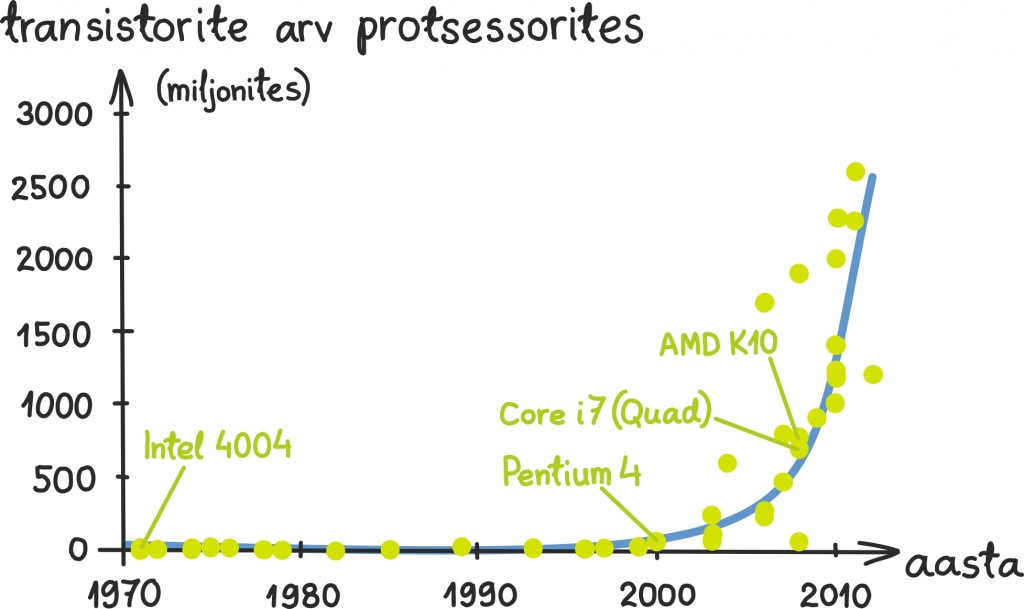
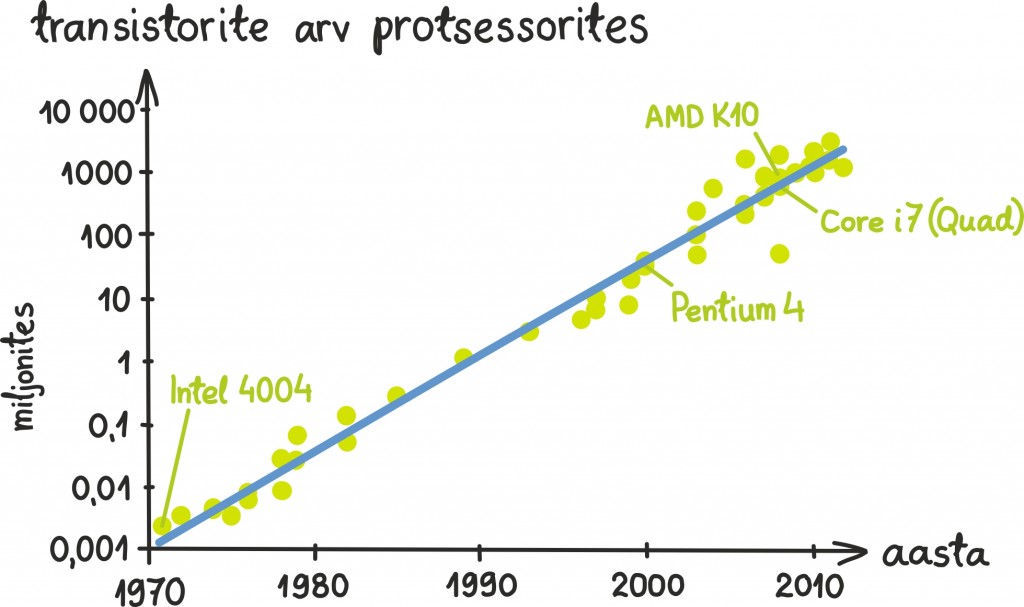
Kui soovime mingeid andmeid graafiliselt kujutada, ei olegi arvtelgedel tavalise skaala kasutamine alati parim valik. Tavalise ehk lineaarse skaala all peame siis silmas seda, et ühikud vertikaalteljel muutuvad ühtlaselt, nagu näiteks eelmises peatükis transistorite arvu tutvustaval graafikul:
Kuigi kõik nägi väga kena välja, on suurem osa protsessoritest tegelikult üsna eristamatult nulljoone külje all. Probleem on selles, et ettetulevad suurused erinevad mitu suurusjärku ja lineaarne skaala jääb lihtsalt liiga kitsaks. Mingis mõttes toimus transistorite arvu areng mitte liitmise, vaid korrutamise teel. Seda saab ka graafiliselt kujutada, võttes appi arvude kujutamise logaritmilisel skaalal. Sel juhul tähendab iga ühikuline samm vertikaalteljel tervet suurusjärgu muutumist – jällegi liitmise asemel korrutame.
Näiteks kasutades transistorite arvu esitamiseks logaritmilist skaalat, on pilt palju ilusam ja ülevaatlikum:
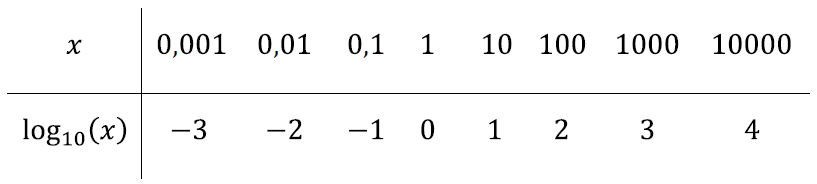
Logaritmiliseks nimetatakse seda skaalat seetõttu, et logaritmimise suhtes muutuvad vertikaaltelje ühikud jällegi ühtlaselt, nagu kombeks. Tõepoolest, meenutades kümnendlogaritmi tähistust, võime vertikaaltelje skaala ümber tõlkida järgmise tabeli abil:
Maavärinad
Logaritmilised skaalad on kasutusel ka paljude nähtuste hindamiseks, mis võivad esineda väga erinevates suurusjärkudes.
Ka maavärinate tugevust mõõdetakse logaritmilisel skaalal. Seda skaalat kutsutakse pidulikult tema kasutusele võtja järgi Richteri skaalaks. Lihtsustatult näitab maavärina tugevus Richteri skaalal, kui mitu suurusjärku võimsam on värinaga kaasnenud maakoore võnkumine maakoore tavapärasest võnkumisest.
Kuna Richteri skaala kasutab kümnendlogaritmi, tähendab iga lisapall tegelikult 10 korda suuremat maavärinat.
Väikseid maavärinaid on päris palju: maavärinaid, mille suurus on 3 kuni 4 palli, juhtub üle 10 000 korra aastas. Neid maavärinaid on nõrgalt tunda, aga õnneks need tavaliselt purustusi ei tekita. Maavärinad, mis on 1000 korda suuremad ehk 6 kuni 7 palli, on nõrgematele majadele hävitava jõuga sadade kilomeetrite raadiuses ja neid juhtub maakeral keskmiselt iga kolme päeva tagant. Üle 9 palli maavärinaid juhtub paar korda sajandis ning nende läheduses ei jää enam püsti ükski maja.
Suurim maavärin, mille tugevust on mõõdetud, juhtus Tšiilis 1960. aastal. Tema võimsuseks oli lausa 9,5 palli – seega oli ta isegi purustavatest 6- kuni 7-pallistest maavärinatest veel 1000 korda võimsam. Selle asemel, et õudustele mõelda, mõtle hoopis, kui seda kõike peaks kirjeldama lineaarse skaalaga – 9 palli asemel peaksime näiteks kasutama arvu 1 000 000 000.
Kuidas paigutada punkte arvteljele
Joonista endale arvtelg. Pane kuskile kirja nullpunkt ja kuskile punkt 100. Kuhu paigutaksid arvu 20?
Koolitunnis kasutame arvteljel peaaegu alati lineaarset skaalat: kui arvude vahed on võrdsed, on võrdsed ka nendevahelised kaugused arvteljel. Seda mõttelaadi järgides peaksid arvu 20 paigutama viiendikule 0 ja 100 vahelisest kaugusest.
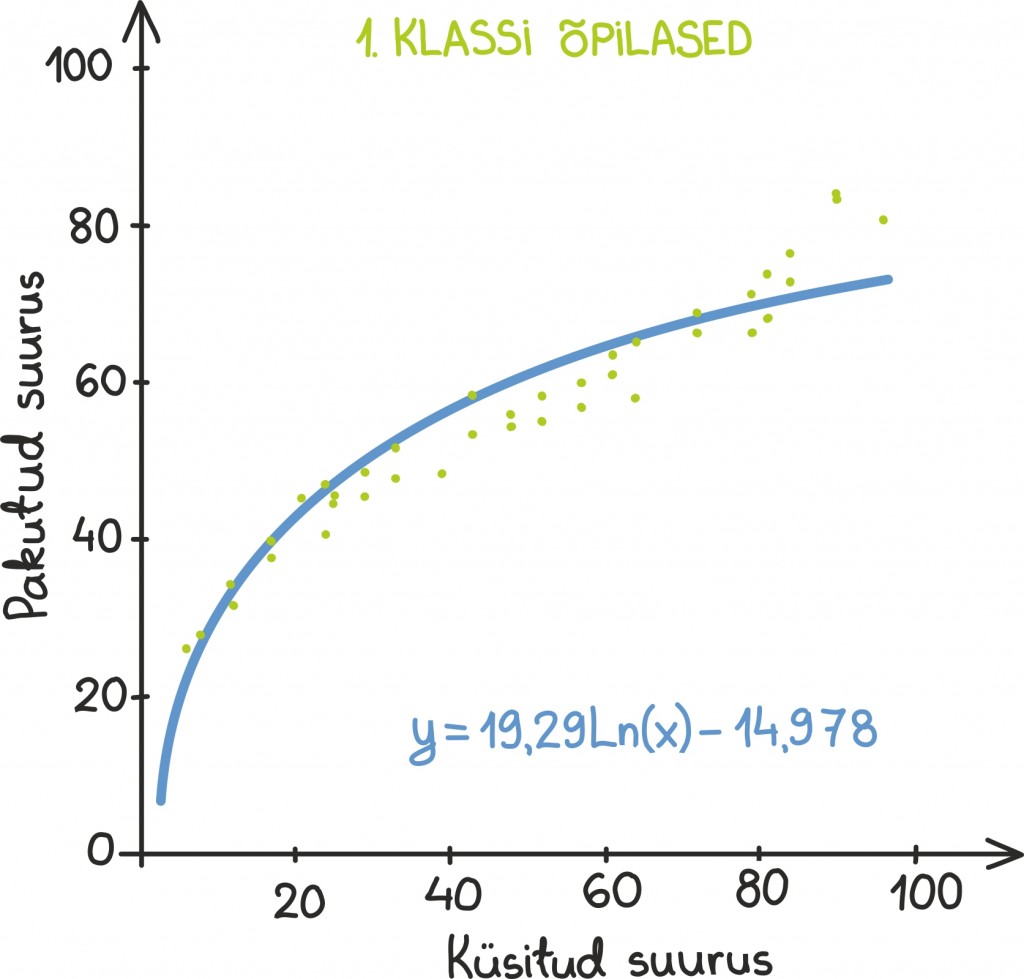
Selgub siiski, et see ei olegi võibolla meile kõige loomuomasem valik. Näiteks on leitud, et esimese klassi juntsud paigutavad arvu 20 arvteljel palju kaugemale kui meie. Umbes siia:
Leidmaks selle paigutuse tagant mingit loogikat, paluti lastel arvteljele seada ka paljusid teisi arve. Selgus, et üldine komme on jätta väiksematele arvudele rohkem ruumi kui suurematele. Täpsem uurimine näitas, et arvteljel kasutatud kaugus sõltub arvu enda suurusest logaritmiliselt ehk teisisõnu lapsed kasutasid arvteljel hoopis logaritmilist skaalat!
Seda valikut saab võibolla ka natuke intuitiivselt selgitada. Nimelt tundub ju, et arvude 87 ja 88 erinevus on vähem tähtis kui arvude 2 ja 3 erinevus. Mõõtes arvude vahet mitte absoluutselt, vaid suhteliselt, on see tunne ka igati täpne: 87 on 88-st umbes 1,01 korda suurem, aga 3 arvust 2 tervelt 1,5 korda suurem. Selline suhtelise erinevuse kasutamine tookski näiteks endaga kaasa logaritmilise skaala.
Kuidas joonistada logaritmilist skaalat?
Oleme üritanud selgitada, et logaritmiline skaala on kasulik, laialt kasutatav ja tore. Aga kuidas seda ise joonistada? Kõige lihtsam on muidugi anda ülesanne mõnele andmetöötlusprogrammile – ütled neile logaritmiline skaala ja ongi valmis.
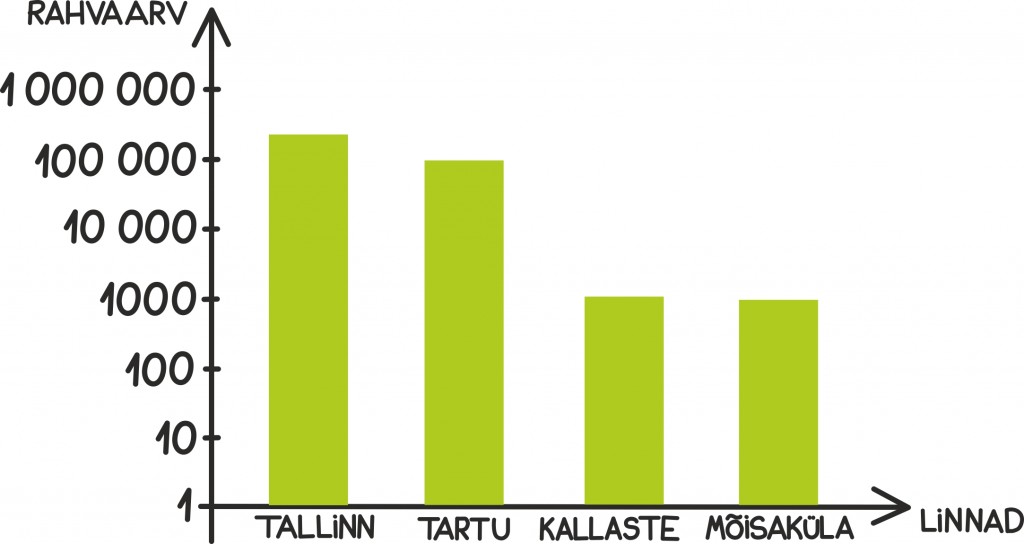
Järgnevalt mõtiskleme, kuidas seda käsitsi teha, ja selle jaoks vaatleme näiteks võrdlevalt Eesti linnade suurust.
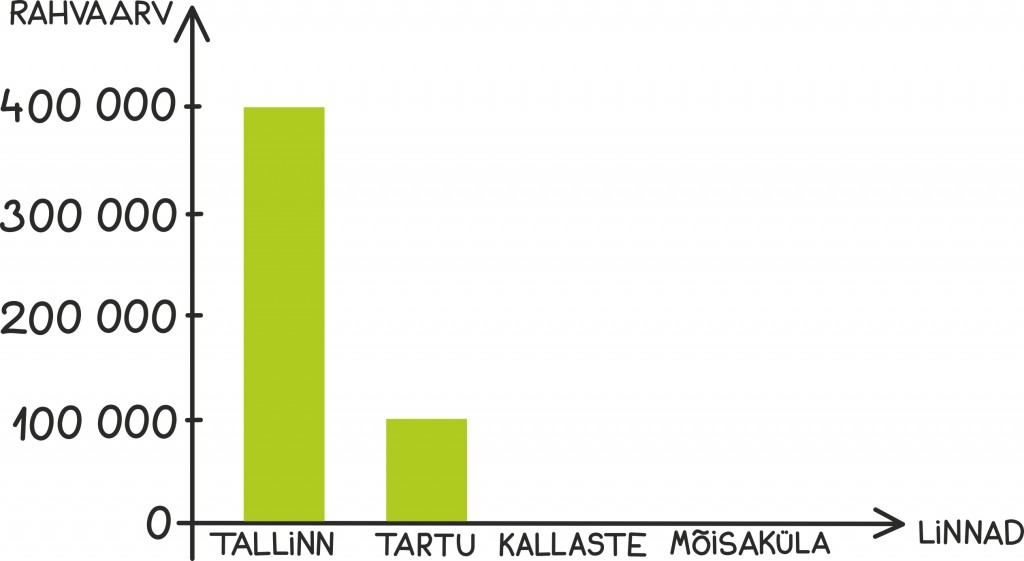
Kas saaksime kuidagi ühele graafikule kanda nii Eesti kõige rohkem kui kõige vähem rahvastatud linnad? Nende linnade rahvaarv varieerub tuhandest inimesest kuni peaaegu poole miljonini: Tallinn 400292, Tartu 103740, Kallaste 1106 ning Mõisaküla 1002.
Tavaline, lineaarne skaala meid jällegi väga ei aita. Kuna vertikaalteljel on ühtlane samm, siis mahuvad pildile kas ainult väikesed linnad või mahub Tallinn ja väiksemaid linnu polegi näha. Tuhandese sammu korral peaksime ju liikuma 400 ühikut ülespoole, et ka Tallinna leida!
Nagu ennist juba rääkisime, peaks logaritmiline skaala seda olukorda parandama, sest seal tähendab iga samm ülespoole hoopis korrutamist.
Logaritmilise skaala joonistamiseks peame esmalt fikseerima sammu suuruse ehk mis arvuga me ülespoole liikudes korrutame. Populaarsed valikud on 10 ja 2, aga täpne valik sõltub eelkõige kontekstist – mis suurusjärkudes tegelikult suuruseid võrrelda tahame. Praegu võtamegi selleks suhtarvuks kümne.
Nüüd hakkame vertikaaltelje samme nimetama 10 astmete abil, iga edasine samm tähendab kümnega korrutamist. Kuskilt tuleb alustada ja linna rahvastiku kokkulöömisel võime alustada näiteks arvust 1 = 100.
Järgmine samm vertikaalteljel viiks rahvaarvu 10 korda suuremaks, seega järgmise joone juurde kirjutame juba 10. Veel üks ühik edasi tähendaks juba arvu 100 ja nii edasi, iga sammuga ikka kümme korda suuremaks. Kõnealusel juhul, kuna üheski linnas pole rohkem kui miljon elanikku, jätkame veel neli sammu, kuni miljonini välja. Saame järgneva graafiku:
Kui nüüd lisame suurimate ja väikseimate linnade rahvaarvu kujutavad tulbad, siis näeme hoopis ilusamat pilti. Samale graafikule mahuvad nii suurimad kui väikseimad linnad:
Niisiis, logaritmiline graafik ei ole sugugi keerulisem kui tavaline graafik, ent mõnikord palju ülevaatlikum. Vertikaalsel teljel tuleb siis liitmise asemel lihtsalt korrutada.
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!