Sündmuse suhteline sagedus. Statistiline tõenäosus
Absoluutne ja suhteline sagedus
Buku saarel on 28 kirjaoskamatut inimest, kõrvalasuval Muku saarel aga 280 kirjaoskamatut. Mida me nende andmete kohta oskame öelda? Kas võib öelda, et Buku saarel on enam-vähem kõik kirjaoskajad ja Muku saarel ei oska peaaegu keegi lugeda?
Paraku ei saa nende andmete põhjal mingeid järeldusi teha, sest me ei tea kummalgi saarel elavate inimeste arvu. Oletame, et Buku saarel elab 29 inimest ja Muku saarel 12005 inimest. Sel juhul väljendavad arvud 28 ja 280 absoluutset sagedust, s.t. seda, kui palju on kummalgi saarel kirjaoskamatuid, kuid saareelanike kirjaoskuse kirjeldamiseks on olulisem suhteline sagedus, s.t kui mitu protsenti kummagi saare elanikest lugeda ei mõista.
Buku saarel on kirjaoskamatuid ![]() ja Muku saarel
ja Muku saarel ![]() . Selle näite põhjal on lihtne veenduda, et absoluutse sageduse põhjal ei saa teha üldistusi.
. Selle näite põhjal on lihtne veenduda, et absoluutse sageduse põhjal ei saa teha üldistusi.
Sulle võivad huvi pakkuda need õppematerjalid:
II kooliastme matemaatika reeglite kordamine
Üksliikmed, hulkliikmed ja tehted nendega
Lahutamine 20 piires
Liitmine ja lahutamine 10 piires
Peastarvutamine I kooliastmele
Kell ja kellaaeg
Tasandilised kujundid
Kirjalik lahutamine
Numbrilised seosed
Funktsioonide graafikute lõikepunktide leidmine
Ruutvõrrandi mõiste, ruutvõrrandi lahendivalem, ruutvõrrandi liigid
xy-koordinaatsüsteem
Peastarvutamine eelkoolile
Funktsioonide graafikud
Liitmine 20 piires
Ruutvõrrandi abil lahenduvad tekstülesanded
Ruutvõrrand
Ruutjuur, tehted ruutjuurtega
Harjutusülesandeid matemaatika riigieksamiks
Liitmine ja lahutamine 20 piires
Kokkuvõttes:
absoluutne sagedus – arv m, mis näitab, kui mitu korda sündmus katseseerias toimus;
suhteline sagedus – sündmuse esinemiste arvu m jagatis katsete koguarvuga n
Kuidas jaotuvad täringu veeretamisel saadud silmad?
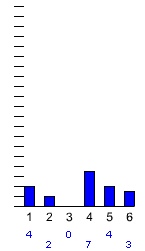
Võtame täringu ja veeretame kümme-kakskümmend korda, seejuures märgime üles iga kord saadud silmade arvu. Nii tekkinud tabel on sagedustabel. Tekib küsimus – kas täringuveeretamisel saadud silmade arvu suhteline sagedus allub mingile seaduspärasusele? Uurige järgnevalt Marti poolt tehtud katseid ja tehke järeldus.
Marti teab, et täringuheitel on 1, 2, 3, 4, 5 või 6 silma saamine võrdse tõenäosusega ja see on ![]() . Kas see tähendab, et kui täringut kuus korda heita, siis ilmuvad kõik silmad täpselt ühe korra välja? Marti otsustas teha täringutega katsed.
. Kas see tähendab, et kui täringut kuus korda heita, siis ilmuvad kõik silmad täpselt ühe korra välja? Marti otsustas teha täringutega katsed.
Vasakpoolsel joonisel on katsetulemused peale täringu kahtekümmet heidet. Marti ei usu oma silmi – kolm silma pole tulnud välja mitte ühtegi korda. Kas sellest saab järeldada, et kolm silma ei tule üldse välja.
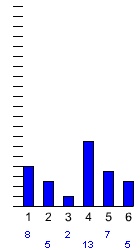
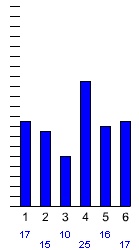
Marti jätkas katset. Ta heitis täringut 40 korda, 100 korda ja lõpuks 10000 korda.
Näeme, et mida rohkem täringuid heita, seda väiksemaks jäävad erinevused erinevate silmade esiletuleku arvude vahel. Eriti hästi on see näha kolme silma heitmise puhul. Esimesest kahekümnest katsest on suhteline sagedus 0, neljakümne heite puhul 2/40 = 0,05 ning saja heite puhul juba 10/100 = 0,1. Viimases katses on see 1661/10000 = 0,1661 ehk ligikaudu 1/6.
Marti tegi järelduse: küllalt pika katseseeria korral on sündmuse suhteline sagedus ligikaudu võrdne selle sündmuse tõenäosusega ühel katsel.
Suhtelise sageduse omadused. Statistiline tõenäosus
Natuke ajaloost
Klassikalise tõenäosuse tulemusi saab kontrollida statistilise tõenäosuse meetoditega. “Kulli ja kirja” heitmisel teame, et nii kulli kui ka kirja saamise tõenäosus on täpselt 1/2. Kui aga münti heita ja seejuures katsetulemused üles märkida, siis võib juhtuda ka nii, et esimesest kümnest heitest ei saa me üle kahe-kolme “kulli”. Seega on tegemist sama nähtusega, nagu eespool kirjeldatud Marti poolt läbiviidud katses.
Prantsuse teadlane Georges Buffon viskas münti 4040 korda ja sai 2048 kulli, inglise matemaatik Karl Pearson viskas münti 24000 korda ja sai 12012 kulli.
Lugege Georges Buffoni ja Karl Pearsoni kohta ka Wikipeedia artikleid: