PÖÖRDVÕRDELINE SÕLTUVUS, PÖÖRDVÕRDELISE SÕLTUVUSE GRAAFIK
Kui kahe muutuja vastavate väärtuste korrutis on jääv, nimetatakse nendevahelist seost pöördvõrdeliseks sõltuvuseks.
Öeldakse, et funktsiooni y väärtused on pöördvõrdelises seoses muutuja x vastavate väärtustega.
See tähendab, et ühe muutuja väärtuste suurenemisel (vähenemisel), väheneb (suureneb) teise muutuja väärtus sama arv korda.
Sulle võivad huvi pakkuda need õppematerjalid:
Kirjalik liitmine
Protsendid põhikooli matemaatikas
Protsendi rakendused igapäevaelus
Funktsioonide graafikute lõikepunktide leidmine
xy-koordinaatsüsteem
NUPUTAME KOOS! Tasapinnalised kujundid
Tasandilised kujundid
Valik harjutusülesandeid matemaatika riigieksamiks
Ruumilised kujundid
Väike protsendiamps
Numbrilised seosed
Ruutjuur, tehted ruutjuurtega
Kell ja kellaaeg
II kooliastme matemaatika reeglite kordamine
Kirjalik lahutamine
Algebralised murrud
Liitmine ja lahutamine 10 piires
Allar Veelmaa videotund. Avaldised
Hariliku murru kordamine
Liitmine ja lahutamine 20 piires
Pöördvõrdelise seose graafikut nimetatakse hüperbooliks.
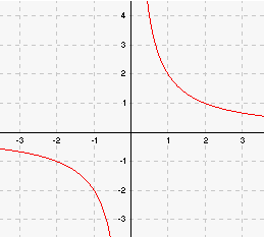
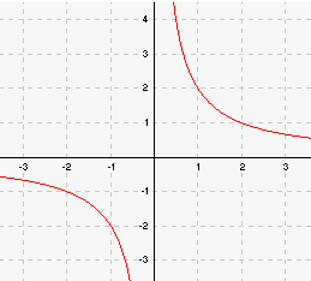
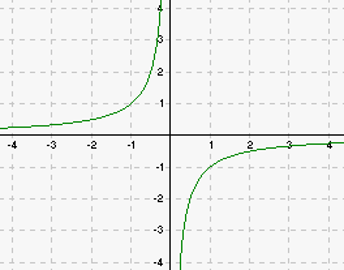
Kui pöördvõrdelise seoses a>0, siis asub graafik koordinaattasandi I ja III veerandis, kui a<0, siis II ja IV veerandis.
Alloleval joonisel (Joonis 1) on kujutatud pöördvõrdelise seose 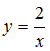 graafik.
graafik.
Alloleval joonisel (Joonis 2) on kujutatud pöördvõrdelise seose ![]() graafik.
graafik.
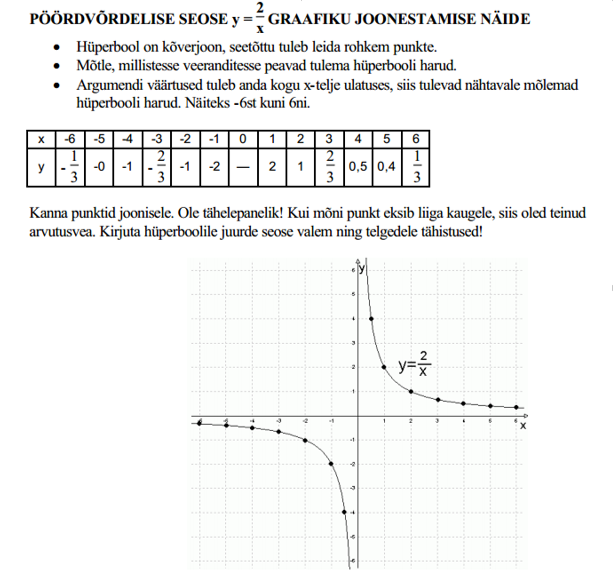
Pöördvõrdelise seose graafiku joonestamise näide:
TESTID:
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!