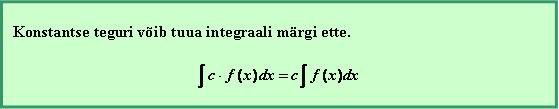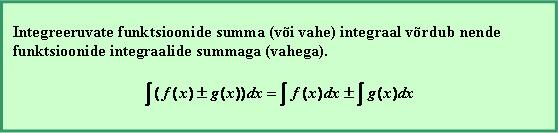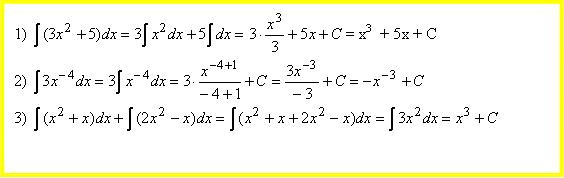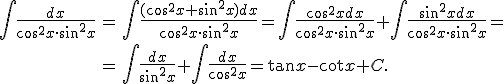Määramata integraali omadused
1. Konstandiga korrutatud funktsiooni integreerimine:
2. Summa või vahe integreerimine:
Viimast valemit võib kasutada ka vastupidi.
Näide:
Allikas: Integraal/Omadused
Omadus 1. Määramata integraal kahe või mitme funktsiooni algebralisest summast (vahest) võrdub liidetavate integraalide summaga (vahega):
Omadus 2. Konstantse teguri võib tuua integraalimärgi ette, st kui 
on reaalarve, siis
Funktsiooni määramata integraali leidmist vahetult omaduste 1 ja 2 ning integreerimise põhivalemite abil nimetatakse vahetuks integreerimiseks.
Näide 1. Leia integraal vahetu integreerimese teel.
Lahendus. Omaduste 1 ja 2 põhjal saame
kus kõigi kolme integraali kohta kirjutasime ühe suvalise konstandi C.
Toome mõne näite integreerimise kohta, kus integreeritav funktsioon teisendatakse erinevate teisendustega tabeliintegraalideks.
Lahendus. Lisame lugejale ja lahutame lugejast ühe ja sama arvu 1:
Kui on tegemist trigonomeetria funktsioonidega, siis on mõnikord otstarbekas kasutada järgmisi valemeid:
Näidis: leia järgmised integraalid
Lahendus. Et 1=cos²x+sin²x, siis
Allikas:
