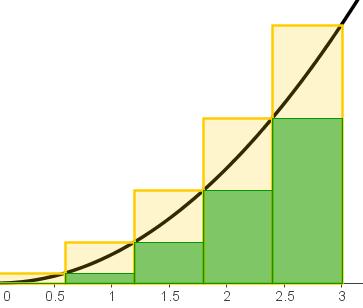
Kõvertrapets.Ristkülikute meetod
Kõigepealt vaatame, kuidas leidis kõvertrapetsi pindala Archimedes (287 – 212 eKr). Ta uuris, kui suure osa ühikruudust eraldab parabool y = x2. Selleks jagas ta lõigu [0; b] võrdseteks osadeks.
Ta vaatles ristkülikuid, mille ülemine parempoolne tipp puudutas parabooli (joonisel rohelised ristkülikud), nende ristkülikute summat nimetatakse otsitava pindala S alampiiriks.
Sulle võivad huvi pakkuda need õppematerjalid:
Liitmine 10 piires
Geomeetria
xy-koordinaatsüsteem
Lahutamine 20 piires
Kirjalik liitmine
Protsendi rakendused igapäevaelus
Väike protsendiamps
Tasandilised kujundid
Kirjalik lahutamine
Peastarvutamine I kooliastmele
Hariliku murru kordamine
Ruutvõrrandi abil lahenduvad tekstülesanded
Kirjeldav statistika
NUPUTAME KOOS! Tasapinnalised kujundid
Ruutvõrrand
Peastarvutamine eelkoolile
Üksliikmed, hulkliikmed ja tehted nendega
Ruutvõrrandi mõiste, ruutvõrrandi lahendivalem, ruutvõrrandi liigid
Ratsionaalavaldised
Numbrilised seosed
Selliste ristkülikute, mille ülemine parempoolne tipp puudutab parabooli (joonisel kollased ristkülikud), summat nimetatakse otsitava pindala S ülempiiriks. Mida suuremaks arvuks osadeks me vaadeldava lõigu jaotame, seda enam lähenevad ülem- ja alampiir otstitavale summale.
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!