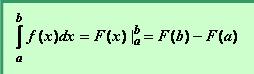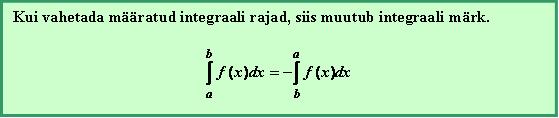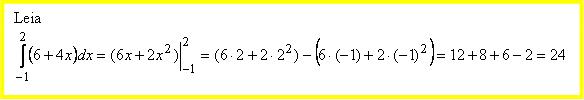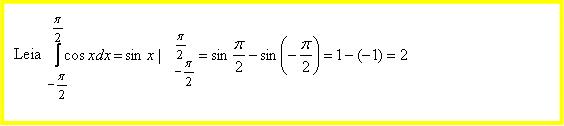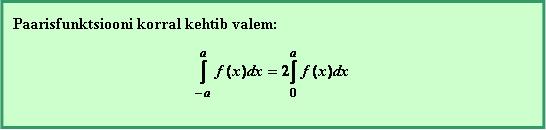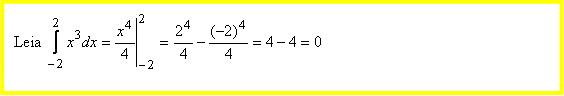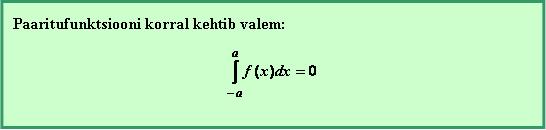Kui funktsioon f(x) on integreeruv lõigus [a;b], siis tema kõigi algfunktsioonide muudud, mis vastavad argumendi muudule 
=b – a, on võrdsed.
Seda on kerge mõista geomeetrilise esituse kaudu. Et algfunktsioonid erinevad vaid konstantse liidetava poolest, siis nende graafikud on saadavad üksteisest y-telje sihilise lükkega. Vastavad muudud on võrdsed.
Järgneval GeoGebra lehel, saad muuta konstanti C ja veenduda selles, et funktsiooni muudud on võrdsed.
Definitsioon
Arve a ja b nimetatakse vastavalt integraali alumiseks ja ülemiseks rajaks. Olgu F(x) funktsiooni f(x) mingi algfunktsioon, s.t. F´(x) = f(x) lõigus [a; b], siis määratud integraali defineerib valem:
Seda valemit nimetatakse ka Newton-Leibnizi valemiks.
Ka määratud integraali leidmise tehet nimetatakse integreerimiseks, sest siingi tuleb esmalt leida antud funktsiooni algfunktsioon.
Samuti on määratud integraalil analoogilised omadused nagu määramata integraalil, kuid lisanduvad ka mõned uued omadused.
Omadused
1. Konstandiga korrutatud funktsiooni integreerimine:
2. Summa või vahe integreerimine:
3. Integraali rajade vahetamine:
4. Määratud integraali aditiivsus:
Näited:
Arutelu
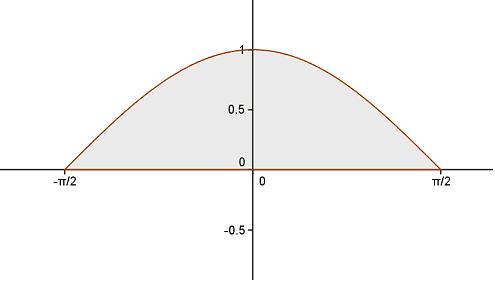
Tee joonis ja mõtle, kas seda oleks võimalik leida ka teisiti.
Tegemist paarisfunktsiooniga. Paarisfunktsiooni graafik on sümmeetriline y-telje suhtes. Kui ka rajad on sümmeetrilised y-telje suhtes, siis kehtib valem:
Arutelu
Tee joonis ja mõtle, kas seda oleks võimalik leida ka teisit
