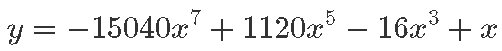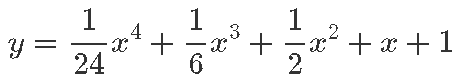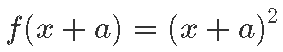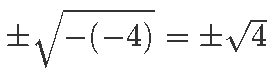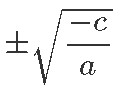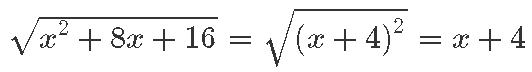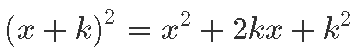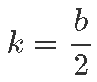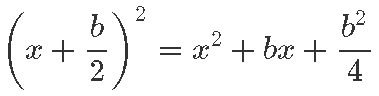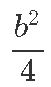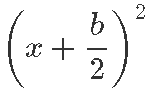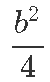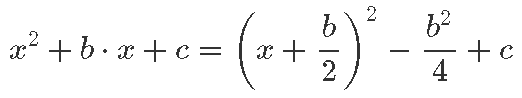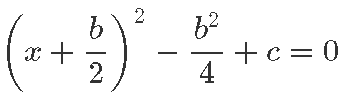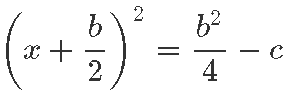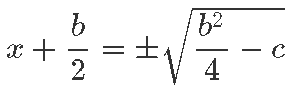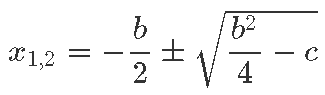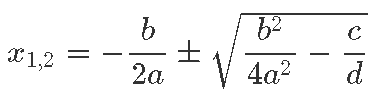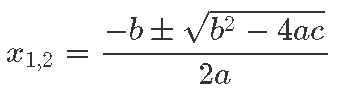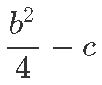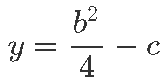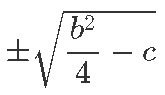Polünoom
Polünoom on üks keeruline võõrsõna, aga sellel ei maksa end heidutada lasta – hullemategi sõnade taga peitub vahel täiesti toredaid selle: näiteks trubaduur või seismoloog. Polünoomide korral on tegemist vaid teatud lihtsate ja hästi uuritud funktsioonidega.
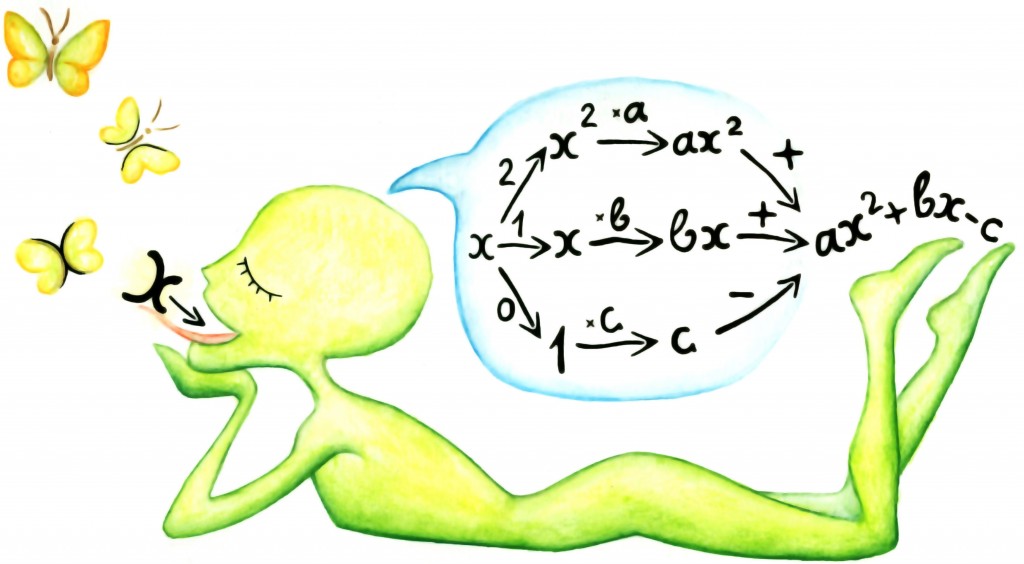
Üks polünoom oskab sisendarvudega teha ainult väga tavalisi tehteid: ta võib neid võtta erinevatesse naturaalarvulistesse astmetesse, neid mingi arvuga (kordajaga) läbi korrutada ning siis saadud tulemusi liita ja lahutada. Seega vägagi sõbralik sell.
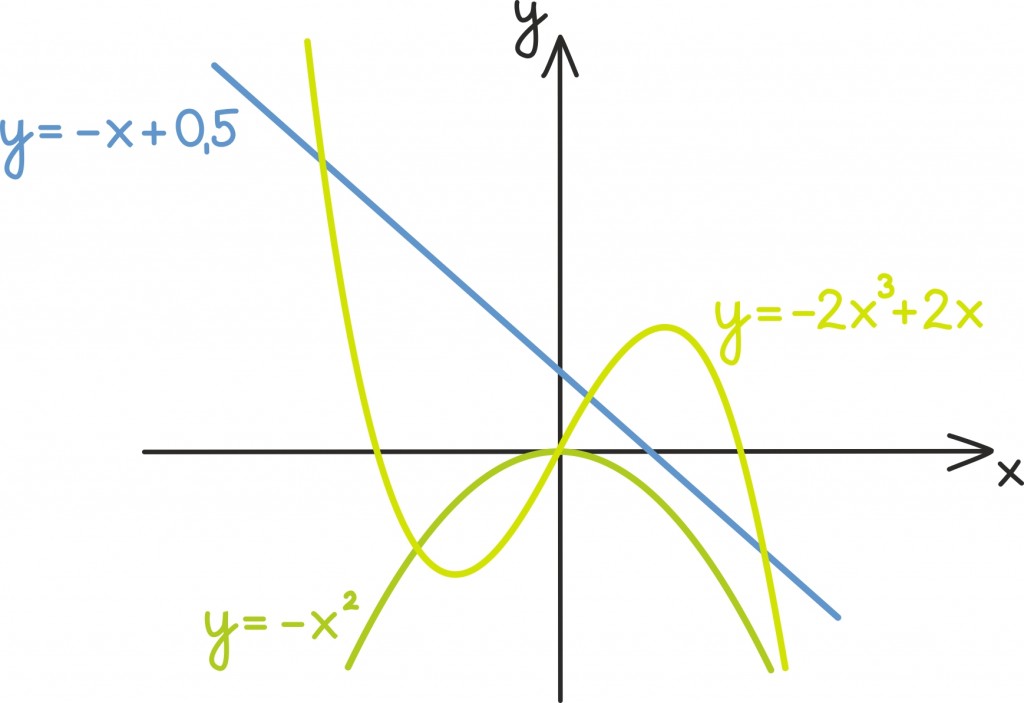
Kui räägitakse reaalarvulistest polünoomidest, siis on nii sisendarvud, kordajad kui ka saadav väljund reaalarvud. Näiteks kõik järgmised funktsioonid on reaalarvulised polünoomid:
Nagu majaga katus, nii käib polünoomiga alati kaasas tema aste. Siin peetakse lihtsalt silmas kõige kõrgema astmega liikme astet. Näiteks esimene toodud polünoomidest on teise astme polünoom ehk ruutfunktsioon, teine on esimese astme polünoom ehk lineaarne funktsioon ning kolmas viienda astme polünoom.
Omadused
Kas Sa usud, et kui liidad või korrutad omavahel kaks polünoomi, siis on tulemuseks jällegi üks polünoom?
See omadus on hea ja kasulik sellepärast, et nüüd võime alati julgelt polünoome kokku liita, lahutada ja korrutada, ilma et peaksime kartma, et meid ootab ees mingisugune hirmus funktsioon, mille arvutamine võiks meil üle jõu käia.
Teiseks heaks omaduseks on polünoomide sile ja mõnus graafik – nende graafiku saab tõmmata joonisele ühe joonega ehk nad on pidevad. Pidevuse kirjeldusest ja tähtsusest loe pidevuse peatükist [lk 317].
Kolmandaks on polünoomid sõbralikud ka kahe reaalfunktsioonidega ette võetava teisenduse suhtes. Esimest teisendust nimetatakse tuletiseks – sisuliselt näitab tuletis funktsiooni muutumise kiirust [lk 320]. Teist nimetatakse integraaliks ning see iseloomustab näiteks funktsiooni graafiku ja -telje vahele jäävat pindala [lk 340]. Tuleb välja, et polünoomidega neidsamu teisendusi tehes saame vastu jälle polünoomid.
- Polünoomi tuletis on ühe võrra väiksema astmega polünoom.
- Polünoomi määramata integraal on ühe võrra kõrgema astmega polünoom.
Polünoomide pere on üsna kinnine – pea kõik tähtis, mis nendega teha võib, annab tulemuseks taas polünoomi.
Sulle võivad huvi pakkuda need õppematerjalid:
Liitmine ja lahutamine 10 piires
Lahutamine 20 piires
Funktsioonide graafikud
Kirjalik lahutamine
II kooliastme matemaatika reeglite kordamine
Ruutvõrrandi mõiste, ruutvõrrandi lahendivalem, ruutvõrrandi liigid
Funktsioonid ja nende graafikud
Hariliku murru kordamine
Ruutvõrrand
Kell ja kellaaeg
Algebralised murrud
Funktsioonide graafikute lõikepunktide leidmine
Ruutvõrrandi abil lahenduvad tekstülesanded
Peastarvutamine eelkoolile
Liitmine ja lahutamine 20 piires
Ruutjuur, tehted ruutjuurtega
Ruumilised kujundid
Liitmine 10 piires
8. klassi matemaatika teooriavideod
xy-koordinaatsüsteem
Miks osutuvad polünoomid nõnda oluliseks?
Polünoomid on tänu piiratud operatsioonidele üsna lihtsad – neid on lihtne kirjeldada, nendega on lihtne ringi käia, nende väärtusi on lihtne leida nii inimesel kui ka arvutil.
Samas on nad kõigest sellest lihtsusest hoolimata uskumatult laia haardega tegelased: ükskõik millise teise vähegi mõistliku (näiteks pideva) funktsiooni jaoks leidub alati polünoom, mis näeb temaga nii sarnane välja, et isegi luubiga vaadates võiks nad omavahel sassi ajada.
Näiteks polünoom
näeb piirkonnas –π kuni π välja täpselt nagu siinusfunktsioon [lk 214]:
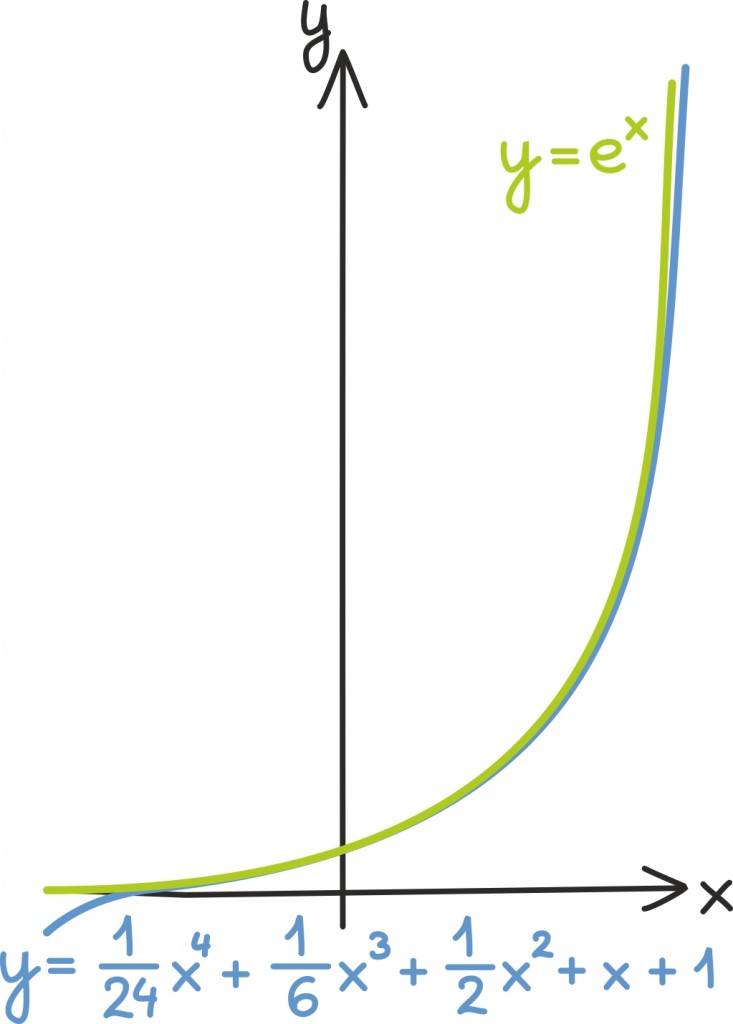
ning polünoom
kirjeldab nulli lähedal hästi eksponentsiaalfunktsiooni y = ex.
See, et võime teisi funktsioone nii kergelt polünoomidega segamini ajada, tähendab, et nii mõnigi kord võimegi reaalses elus ning arvutustes käsitleda ainult polünoomfunktsioone – oskame nendega hästi ringi käia ning samas annavad nad meile piisavalt head informatsiooni päriselt toimuva kohta.
Võime lugeja meelehärmiks avaldada lausa ühe saladuse: isegi kui käsite oma taskuarvutil logaritmi võtta, arvutab too kaabakas ainult polünoome – ta jäljendab õiget funktsiooni aga nii kavalalt ja tublilt, et sellest ei olegi võimalik taskuarvuti täpsuse juures aru saada. Arvutid kasutavadki kõikide enda arvutuste jaoks ainult polünoome.
Nullkohad ja mugavale kujule tegurdamine
Oluliseks märksõnaks on polünoomide puhul nende nullkohad: sisendarvud, mille korral polünoomi väärtus on null.
Selgub, et nende abil on võimalik esitada polünoomi väga mugaval kujul: kui teame, et polünoomi P(x) nullkohad on r1, r2, …, rn, võime P kirjutada kujul
kus c on lihtsalt üks reaalarv.
Näiteks ruutfunktsiooni korral saame
mis ongi kogu see tegurdamise (ja igasuguse teisendamise) lõbu, mida koolipingis hoolega õpitakse: funktsioonide esitamine mugavamas kujus.
Võib tekkida küsimus, miks peaksid meid huvitama just nullkohad ja mitte näiteks „kolmkohad” – kohad, kus polünoomi väärtus on kolm. Õigupoolest on vastus õige lihtne: nulli korral on tekkiv kuju lihtsalt kõige kompaktsem ning nullkohad jäävad paika ka funktsiooni läbikorrutamisel mõne reaalarvuga.
Lisaks kui oskame leida nullkohti, siis kolmkohtade leidmiseks tuleb polünoomist lahutada kolm ning leida saadud tulemuse nullkohad.
Saame näidata, et kui polünoomi aste on n, siis tal ei saa olla rohkem kui n nullkohta (või „kolmkohta”). Sellest tulemusest võib intuitiivselt aru saada, kui mõelda, et lineaarfunktsioon ei tee ühtegi jõnksu, ruutfunktsioon teeb maksimaalselt ühe jõnksu, kuupfunktsioon kaks jõnksu ja analoogselt teeb nastme polünoom n – 1 jõnksu. Et pärast teatud nullkohta polünoomiga jälle nulli tagasi jõuda, on meil alati tarvis ühte jõnksu ja n – 1 jõnksu abil võime nõnda nulli jõuda täpselt n korda.
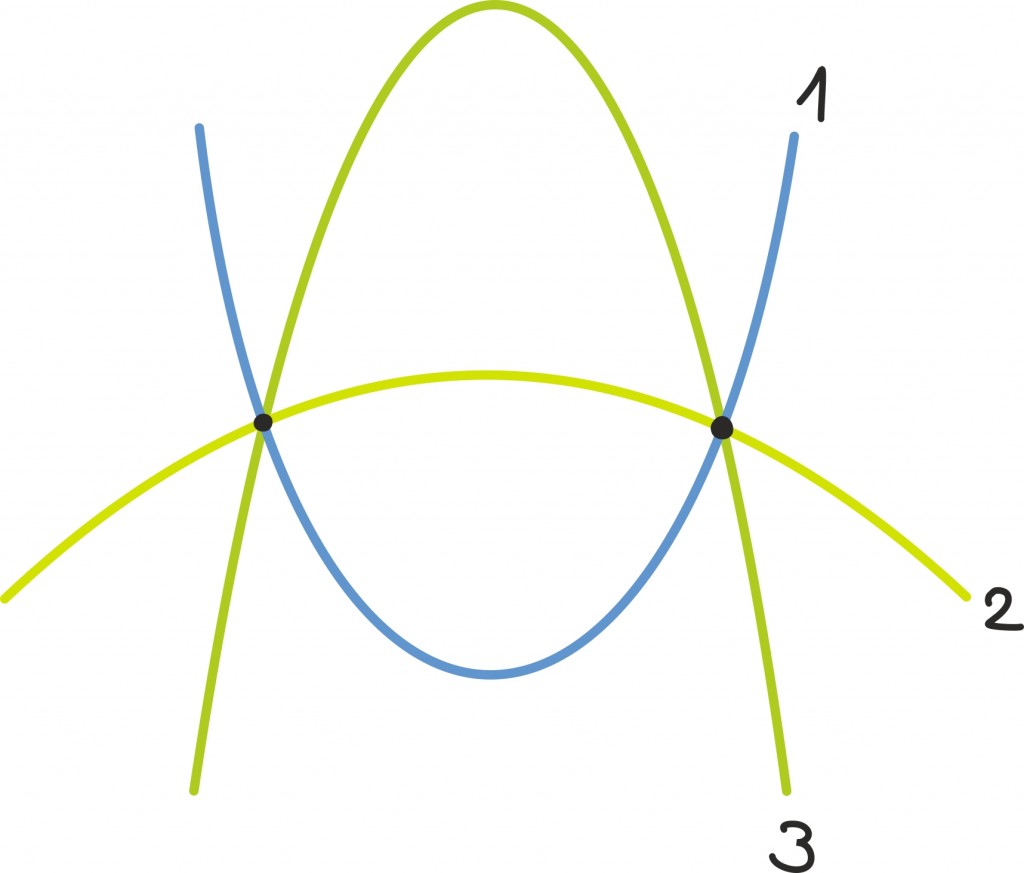
Kõigest sellest võib kavalam järeldada, et kui kaks n -astme polünoomi on võrdsed n + 1 punktis, siis on nad võrdsed absoluutselt igal pool (tõestuseks tuleb lihtsalt uurida nende kahe polünoomi lahutamisel saadavat polünoomi). Sellel üllataval teadmisel on rakendused ka päriselus.
Kuidas peita kolmekesi ühist varandust?
Oletame, et leiate sõpradega seiklusmatkalt kena koguse briljante ja otsustate peita kogu saagi viieks aastaks seifi. Eks ikka selleks, et enne hästi järele mõelda, mis kogu varaga pihta hakata.
Teil on olemas ka 9-märgilise salakoodiga ultramodernne seif, kuhu briljandid varjule panna. Kuidas aga kindlaks teha, et te ainult kolmekesi üheskoos saaksite seifi avada? Toredaks abimeheks osutub siin polünoomide tundmine, eriti üks märkus lisateadmistest – iga n-kohalise polünoomi määravad üheselt ära temal asetsevat n + 1 punkti.
Seega, kui näiteks on antud ruutpolünoom x2 + ax +b, siis niipea kui teame kolme temal asetsevat punkti, teame tegelikult kõiki polünoomil asetsevaid punkte. Kuid suvalise kahe punkti teadmine ei ütle polünoomi kohta just väga palju.
Idee on nüüd selge: lasete arvutil välja mõelda mõne suvalise polünoomi ning igaühele väljastada täpselt ühe punkti sealt polünoomilt. Salakoodiks saab olema kokkukirjutatult selle polünoomi väärtus kohtadel –1, 0 ja 2.
siis osutub salakoodiks 345308240, sest näiteks funktsiooni väärtus kohal –1 on –12 – 36 · (–1) + 308 = 345 jne.
Kui sõber Mart saab punkti (1; 273), sõber Ants punkti (20; –12) ning ise saad punkti (9; 65), siis nagu graafikult näete, pole Mardil ja Antsul kahekesi õigeks vastuseks suurt lootust: neil ei olekski õigupoolest põhjust ühtegi kombinatsiooni väga eelistada, sest kaks punkti ei ütle võimaliku polünoomi kohta peaaegu mitte midagi.
Tähelepanelik lugeja võiks vaielda, et miks ei võiks seda olukorda lahendada tunduvalt lihtsamalt: andes igale sõbrale lihtsalt kolm salakoodi numbrit. See on tõesti võimalik, kuid siis peaks kood olema tunduvalt pikem, sest vastasel korral võivad kaks sõpra kokku tulla ning kolmanda sõbra puuduvad numbrid lihtsalt läbi proovida, mis eelneva lahenduse puhul poleks võimalik.
Ruutfunktsioon ja tema lahendi valem
Ruutfunktsioon või teisisõnu ruutpolünoom on ilmselt koolitunni populaarseim ning käsitletuim funktsioon.
Seda populaarsust saab ka natuke selgitada: ta on väga levinud (mäletate ehk füüsikast läbitud distantsi avaldamist kiirenduse kaudu?), teda on piisavalt lihtne joonistada ning kirja panna ja samas on ruutfunktsiooni nullkohtadel esmapilgul keerulisena näiv lahendivalem, millega õpilasi hirmutada. Või siiski?
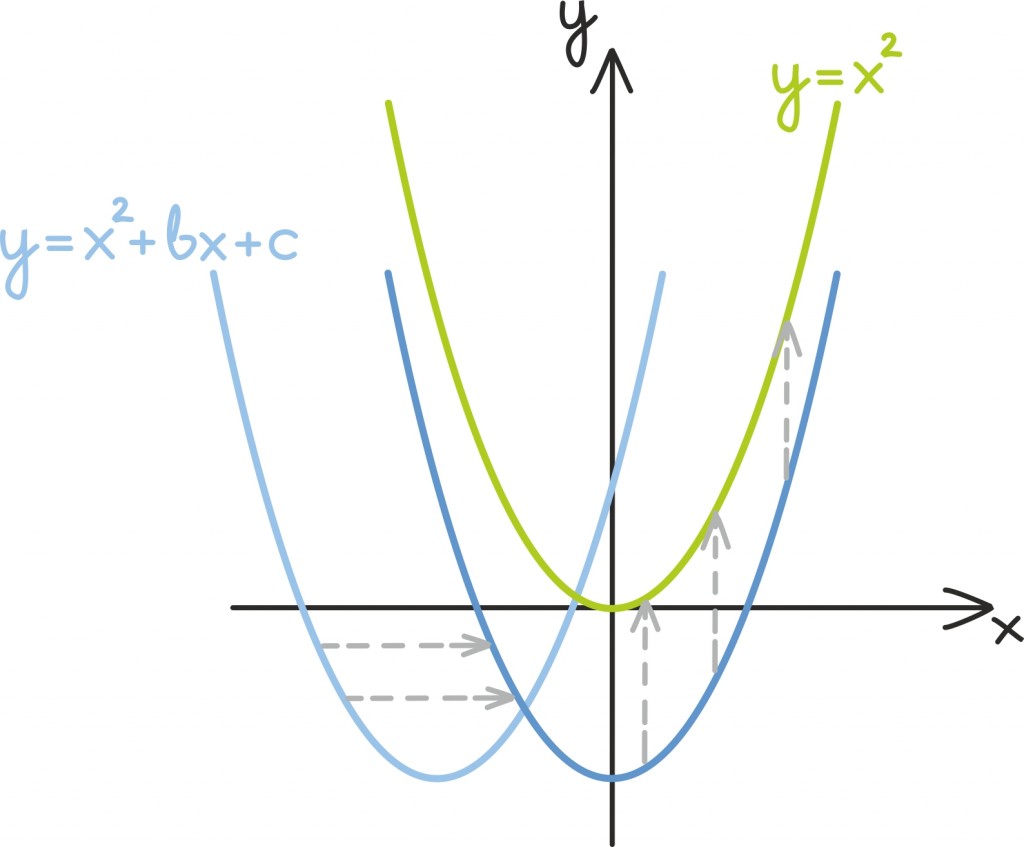
Alustame ruutfunktsiooniga tutvumist tema graafiku juurest ja näitame, kuidas kõik erinevad ruutfunktsioonid on lihtsate geomeetriliste teisenduste kaudu omavahel seotud. Seejärel leiame ruutfunktsiooni lahendivalemi ja anname sellelegi geomeetrilise intuitsiooni.
Ruutfunktsiooni graafik
Niipea kui oleme joonistanud ühe funktsiooni graafiku, saame hakata sellega mängima. Näiteks võime seda graafikut nihutada ja erinevatest sirgetest peegeldada.
Kuigi lõbus on see alati, saab sellest protseduurist ka mõnikord kasu lõigata. Näiteks saame nende teisenduste abil meeles pidada trigonomeetriliste teisenduste valemeid [lk 242]. Ruutfunktsiooni korral võime selliste geomeetriliste teisenduste teel luua ühest algfunktsioonist pea kõik teised ruutfunktsioonid ning, nagu hiljem näeme, leida isegi ruutvõrrandi lahendivalemi.
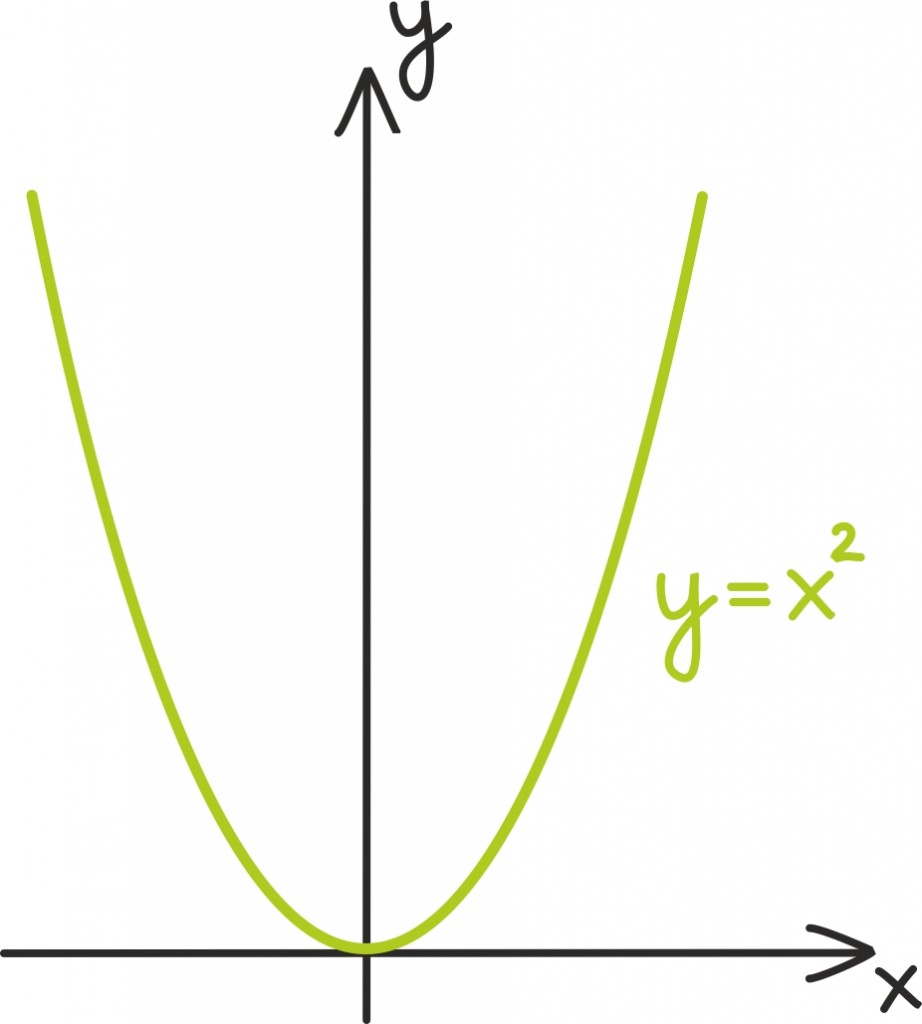
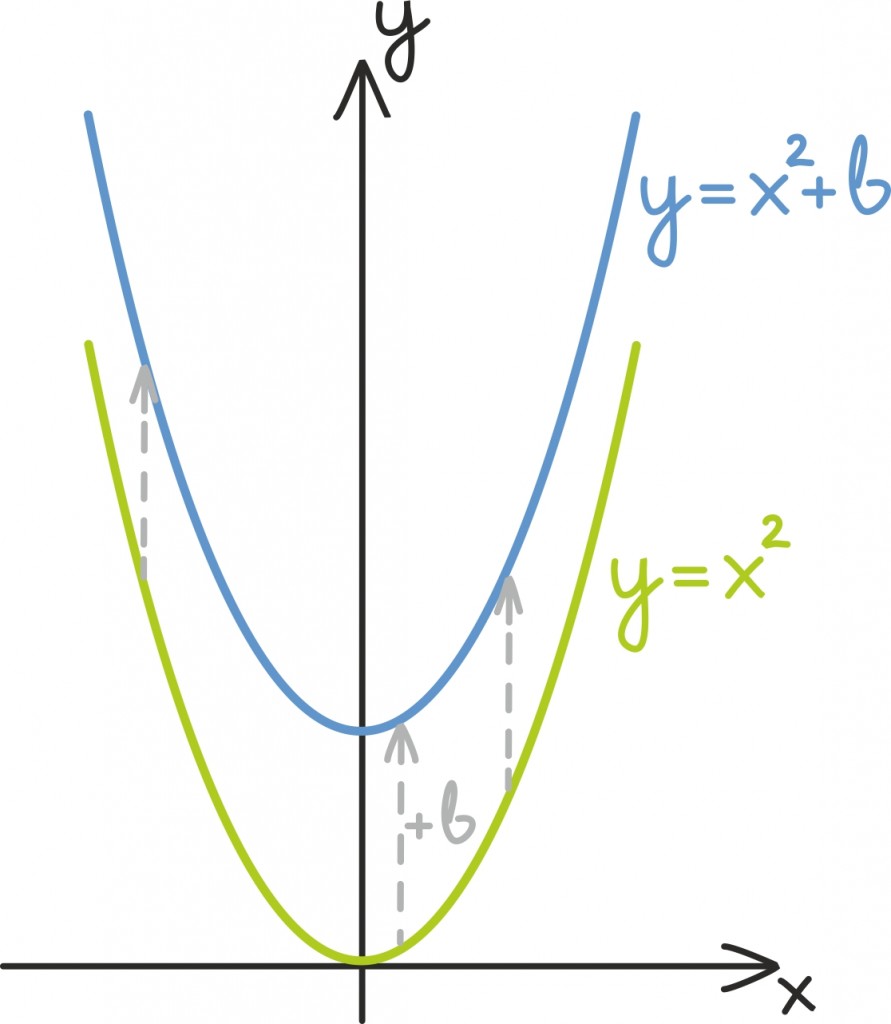
Alustame ruutfunktsioonist
Teda üles-alla nihutades saame funktsioonide kujus
graafikud.
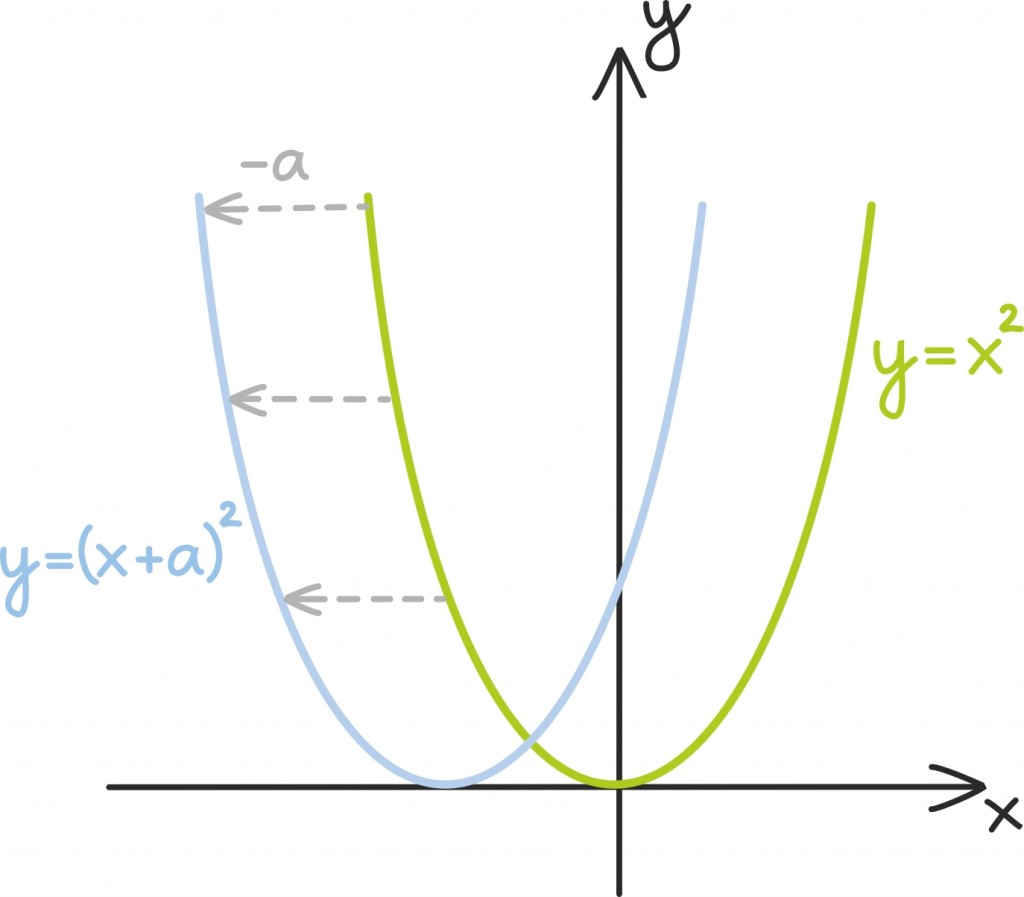
Nihutades algset funktsiooni aga horisontaalselt – või teisisõnu nihutades x-telge tema suhtes –, saame kõik funktsioonid kujus
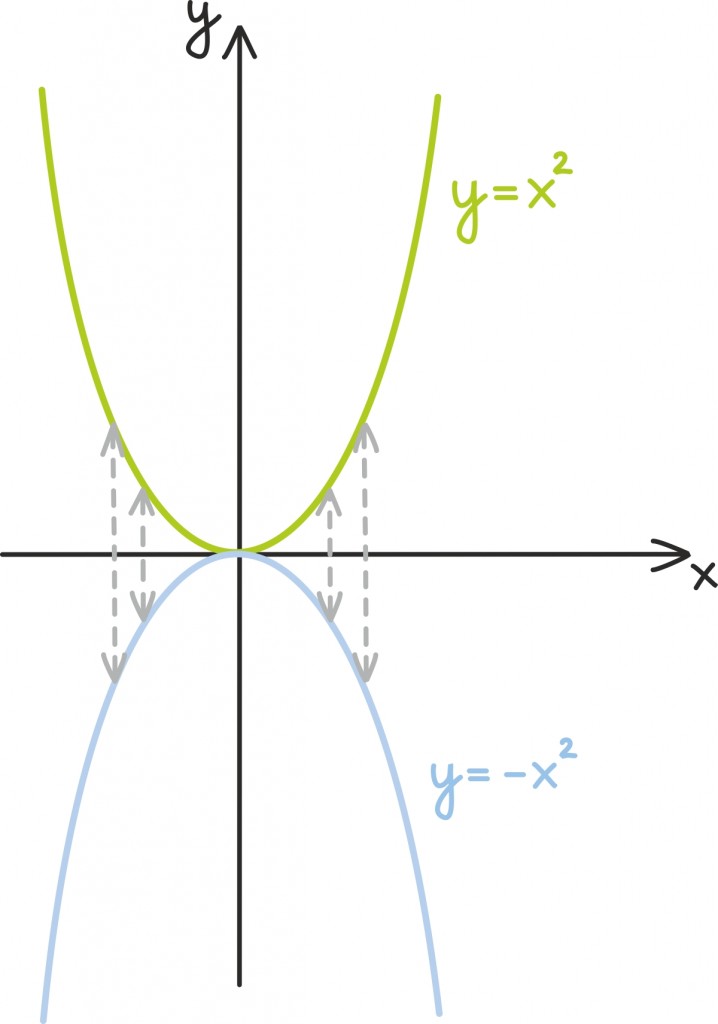
Nüüd, kui peegeldame esialgset funktsiooni x-telje suhtes, saame funktsiooni
graafiku.
Algse funktsiooni peegeldus y-telje suhtes ei tee aga midagi huvitavat – meie funktsioon on y-telje suhtes sümmeetriline ja jääb peegelduse tõttu samaks.
Kõiki neid teisendusi võib muidugi teha ka järjepanu ning nii neid kombineerides leiaksime kõikide funktsioonide kujus
graafikud. Kui tahaksime päris üldkujusse jõuda, peaksime lisaks veel lubama ka y-telje skaleerimist.
Varsti näeme, et selline geomeetriline mõtlemine annab aimu ka ruutfunktsiooni lahendivalemitagamaadest. Enne seda lahendame aga ruutvõrrandi puhtalt algebraliselt.
Ruutfunktsiooni lahendivalem
Ruutfunktsiooni lahendivalem võib jääda pisut müstiliseks, kuna tihti ei ole aega seda korralikult tuletada. Tegelikult ei ole selles lahendivalemis midagi hirmsat, kui on viitsimist pisut kaasa mõtelda. Lubame, et ei lähe kauem, kui korraliku suure koorejäätise söömine aega võtaks, ning lubame jäätise ka seltsi võtta. Üritame siis valemi samm-sammult tuletada.
Kõige lihtsam võrrand, mis võib ette tulla, on muidugix2 + c = 0 ehk x2 = –c. Sel juhul – kuna ruutjuurt [lk 111] oskame ju hästi võtta – teame, et vastuseks on ±√–c. Oluline on märgata, et miinusmärk c ees ei tähenda sugugi, et meil peaks kohe tegemist olema negatiivse arvuga. Näiteks kui c = –4 saame võrrandix2 – 4 = 0 ning lahenditeks oleksid
ehk 2 ja –2.
Raskusi ei valmista ka võrrand a · x2 + c = 0, kuna sel juhul võime lihtsalt kogu võrrandi jagada a-ga läbi ning jõuame sarnaselt eelnevaga vastuseni
Mis aga juhtub, kui juurde tuleb liige b · x ehk kui ruutvõrrand on kujus x2 + bx + c = 0? Tuletame meelde, et võrrandi lahendamine tähendab endiselt, et leiame vastuse kujul
Üldkujus on aga sees ka x-i ruut. Eelnevalt saime temast lahti, rakendades ruutjuurt, ja ausalt öelda, ega mingit muud müstilist trikki ruudust lahti saamiseks pole. Seega tahame ka seekord võtta ruutjuurt. Aga millest?
Ruutjuurt oskame võtta hästi ainult ruutavaldistest. Esimesel juhul oli meil lihtne ruutavaldis x2, seekord jõlgub kaasa aga ka libe bx-liige. Kuidas temast lahti saada?
Tuleb lihtsalt märgata, et tegelikult oskame me võtta ruutjuurt mitte ainult x2-st, vaid ka näiteks (x + 4)2-st või (x –1)2-st.
See on abiks, kuna (x + 4)2 = x2 + 8x + 16 annab meile ka x-iga liikme! Nii saame avaldisest x2 + 8x + 16 võtta ilusti ruutjuurt
Seega tuleb juurimise jaoks leida x-ile sulgudesse õige kaaslane, mis lahtikorrutades annaks liikme bx.
Tuletame meelde, et ruutliikme tegurdamine käib järgnevalt:
Kui nüüd valime
ongi liikme x ees soovitud kordaja b
See näeb välja juba peaaegu nagu meie algne võrrand x2 + b · x + c = 0.
Ainsa vahena on ülemises valemis lihtsalt üks üleliigne liige
ning liige c on hoopis puudu.
Seega peame algse ruutfunktsiooni kirjeldamiseks lihtsalt ruudust
maha lahutama üleliigse osa
ja tagasi liitma c:
Nii saab meie võrrand x2 + b · x + c = 0 kuju
Viies osa liikmeid teisele poole, oleme juba väga heas positsioonis juurimiseks:
Siin saame võtta ruutjuure ning vastuseks tuleb
ehk
Taandatud ruutvõrrandi lahendivalem ongi käes!
Kui x2 ees on veel kordaja a, peame lihtsalt b ja c läbi jagama a-ga ning jõuame just läbi arutatud olukorrani. Nii on ruutvõrrandi üldkuju ax +bx + x = 0 lahendivalemiks
mida tihti kirjutatakse ka kujus
Kontrolli, et ka viimane teisendus kehtib!
Selle valemi abil võib lahendada ükskõik millist ruutvõrrandit. Näiteks kui õpetaja lööb lauale ruutvõrrandi x2 – 3x – 10 = 0, võime välja võtta oma valemi, sinna sisse pookida a = 1, b = –3 ning c = –10 ning saamegi vastuseks lahendid –2 ja 5.
Lahendivalem geomeetriliselt
Lubasime, et lahendivalemi leidmisest saab ka geomeetriliselt mõelda. Kuna meil on tegelikult juba ruutvõrrandi lahendivalem leitud, siis mingis mõttes on see muidugi tühi töö. Siiski aitab järgnev mõttekäik anda ruutvõrrandi lahendivalemi leidmise erinevatele etappidele ja seega ka lahendivalemile endale geomeetrilist intuitsiooni ning seeläbi ehk aitab valemit ja selle tuletust meeles pidada.
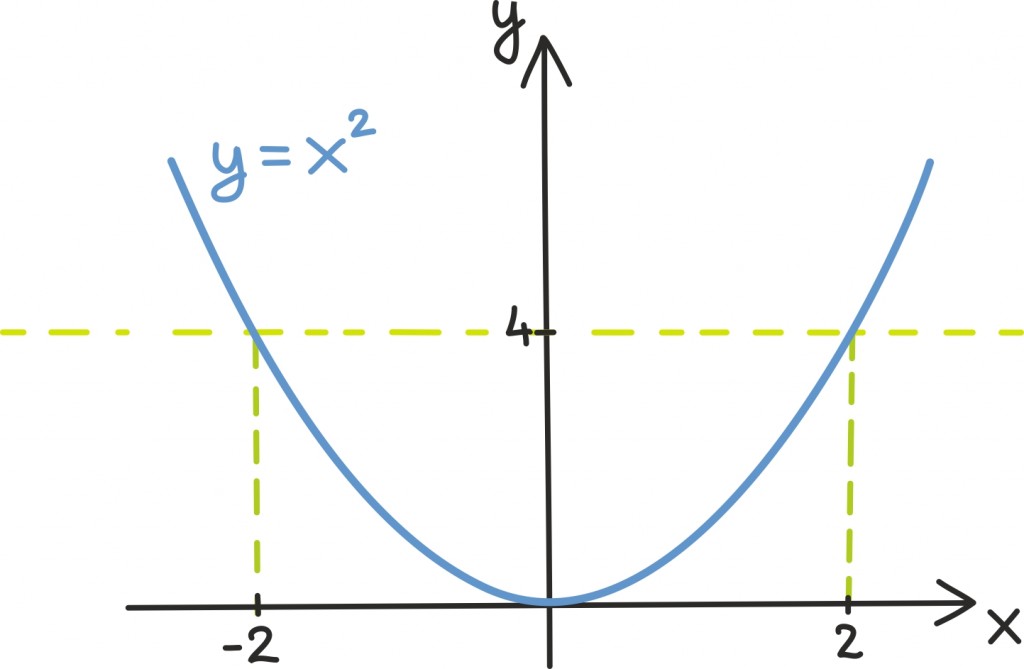
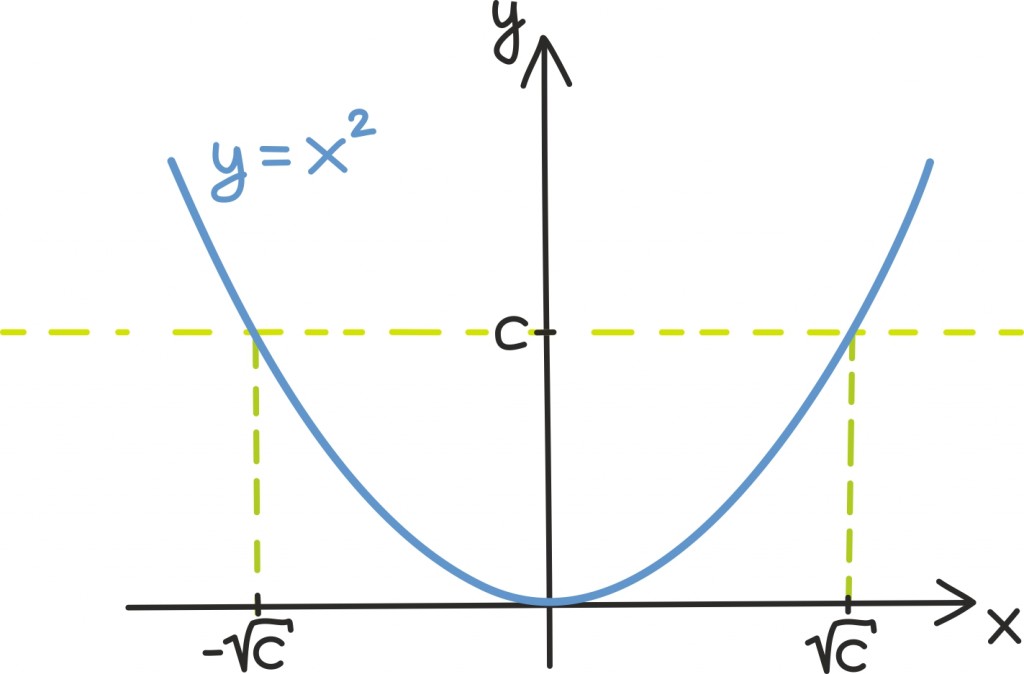
Aluspunktiks on tähelepanek, et ruutvõrrandi x2 = clahendamine tähendab geomeetriliselt täpselt funktsioonide y = x2 ning y = c graafikute lõikepunktide x-koordinaatide leidmist. Seda muidugi oskame teha ruutjuurt võttes ja vastuseks on
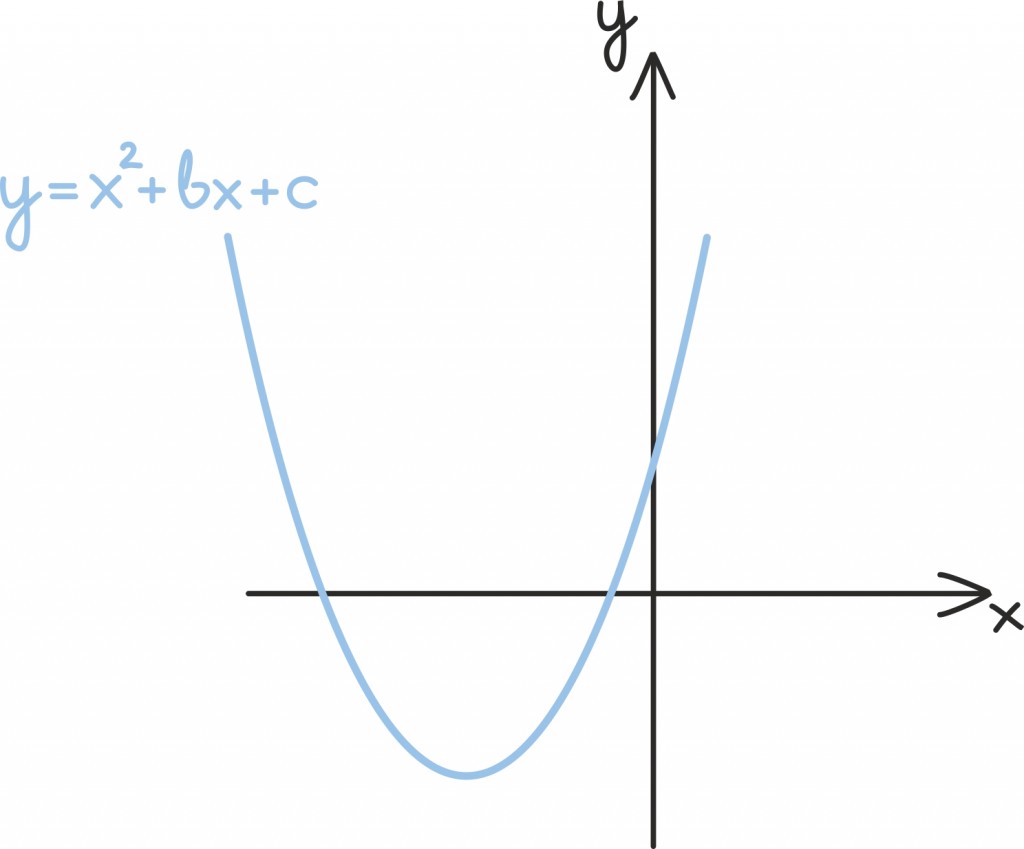
Peaaegu üldkujus ruutvõrrandi x2 + bx + c = 0 lahendamine tähendab omakorda muidugi ruutfunktsiooni y = x2 + bx + c ning x-telje lõikepunktide leidmist.
Kogu ruutfunktsiooni lahendivalemi leidmiseks vaja läinud teisendusterea eesmärk oli taandada teine olukord esimesele, taandada keerulisemate lõikepunktide leidmine lihtsamate lõikepunktide leidmisele. Mingis mõttes tähendab see, et tahame oma suvalise ruutfunktsiooni graafiku teisendada ruutfunktsiooni y = x2 graafikuks.
Selle jaoks nihutame esmalt funktsiooni graafikut
võrra horisontaalselt (positiivne suund on paremale), et funktsiooni graafik oleks sümmeetriline y-telje suhtes.
Seejärel liigutame graafikut
võrra vertikaalselt (positiivne suund on üles), et viia graafiku kõige alumine punkt täpselt koordinaatteljestiku nullpunkti.
Nii oleme kahe teisenduse abil jõudnud funktsiooni y= x2 graafikuni.
Kuidas on teisenenud algse ruutvõrrandi nullkohad? Kui enne olid nad sirge y = 0 ning algse ruutfunktsiooni lõikepunktid, siis teisenduste käigus esiteks nihutasime neid lõikepunkte
võrra horisontaalselt ning seejärel tõstsime
võrra.
Nende teisenduste järel said nullkohtadest funktsiooni y = x2 ning sirge
lõikepunktid.
Nende lõikepunktide x-koordinaadid on aga täpselt antud valemiga
Kuna vertikaalsed, üles-alla teisendused x-koordinaate ei muuda, peame ainult arvesse võtma veel horisontaalse nihke. Uued lõikepunktid on algsete suhtes
võrra nihutatud, seega peame algsete lõikepunktidex-koordinaatide leidmiseks lahutama veel
Saamegi taas kord loodetud vastuse.
Seekord on aga mõlemal liikmel ka taust: esimene tuleb funktsiooni sellisest üles-alla nihutamisest, et ta istuks täpselt horisontaalteljel. Teine pärineb horisontaalsest nihutamisest, mis viib funktsiooni graafiku sümmeetriliseks vertikaaltelje suhtes.