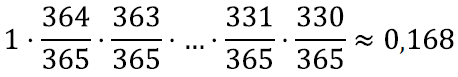Tõenäosus ja intuitsioon
Monty Halli probleem
Oletame, et oled telemängus ning pead valima kolme ukse vahel. Ühe ukse taga on soliidne sportauto, ülejäänud kahe ukse taga seisab aga kurvameelne kits. Kuna kõik uksed on täpselt ühesugused, valid ilmselt alustuseks ühe neist ustest üsna suvaliselt. Enne veel, kui kõike teadev mängujuht Monty Hall selle ukse lahti teeb, avab ta kahest allesjäänud uksest veel ühe ukse. Kusjuures ta avab just sellise, mille taga peidab end kurvameelne kits. Nüüd pakub mängujuht Sulle valiku: kas Sa sooviksid muuta oma ukse valikut?
Loomulik küsimus on: kas oleks kasulik see vahetus teha?
Esimene reaktsioon võiks olla, et kui pärast on kaks ust alles, siis ei ole vahet, kas vahetada või mitte – on ju ühe avamata ukse taga kits ja teise taga auto ning seega auto võitmise tõenäosus täpselt pool. Sellist esmast intuitsiooni jagavad paljud, sealjuures ka uhkete doktorikraadidega matemaatikud ja teadlased.
Sulle võivad huvi pakkuda need õppematerjalid:
Liitmine ja lahutamine 10 piires
Lahutamine 20 piires
Funktsioonide graafikud
Kirjalik lahutamine
II kooliastme matemaatika reeglite kordamine
Ruutvõrrandi mõiste, ruutvõrrandi lahendivalem, ruutvõrrandi liigid
Funktsioonid ja nende graafikud
Hariliku murru kordamine
Ruutvõrrand
Kell ja kellaaeg
Algebralised murrud
Funktsioonide graafikute lõikepunktide leidmine
Ruutvõrrandi abil lahenduvad tekstülesanded
Peastarvutamine eelkoolile
Liitmine ja lahutamine 20 piires
Ruutjuur, tehted ruutjuurtega
Ruumilised kujundid
Liitmine 10 piires
8. klassi matemaatika teooriavideod
xy-koordinaatsüsteem
Simpsoni paradoks
Järgnevalt toome tõesti sündinud loo neerukivide vastaste ravimite katsetamisest. 1980-ndatel katsetati kahte erinevat ravimit, mõlemat eraldi väikeste neerukividega ja suurte neerukividega patsientidel.
Saadud tulemused võib koondada järgmisesse tabelisse, kus on toodud igas rühmas paranenud juhtumite protsent, sulgudes on veel lisaks kirjas täpselt, kui palju katsealuseid ühte või teise rühma kuulus.
Nagu näeme, näitavad esmapilgul tulemused, et nii väikeste kui suurte neerukivide korral toimib ravim A paremini. Kui jätta aga suurte ja väikeste kivide eristamine ära, näeksid kokku liidetud tulemused välja järgnevad:
Sünnipäeva ülesanne
Kui klassis on 36 õpilast, siis kui suur on tõenäosus, et kahel neist on sünnipäev samal päeval? Enne kui arvutusteni läheme, tee oma pakkumine!
Ja nüüd mõtle, mida see tõenäosus täpselt tähendab. Nagu oleme terves osas rõhutanud, viitab sõna tõenäosuse kasutamine kohe, et meil on mõttes mingi lihtsustatud kirjeldus. Lihtsustatud tähendab seda, et peame tegema ja teemegi mõned eeldused.
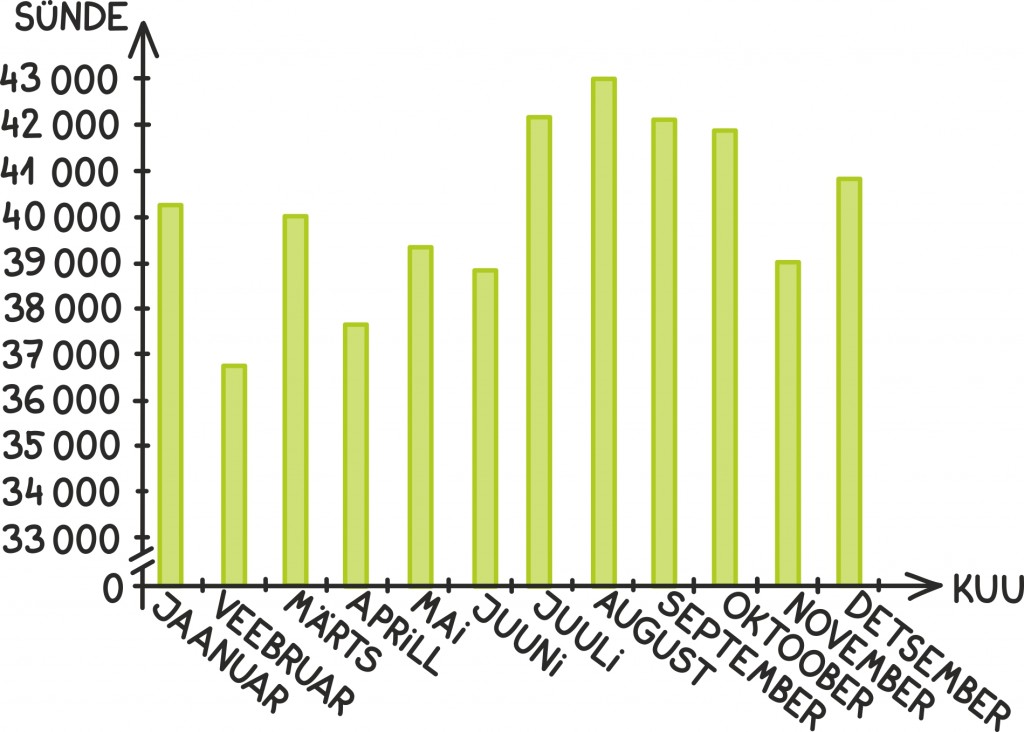
Näiteks seekord eeldame, et igal aasta päeval on sündimise tõenäosus võrdne. Kuigi tegelikult sünnib nädala sees rohkem lapsi kui nädalavahetusel ning kõik kuud ei ole aasta jooksul päris ühtlased, näeme ühe internetist leitud valimi graafikust, et tegemist on päris mõistliku eeldusega.
Teiseks, kui õpilaste hulgas pole just kaksikvendasid, võime eeldada julgelt, et kõikide õpilaste tõenäosus sündida ühel või teisel päeval on sõltumatu.
Seega võime mõelda, et veeretame lihtsalt 36 täringut, millel igal on 365 võrdväärset külge. Meie küsimus, mis tõenäosusega on kahel õpilasel samal päeval sünnipäev, on siis tõlgendatav kui küsimus, mis tõenäosusega jääb kahel täringul peale sama külg 365-st küljest.
Lihtsam on leida selle sündmuse vastandsündmuse tõenäosus: tõenäosus, et kõik täringud annavad erineva tulemuse.
Selle tarvis hakkame järjepanu arvutama. Kui meil on ainult täring, siis ta annab kindlasti eelnevatest erineva tulemuse. Kui nüüd veeretada järgminetäring, siis tõenäosus, et tulemus tuleb erinev, on
Kui võtta ette kolmas täring, siis juhul, kui esimeste täringute tulemused on erinevad, on tõenäosus, et tema silmade arv erineb mõlemast
Nii võime jätkata kuni 36 täringuni välja ning leida tõenäosuse, et kõik täringud andsid erineva tulemuse
Seega on vastandsündmuse tõenäosus, selle, et vähemalt kaks täringut 36-st andsid sama tulemuse, tervelt 1 – 0,168 = 0,832. Teisisõnu, selle kirjelduse ning nende eelduste põhjal on tõenäosus, et ühes 36 õpilasega klassis on kahel inimesel samal päeval sünnipäev, rohkem kui 0,8 ehk rohkem kui 80%! See on ikka päris kõrge!
Sama kirjeldust kasutades võib ka näidata, et juba 23 õpilasega klassis on tõenäosus, et kahel õpilasel juhtub sünnipäev täpselt samale päevale, rohkem kui pool. Kuidas on lugu Sinu klassis? Kui see tulemus üllatav tundub, siis ürita välja mõelda, miks see ikkagi üllatav tundub!