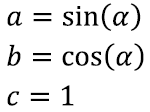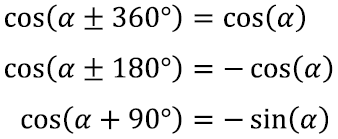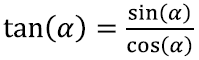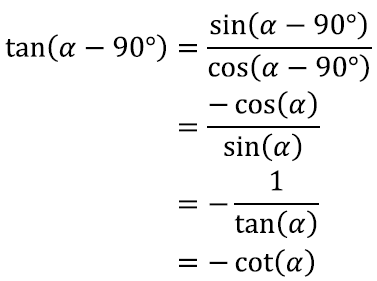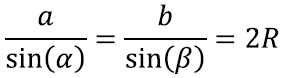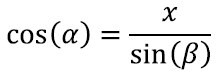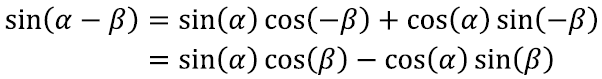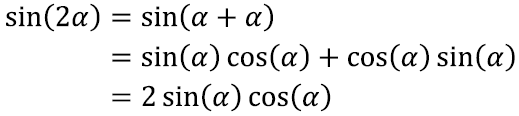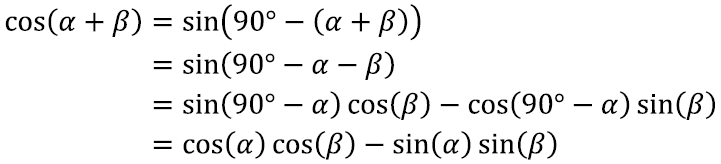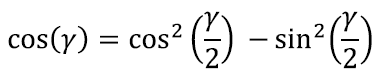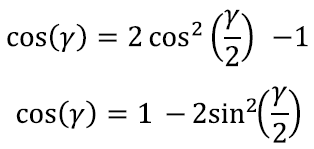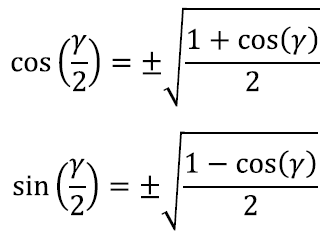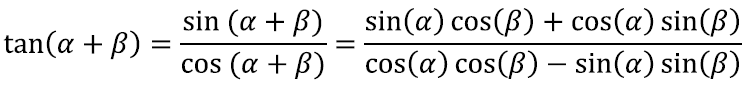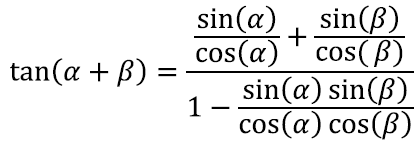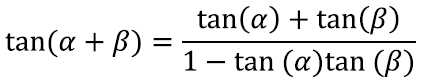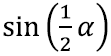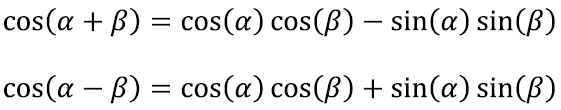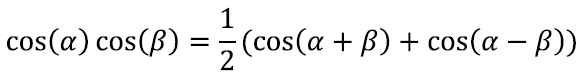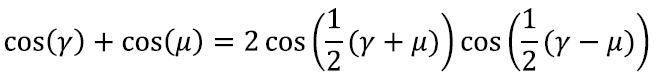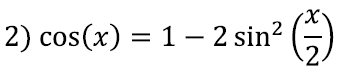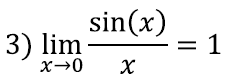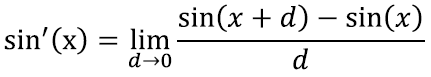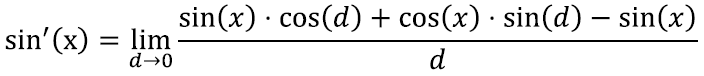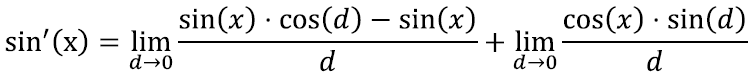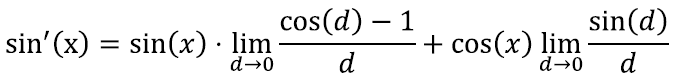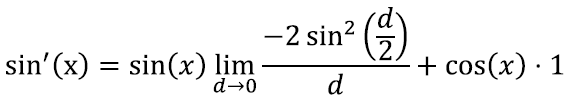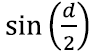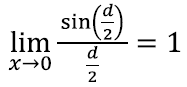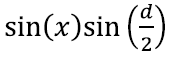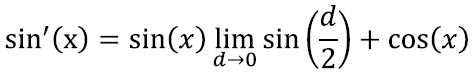Trigonomeetrilised avaldised ja nende teisendamine
Üks koolimatemaatikas enim tuska põhjustavaid teemasid on ilmselt trigonomeetriliste valemite teisendamine ja lihtsustamine.
Antakse ette mingi järjestus sümboleid ja kästakse sellest teha natuke lühem järjestus sümboleid. Selle jaoks, et teisendusi läbi viia, tuleb kasutada käputäit valemeid, mis näevad kõik välja täpselt ühesugused, aga mille hulgast iga kord vaid üks viib kiirelt sihile!
Nii jääbki tunne, et teha tuleb mingit maagiat ja on üsna selgusetu, mis kogu selle vaeva ja maagia mõte on.
Trigonomeetriliste funktsioonide vahelised seosed
Trigonomeetriliste funktsioonidega on seotud väga mitmeid erinevaid valemeid ja teisendusi. Võibolla kõige tuntumad ja lihtsamad neist pärinevad juba siinuse ja koosinuse definitsioonist täisnurkse kolmnurga kaudu. Nendest alustamegi. Seejärel käsitleme valemeid, mis on seotud trigonomeetriliste funktsioonide graafikute ilusate omadustega. Viimaks leiame valemeid, mis aitavad leida erinevaid summa- ja vahevalemeid.
Sulle võivad huvi pakkuda need õppematerjalid:
Liitmine ja lahutamine 10 piires
Ruutjuur, tehted ruutjuurtega
8. klassi matemaatika teooriavideod
Algebralised murrud
Protsendid põhikooli matemaatikas
Tasandilised kujundid
Ruumilised kujundid
NUPUTAME KOOS! Tasapinnalised kujundid
Üksliikmed, hulkliikmed ja tehted nendega
Valik harjutusülesandeid matemaatika riigieksamiks
Numbrilised seosed
Kell ja kellaaeg
Geomeetria
II kooliastme matemaatika reeglite kordamine
Väike algebraamps
Lahutamine 20 piires
Funktsioonide graafikud
Kirjeldav statistika
Ruutvõrrandi mõiste, ruutvõrrandi lahendivalem, ruutvõrrandi liigid
Liitmine ja lahutamine 20 piires
Seosed täisnurksest kolmnurgast
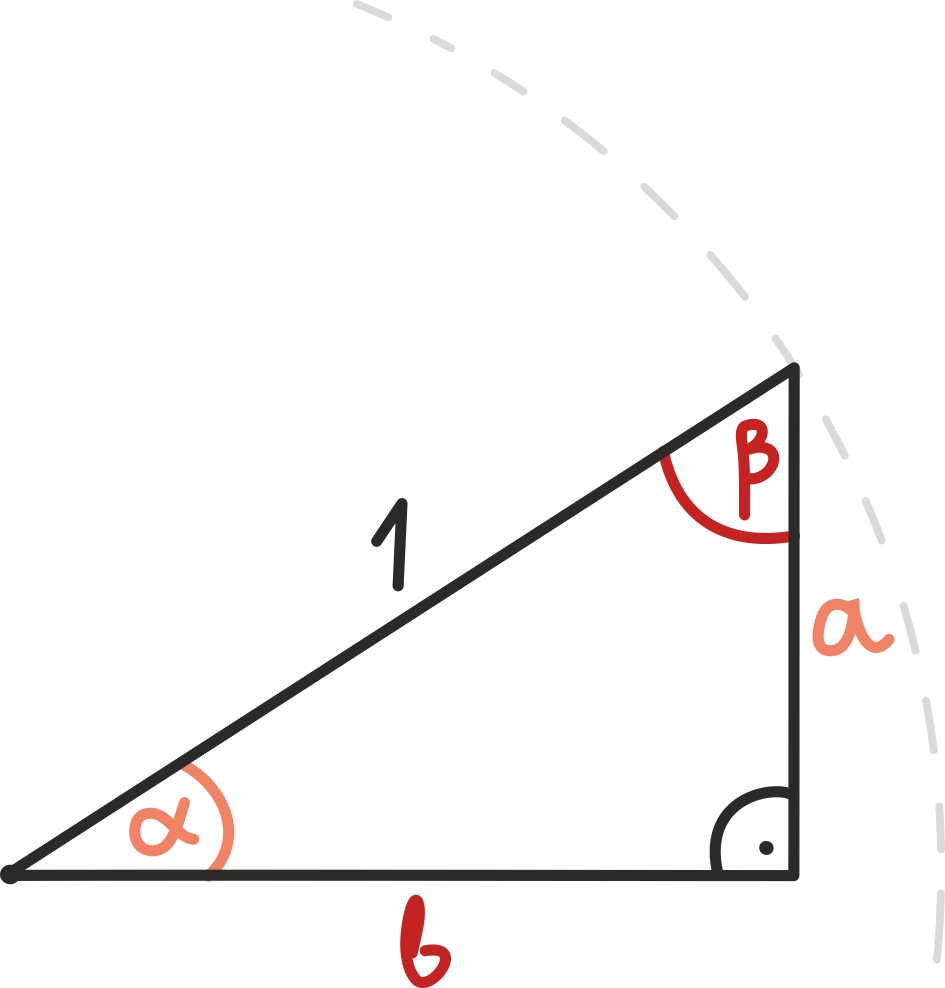
Vaatleme täisnurkset kolmnurka, mille hüpotenuusi pikkus on 1 ning mille teravnurgad on α ja β = 90º – α, täpselt sellist, millega on ka trigonomeetrilised funktsioonid defineeritud.
Esimese seose trigonomeetriliste funktsioonide vahel leiamegi juba, kui esitame kaateti a pikkuse kahel viisil.
Esiteks võime seda teha nurga α ja vastaskaateti abil, saades tulemuseks sin(α). Teiseks võime kaateti α pikkuse leida ka nurga β ja lähiskaateti abil, saades cos(β). Kuna β = 90º – α, saamegi
Teise tuntuima seose saame Pythagorase teoreemist. Teame, et täisnurkses kolmnurgas on kaatetite pikkuste ruutude summa võrdne hüpotenuusi pikkuse ruuduga
Samas võime kirjutada
Asendades need väärtused Pythagorase teoreemi, saamegi, et
Graafikute ilusatest omadustest pärit seosed
Järgnevalt vaatame aga valemeid, mis on seotud trigonomeetriliste funktsioonide graafikute ilusate omadustega.
Tuletame meelde, et funktsiooni graafiku teisendamine on aidanud meil ennegi funktsioonist aimu saada – näiteks näeme varsti, kuidas ruutfunktsiooni lahendivalemi taga on mingis mõttes tegelikult peidus lihtsad geomeetrilised teisendused [lk 278].
Trigonomeetriliste funktsioonide korral tuleb jällegi funktsiooni graafiku teisendamine suuresti abiks – nimelt on siinus- ja koosinusfunktsiooni graafikud mitmete geomeetriliste teisenduste suhtes invariantsed ehk teisisõnu neid parajal määral nihutades ja peegeldades saame jälle uuesti samad funktsioonid. Nii aitab teisenduste raames mõtlemine hästi meeles hoida siinus- ning koosinusfunktsiooniga seotud valemeid.
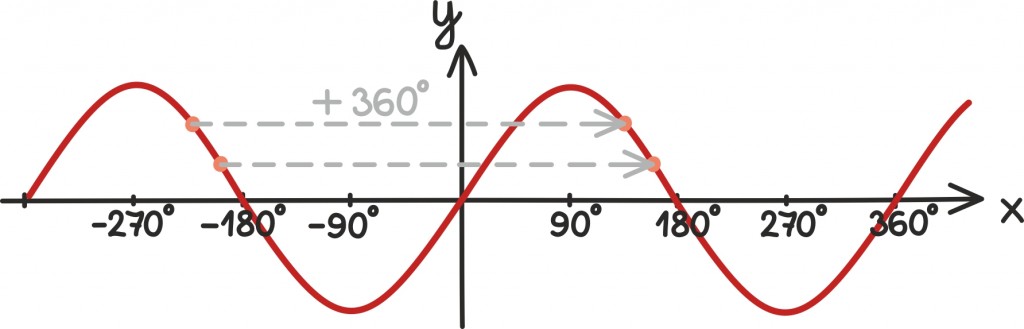
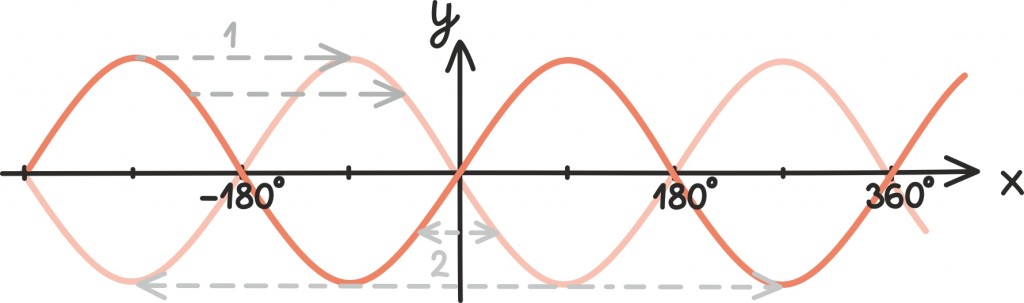
Nimelt, joonise abil on end kerge veenda, et siinusfunktsioon on perioodiline – nihutades tema graafikut täispöörde ehk 360º võrra emmas-kummas suunas, saame taas tagasi siinusfunktsiooni graafiku
Sellest järeldub, et
Lisaks on siinusfunktsioonil teatav sümmeetria x-telje suhtes – graafikut poole täispöörde ehk 180º võrra emmas-kummas suunas nihutades ning siis x-teljest peegeldades saame jälle siinusfunktsiooni graafiku.
Sellest järeldub, et
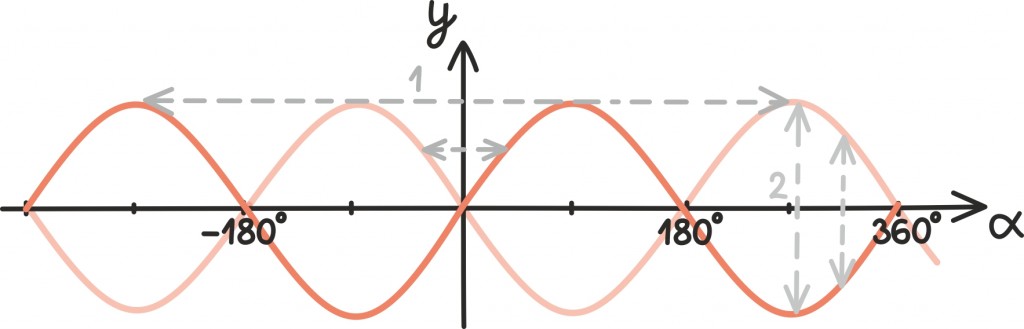
Veel on seal teatav sümmeetria ka y-telje suhtes – graafikut 180º võrra emmas- kummas suunas nihutades ja siis y-teljest peegeldades saame tagasi siinusfunktsiooni graafiku.
Meenutame, et peegeldamine y-telje suhtes juhtub, kui argument läbi korrutada arvuga –1, ning paremale poole liikumine toimub, kui argumendist lahutada (mitte liita) mingi suurus. Näiteks kui liigutame graafikut paremale, siis sellest järeldub, et
Siinusfunktsiooni graafikut järjepanu vertikaal- ning horisontaaltelgedest peegeldades saame jälle tagasi siinusfunktsiooni graafiku.
Järelikult
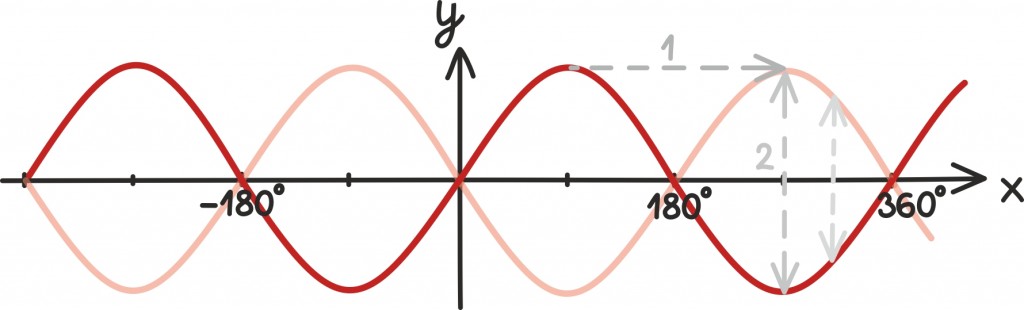
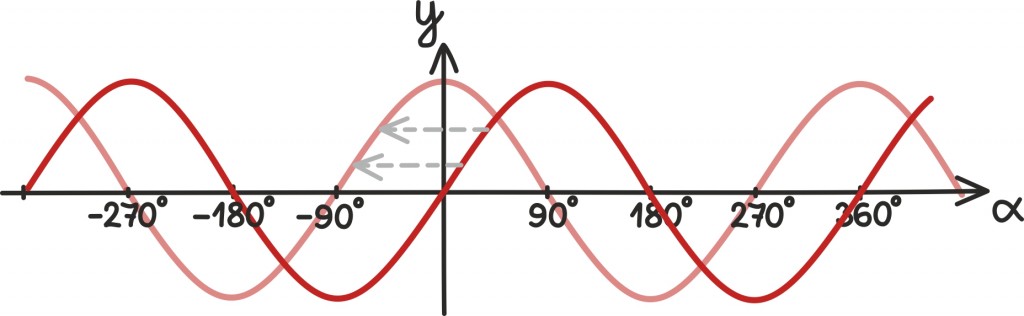
Kõigele lisaks on siinus- ning koosinusfunktsiooni graafikud samasugused: nihutades siinusfunktsiooni graafikut veerandpöörde ehk võrra vasemale, saame koosinusfunktsiooni graafiku.
Sellest järeldub, et
Kasutades lisaks ka eelnevat omadust, mis ütleb, et sin(180º – α) = sin(α), leiame taas kord ka peatüki alguses leitud teada-tuntud seose:
Samuti näeme nüüd, et see valem ei kehti sugugi ainult teravnurksete nurkade, vaid kõikvõimalike nurkade korral. Süda on rahulik, kui kõik klapib!
Kõik need omadused vajaksid tegelikult tõestuseid ning neid tõestuseid pole sugugi väga keeruline kokku keevitada: tuleb vaid tõlkida funktsiooni graafikute teisendused ühikringjoone teisendusteks ning kasutada siinus- ja koosinusfunktsioonide omadusi.
Valemite meeldejätmiseks piisab aga sellest, kui neid omadusi usute, ja ega oma silm ju ei peta!
Täpselt analoogiliselt võime mängida ka koosinusfunktsiooniga ning tuletada jällegi terve ämbritäie valemeid. Kõik nad võiks muidugi välja lugeda ka kasutades lihtsalt viimasena kirjeldatud omadusest saadud seost siinus- ja koosinusfunktsioonide abil. Mõned neist valemitest:
Viimaks, kui peaks tekkima suur huvi lisaks teada ka tangensfunktsiooni valemeid, tuleb meil eelnevaga kombineerida tangensfunktsiooni kirjutus kujus
Näiteks
Seosed nurkade liitmise ja lahutamise kaudu*
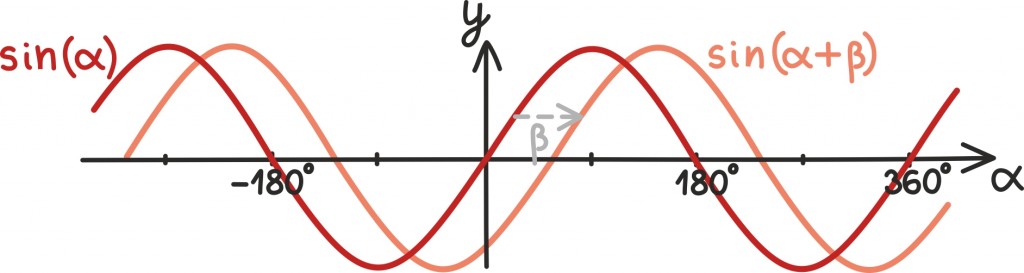
Eelmises alapeatükis nägime, kuidas siinusfunktsiooni graafikut hoolikalt nihutades ja peegeldades saame tulemuseks jällegi siinusfunktsiooni või mõnikord ka koosinusfunktsiooni graafiku. Kas meil õnnestuks aga kuidagi kirjeldada ka funktsiooni, mille graafikuks on suvalisel määral nihutatud siinusfunktsiooni graafik?
Näiteks kui nihutame funktsiooni sin(α) vasemale βkraadi võrra, saame funktsiooni sin(α + β). Kas seda õnnestub kuidagi kirjutada baasfunktsioonide sin(α), sin(β), cos(α) ja cos(β) abil?
Tuleb välja, et see on igati võimalik. Meenutame, et siinus- ja koosinusfunktsioon andsid meile võimaluse seostada kolmnurga nurgad külgede suhetega. Veelgi enam, näiteks täisnurkses kolmnurgas hüpotenuusiga 1 ongi kaks kaatetit pikkustega sin(α) ja cos(α).
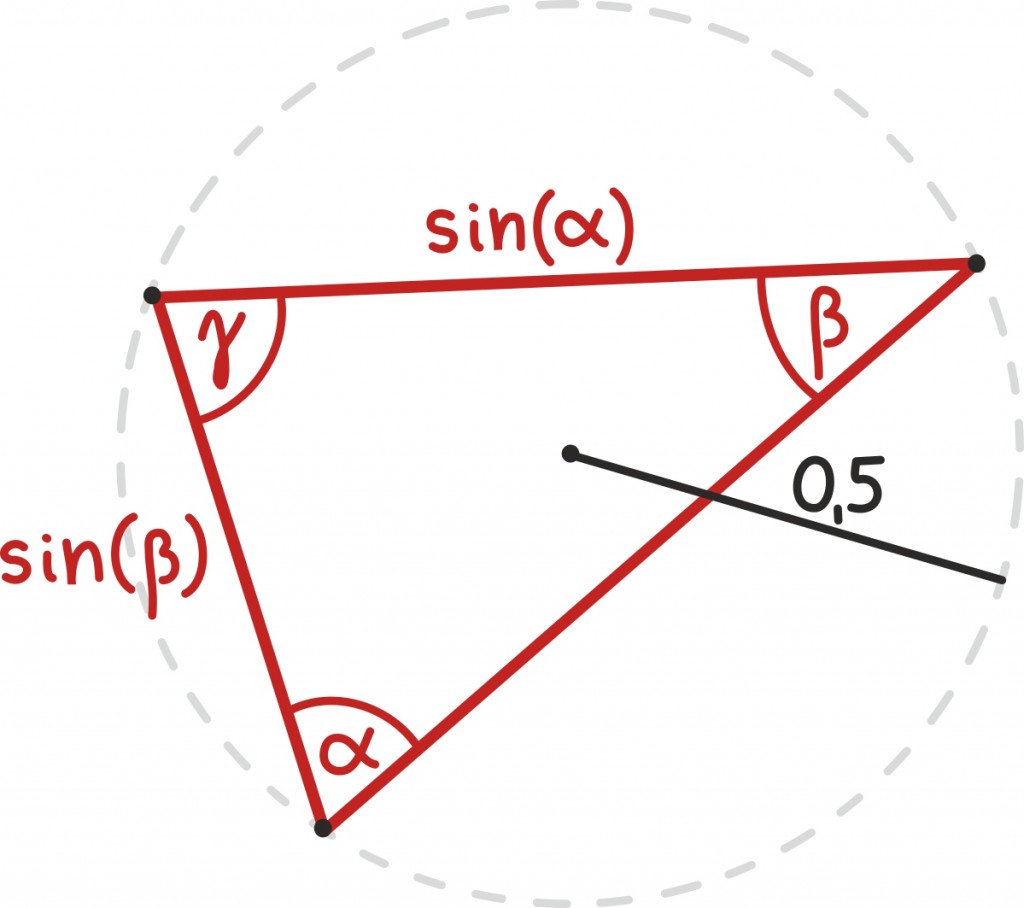
Kui tahaksime samasse kolmnurka paigutada nii nurgad α ja β, kui ka küljepikkused sin(α), sin(β) peame olema ainult veidi kavalamad. Esmalt oletame lihtsustuseks, et nurgad α ja β on teravnurksed – siis võime kindlasti konstrueerida kolmnurga, millel on täpselt kaks nurka α ja β. Nende vastasküljed a ja b võime seejärel leida laiendatud siinusteoreemist [lk 222]:
kus R on kolmnurga ümberringjoone raadius. Seega, kui valiksime kolmnurga, mille ümberringjoone diameeter on pikkusega üks, olekski nurkade α ja βvastas küljed pikkustega sin(α) ning sin(β).
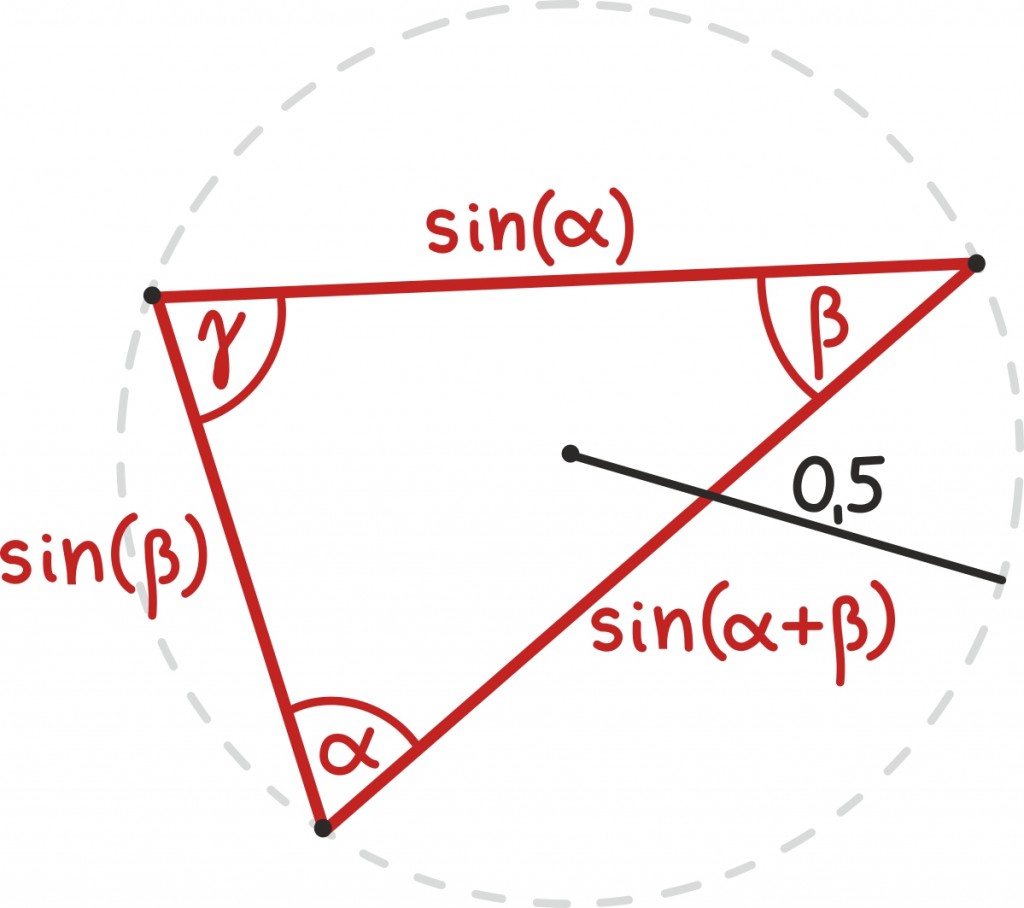
See on juba üsna hea algus. Päris rõõmsaks teeb aga tähelepanek, et kolmnurga kolmas nurk on ju
ning eespool leitud valemite põhjal kehtib võrdus
Seega, kasutades veel kord laiendatud siinusteoreemi, näeme, et kolmas, puuduv külg on täpselt pikkusega (α + β). Nüüd on üsna selge, et siit jooniselt saame ilusaid valemeid.
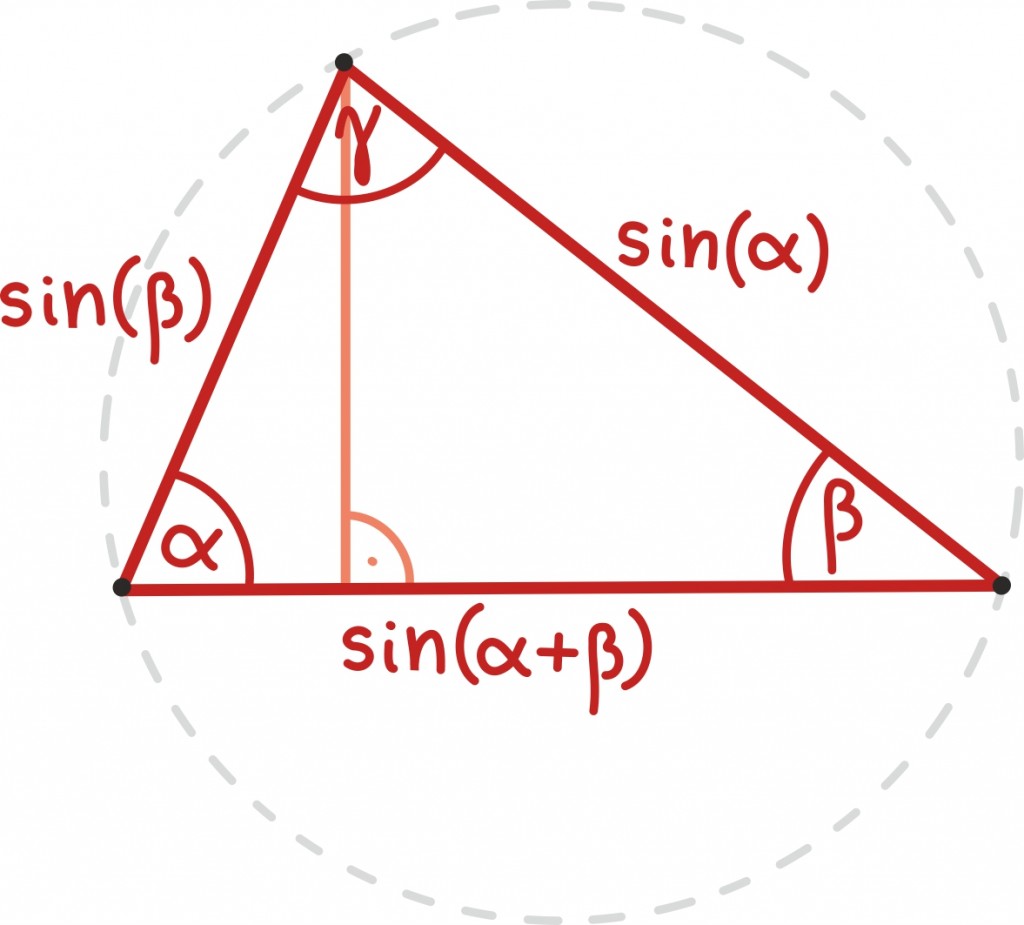
Nagu siinus- ning koosinusteoreemi tõestuste juureski, on trigonomeetriliste funktsioonidega mängides alati hea mõte tõmmata üks kõrgus, seekord siis küljele pikkusega sin(α + β).
Meie kolmnurk jaguneb nüüd kaheks täisnurkseks kolmnurgaks, millest ühe hüpotenuus on sin(α) ning alusnurk β, ning teise hüpotenuus on sin(β) ning alusnurk α.
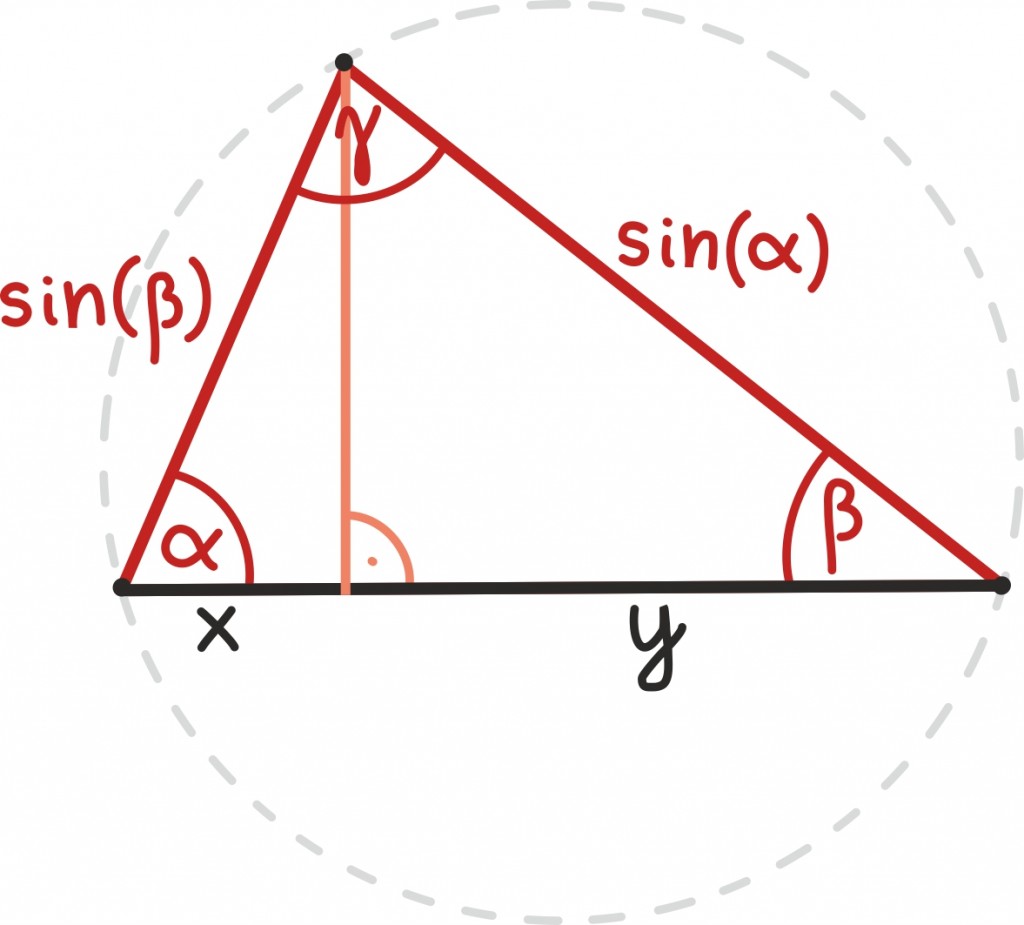
Kasutades trigonomeetrilisi seoseid neis mõlemas täisnurkses kolmnurgas, võime leida, kui pikkadeks tükkideks kõrgus vaadeldava külje jagab:
Pikkuse x saame leida järgnevalt:
järelikult
Sarnaselt saame leida ka pikkuse y.
Kuna nende tükkide pikkuste summa annab külje enda pikkuse, olemegi tuletanud valemi
Praegu tõesti tegime seda küll ainult teravnurksete nurkade α ja β jaoks, ent kasutades eelmise alapeatüki valemeid, võib lugeja end veenda, et valem kehtib suvaliste nurkade α ja β jaoks.
Siit edasi on üsna kerge tuletada ka nurkade vahe valem, kirjutades α – β = α + (–β):
kus teises võrduses kasutasime jällegi eelmise alapeatüki valemeid.
Topeltnurga 2α lihtsustava valemi leidmine on seejärel veelgi lihtsam – asendame summa valemisse β = α:
Poolnurga valemiga vajame veel veidi kannatust!
Nimelt üritame enne leida ka koosinuse summavalemi ehk kirjutada cos(α + β) lahti sin(α), sin(β), cos(α) ja cos(β) abil.
Seda võime teha, kombineerides mitmeid meile juba teadaolevaid võtteid
Asendades β = α, leiame siit ka koosinuse topeltnurga valemi:
Seades aga β = –α, leiame, et
ehk teisisõnu oleme taas tuletanud Pythagorase teoreemist tuleneva seose siinus- ja koosinusfunktsiooni vahel.
Koosinuse topeltnurga valemist on lihtne omakorda tuletada poolnurgavalemid: seades α = ½γ, leiame, et
Kasutades nüüd Pythagorase teoreemist pärinevat seost, võime selle kirjutada kahes erinevas kujus:
Neid valemeid läheb meil hiljem vaja siinusfunktsiooni tuletise leidmiseks. Lisaks saame nende abil välja kirjutada ka niinimetatud poolnurga valemid:
kusjuures märgi ruutjuurele peame valima olenevalt sellest, kui suur nurk
parasjagu on.
Viimaks heidame lühikese pilgu ka tangensile. Nagu ikka, pole meil siin muud taktikat, kui lihtsalt siinuse ja koosinuse valemeid ära kasutada. Kirjutame
Nüüd tahaksime hädasti siit segadusest üles leida funktsioonid tan(α) ja tan(β). Selle jaoks jagame lihtsalt nii murru nimetaja kui lugeja läbi korrutisega cos(α) cos(β)
Saamegi kohe
Ehk teisisõnu
Analoogselt võiksime leida ka nurkade vahe, topeltnurga ja muud kooliõpikuis figureerivad valemid. Siinkohal sai meil aga jaks otsa.
Trigonomeetriliste funktsioonide liitmine ja lahutamine*
Seni rääkisime, mis juhtub, kui teeme tehteid trigonomeetriliste funktsioonide argumendiga. Teisisõnu tuletasime lihtsustavaid valemeid näiteks nurkade summa siinuse sin(α + β) või poolnurga siinuse
jaoks.
Samas võiks aga ka küsida, kas õnnestub kuidagi teisiti kirjutada ka tehteid funktsioonide endaga.
Näiteks kõrvutades valemeid
näeme, et neid kokku liites kaob üks liige hoopis ära ja saame:
Selle võime kirjutada kujus:
või asendades α + β = γ, α – β = μ ka kujus
See on väga kena! Oleme näidanud, et koosinusfunktsioonide korrutise võib lahti kirjutada nende summana ning vastupidi. Sama kehtib muidugi ka siinusfunktsiooni kohta ja suurema vaeva korral leiame valemeid ka tangensfunktsiooni tarvis.
Kui selle kõige tarvilikkus tundub esmapilgul ka küsitav, siis aitab see näiteks paremini mõista, kuidas ikkagi toimib AM-raadio [lk 259].
Siinusfunktsiooni tuletis*
Kuna trigonomeetrilised funktsioonid on peidus pea iga perioodilise liikumise kirjeldamisel, siis osutub oluliseks ka nende funktsioonide muutumise kiirus ehk tuletis. Näiteks on meil endalgi tarvis see tuletis välja arvutada, kui asume leidma, kuidas ikka veepommi kõige kaugemale visata [lk 333]. Nagu juba mainisime, on trigonomeetriliste funktsioonide tuletiste leidmisel kasulikum kasutada radiaane [lk 234], niisiis seda teemegi.
Eelteadmised
Siinusfunktsiooni tuletise võtmiseks on (lisaks tuletisest arusaamisele [lk 320]) vaja kasutada kahte juba tuletatud trigonomeetrilist valemit:
Lisaks peame kasutama teadmist, et kui x on mõõdetud radiaanides, siis väga väikeste argumendi x väärtuste korral on sin(x) umbes võrdnex-iga. Täpsemalt, kehtib järgmine piirväärtuste [lk 313] abil kirjapandud seos:
Miks see nii on, selgitasime intuitiivselt juba ühes eelnevas peatükis [lk 99].
Tuletuskäik
Asume nüüd julgelt sin(x) tuletist leidma, lähtudes täpselt tuletise definitsioonist [lk 321]:
Kasutades siinuste summavalemit, võime selle omakorda kirjutada kui
Edasi on kaval murru nimetaja ümber kirjutada kahte ossa ning kuna summa piirväärtus on igal mõistlikul juhul võrdne piirväärtuste summaga, saame
Järgmisena võime ainult liikmega x seotud olevad väärtused piirväärtusest välja tõsta – nad ei sõltu ju sellest, mis me parajasti muutujaga d pihta hakkame:
Nüüd kasutame esimese liikme jaoks valemit 2) ning teise jaoks seost 3) ja saame:
Viimaks võime esimeses liikmes veel korra kasutada seost 3), seekord funktsiooni
jaoks:
Asendades selle juba leitud valemisse, näeme, et esimene liige on piirprotsessis võrdne
ga:
Kuid me teame, et siinusfunktsioon on pidev ning võrdne nulliga kohal null. Seega on ka piirprotsessis, kus d ise muutub nulliks, esimese liikme väärtus null.
Nii jääb piirprotsessis alles ainult teine liige ning saamegi
Huh, tehtud! Siinusfunktsiooni tuletis on koosinusfunktsioon. Tuletus on sisuliselt ainult viis rida pikk, aga nõudis siiski kahte trigonomeetrilist avaldist.
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!