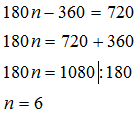HULKNURGA SISENURKADE SUMMA
Hulknurga jaotamisel ühest tipust lähtuvate diagonaalidega tekib alati kahe võrra vähem kolmnurki kui hulknurgal on nurki. Üldiselt, kui hulknurgal on n nurka, siis see hulknurk tükeldub ühest tipust väljuvate diagonaalidega (n – 2)-ks kolmnurgaks. Iga kolmnurga nurkade summa on aga 180°.
Sulle võivad huvi pakkuda need õppematerjalid:
Liitmine ja lahutamine 10 piires
Ruutvõrrandi mõiste, ruutvõrrandi lahendivalem, ruutvõrrandi liigid
Väike algebraamps
Kirjeldav statistika
Kell ja kellaaeg
Funktsioonid ja nende graafikud
Valik harjutusülesandeid matemaatika riigieksamiks
Peastarvutamine I kooliastmele
Allar Veelmaa videotund. Avaldised
Liitmine ja lahutamine 20 piires
Peastarvutamine eelkoolile
II kooliastme matemaatika reeglite kordamine
NUPUTAME KOOS! Tasapinnalised kujundid
Funktsioonide graafikud
8. klassi matemaatika teooriavideod
Geomeetria
Tasandilised kujundid
Üksliikmed, hulkliikmed ja tehted nendega
Liitmine 10 piires
Funktsioonide graafikute lõikepunktide leidmine
Nende kolmnurkade nurkade summad kokku on siis ![]() .
.
Tähistades nurkade summa tähega s saame valemi: ![]() .
.
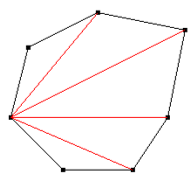
Näide 1: Leia seitsenurga sisenurkade summa.
Lahendus: Joonisel on seitsenurk ühest tipust lähtuvate diagonaalide abil jaotatud viieks kolmnurgaks. See tähendab, et tekkis kahe võrra vähem kolmnurki, kui on seitsenurgal nurki.
Sisenurkade summa peaks olema ![]() .
.
Leiame sisenurkade summa ka valemi abil: ![]() .
.
Vastus: seitsenurga sisenurkade summa on 900°.
Näide 2. Hulknurga sisenurkade summa on 720°. Leia, milline on see hulknurk.
Lahendus: Siin on s = 720° ja tippude arv ehk n on tundmatu. Seega saame valemi abil võrrandi n suhtes (jätame ära kraadimärgid): ![]()
Avame sulud ja lahendame võrrandi:
Vastus: Hulknurk, mille nurkade summa on 720°, on kuusnurk.
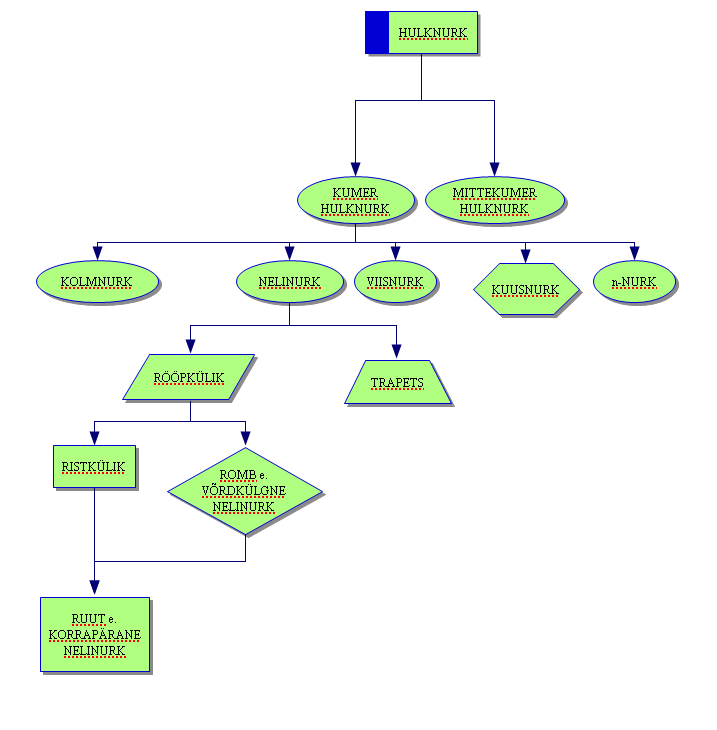
Hulknurkade liigitus:
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!