Korrapärane hulknurk
Kolmnurki, nelinurki, viisnurki jne. nimetatakse ühise nimetusega hulknurkadeks. Vaata allolevat joonist.
Hulknurk on piiratud murdjoonega. Selle murdjoone lülisid nimetatakse hulknurga külgedeks. Külgede otspunktid on hulknurga tipud.
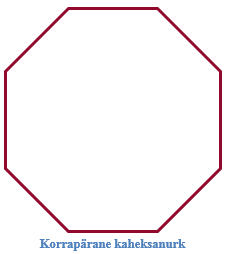
Hulknurka, millel on võrdsed küljed ja võrdsed nurgad, nimetatakse korrapäraseks hulknurgaks.
Korrapärased hulknurgad on näiteks võrdkülgne kolmnurk, ruut, korrapärane viisnurk, korrapärane kuusnurk jne. Külgede arvu (või tippude arvu) tähistame tähisega n.
Kõrvaloleval joonisel on näiteks korrapärane kaheksanurk.
Sulle võivad huvi pakkuda need õppematerjalid:
Funktsioonid ja nende graafikud
Kirjalik liitmine
Algebralised murrud
Peastarvutamine I kooliastmele
Harjutusülesandeid matemaatika riigieksamiks
Liitmine 10 piires
Lahutamine 20 piires
Tasandilised kujundid
Liitmine 20 piires
Üksliikmed, hulkliikmed ja tehted nendega
Liitmine ja lahutamine 20 piires
Kirjalik lahutamine
Ruutvõrrand
Hariliku murru kordamine
8. klassi matemaatika teooriavideod
Ruumilised kujundid
Liitmine ja lahutamine 10 piires
Funktsioonide graafikud
Ruutvõrrandi mõiste, ruutvõrrandi lahendivalem, ruutvõrrandi liigid
Ratsionaalavaldised
Korrapärase hulknurga sisenurkade summa:
Korrapärase hulknurga sisenurkade summa:
Seega ühe sisenurga suuruse saame:
Näide: Leia korrapärase kaheksanurga ühe sisenurga suurus:
Siin n = 8. Saan valemist ![]() kaheksanurga sisenurkade summa:
kaheksanurga sisenurkade summa:
Leian ühe nurga suuruse jagades sisenurkade summa kaheksaga:
Vastus: Kaheksanurga ühe sisenurga suurus on 135°.
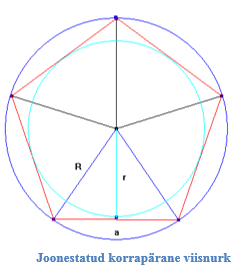
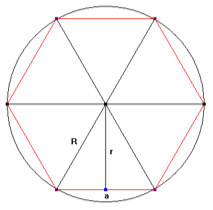
Ringjoont, mis läbib hulknurga kõiki tippe, nimetatakse hulknurga ümberringjooneks. Ümberringjoone raadiust tähistame tähisega R.
Ringjoont, mis puudutab hulknurga kõiki külgi, nimetatakse hulknurga siseringjooneks. Siseringjoone raadiust tähistame tähisega r.
Siseringjoone raadiust nimetatakse ka hulknurga apoteemiks.
Hulknurga külge tähistame sümboliga a.
Korrapärase hulknurga joonestamine sirkli, malli ja joonlaua abil:
- Arvutame välja küljele vastava kesknurga suuruse.
Kuna kesknurki on samapalju kui külgi (tähistame tähisega n) ja need on omavahel võrdsed, siis üks kesknurk moodustab täispöördest 360° : n osa.
(Näiteks viisnurga korral tuleb kesknurga suuruseks 360° : 5 = 720 )
- Joonestame ringjoone ja sellesse leitud suurusega kesknurga.
- Võtame sirklisse kesknurgale vastava kõõlu pikkuse ja märgime ringjoonel sirkliga sammudes vajalikud jaotuspunktid.
- Ühendades jaotuspunktid järjestikku kõõludega, saamegi korrapärase hulknurga.
Ringjoone jaotamisel saadud korrapärase hulknurga külgedeks on kõõlud. Seepärast nimetatakse sellist hulknurka ka kõõlhulknurgaks.
Korrapärase hulknurga ümbermõõt
Korrapärase hulknurga ümbermõõt on võrdne tema külgede pikkuse ja külgede arvu korrutisega:
Korrapärase hulknurga pindala
Et korrapärane hulknurk jaguneb niimitmeks võrdseks kolmnurgaks, kui tal on külgi, siis saame korrapärase hulknurga pindala korrutades külgede arvu ühe tekkinud kolmnurga pindalaga.
Et apoteem ehk siseringjoone raadius tähistab kolmnurga kõrgust, saame korrapärase hulknurga pindala valemiks:
Kasutatakse ka valemit, mis sisaldab poolt ümbermõõtu. Et P = na, siis saame valemi ![]() . Tähistame
. Tähistame ![]() (võrdub poolega ümbermõõdust), saame pindala valemiks poole ümbermõõdu ja hulknurga siseringjoone raadiuse (apoteemi) korrutise:
(võrdub poolega ümbermõõdust), saame pindala valemiks poole ümbermõõdu ja hulknurga siseringjoone raadiuse (apoteemi) korrutise: