Kõvertrapets
Täpsema tulemuse pindalast saaksime, kui oskaksime leida ka poolikute ruutude pindalasid. Kõiki pinnatükke saab tükeldada kõvertrapetsiteks.
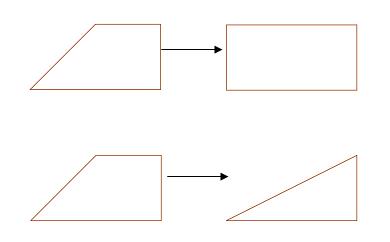
Täisnurkne trapets läheneb oma kujult ristkülikule, kui ühe aluse pikkus läheneb teise omale.
Seepärast loetakse kõvertrapetsite hulka kuuluvaiks ka ristkülikust saadav kujund, kui üks tema külg asendada kaarega ja täisnurksest kolmnurgast saadav kujund, kui tema hüpotenuus asendada kaarega.
Sulle võivad huvi pakkuda need õppematerjalid:
Liitmine 20 piires
alates 2.90 €
1. klass, 2. klass, Iseõppijale, Matemaatika
Funktsioonid ja nende graafikud
alates 6.90 €
9. klass, Iseõppijale, Matemaatika
Numbrilised seosed
alates 2.90 €
9. klass, Iseõppijale, Matemaatika
Ruutvõrrand
alates 6.90 €
9. klass, Iseõppijale, Matemaatika
xy-koordinaatsüsteem
alates 2.90 €
9. klass, Iseõppijale, Matemaatika
Ruutvõrrandi mõiste, ruutvõrrandi lahendivalem, ruutvõrrandi liigid
alates 4.90 €
9. klass, Iseõppijale, Matemaatika
8. klassi matemaatika teooriavideod
alates 4.90 €
8. klass, Iseõppijale, Matemaatika
Geomeetria
alates 6.90 €
9. klass, Iseõppijale, Matemaatika
Hariliku murru kordamine
alates 2.90 €
9. klass, Iseõppijale, Matemaatika
Funktsioonide graafikud
alates 2.90 €
9. klass, Iseõppijale, Matemaatika
Algebralised murrud
alates 5.90 €
9. klass, Iseõppijale, Matemaatika
Lahutamine 20 piires
alates 2.90 €
1. klass, 2. klass, Iseõppijale, Matemaatika
Ruumilised kujundid
alates 3.90 €
9. klass, Iseõppijale, Matemaatika
Harjutusülesandeid matemaatika riigieksamiks
alates 2.90 €
Gümnaasium, Iseõppijale, Matemaatika
Peastarvutamine I kooliastmele
alates 2.90 €
1. klass, 2. klass, 3. klass, Iseõppijale, Matemaatika
Väike protsendiamps
alates 9.90 €
6. klass, 7. klass, 8. klass, 9. klass, Iseõppijale, Täiendõppijale, Matemaatika
Ruutvõrrandi abil lahenduvad tekstülesanded
alates 1.90 €
9. klass, Iseõppijale, Matemaatika
II kooliastme matemaatika reeglite kordamine
alates 4.90 €
4. klass, 5. klass, 6. klass, Iseõppijale, Matemaatika
Ratsionaalavaldised
alates 6.90 €
9. klass, Iseõppijale, Matemaatika
Funktsioonide graafikute lõikepunktide leidmine
alates 2.90 €
9. klass, Iseõppijale, Matemaatika
Eelmine
Järgmine
Täisnurkne trapets, ristkülik ja täisnurkne kolmnurk on seega kõvertrapetsi erijuhud.
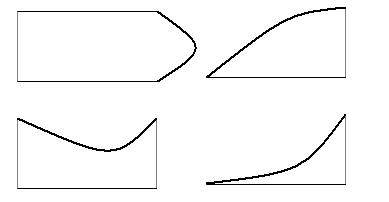
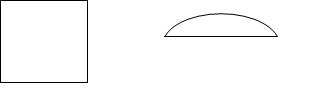
Kõvertrapetsiteks loetakse ka järgnevaid kujundeid:
See artikkel on retsenseerimata.
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!
