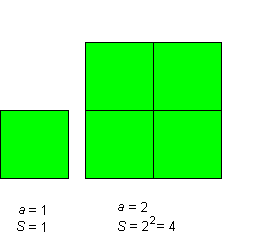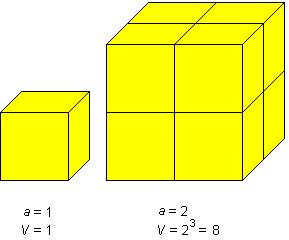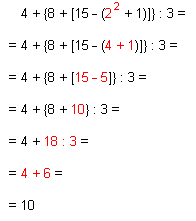Naturaalarvude korrutamine ja jagamine
Naturaalarvude korrutamine
| 2 | · | 3 | = | 6 | ||||
| tegur | tegur | korrutis | ||||||
 |
||||||||
| korrutis | ||||||||
Ühekohalise arvuga korrutamise põhiülesanded 100 piires võiks meelde jätta.
Lisainfo
Järguühikuga korrutamisel tuleb naturaalarvudele lisada juurde nii mitu nulli, kui palju on neid järguühikutes.
Näiteid.
100 · 39 = 39 000
256 · 10 = 2560
10 000 · 3729 = 37 290 000
Mitmekohaliste arvude kirjalik korrutamine.
Näide. (Nähtav arvutis)
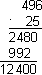
Korrutamise erijuhte
1 · a = a · 1 = a näiteks 1 · 3 = 3 · 1 = 1 + 1 + 1 = 3
0 · a = a · 0 = 0 näiteks 0 · 4 = 4 · 0 = 0 + 0 + 0 + 0 = 0
0 · 0 = 0
Sulle võivad huvi pakkuda need õppematerjalid:
Lahutamine 20 piires
Liitmine 10 piires
Hariliku murru kordamine
Funktsioonide graafikud
Funktsioonid ja nende graafikud
Harjutusülesandeid matemaatika riigieksamiks
Üksliikmed, hulkliikmed ja tehted nendega
Funktsioonide graafikute lõikepunktide leidmine
II kooliastme matemaatika reeglite kordamine
Numbrilised seosed
Peastarvutamine eelkoolile
Ruutjuur, tehted ruutjuurtega
Kell ja kellaaeg
Tasandilised kujundid
Kirjalik liitmine
Peastarvutamine I kooliastmele
8. klassi matemaatika teooriavideod
Liitmine 20 piires
Liitmine ja lahutamine 20 piires
Kirjalik lahutamine
Korrutamine
Korrutamiseks nimetatakse võrdsete liidetavate liitmist.
Näide.
3 + 3 + 3 + 3 + 3 = 5 · 3
Arvu kordsed
Arvu kordsed on kõik need arvud, mis antud arvuga jaguvad.
Näide.
16 ja 36 on arvu 2 kordsed, sest nad jaguvad 2-ga.
16 : 2 = 8
36 : 2 = 18
Kõik mingi arvu kordsed jaguvad selle arvuga.
Arvu ruut ja kuup
Arvu ruut ![]()
Näide 1.
Arvu 5 ruut on 25,
sest 52 = 5 · 5 = 25.
Arvu kuup ![]()
Näide 2.
Arvu 5 kuup on 125,
sest 53 = 5 · 5 · 5 = 125.
Naturaalarvude jagamine
| 6 | : | 3 | = | 2 | ||||
| jagatav | : | jagaja | = | jagatis | ||||
 |
||||||||
| jagatis | ||||||||
Ühekohalise arvuga jagamise põhiülesanded 100 piires võiks meelde jätta.
Lisainfo
Nulliga lõppeva naturaalarvu jagamisel järguühikuga tuleb naturaalarvu lõpust ära võtta nii mitu nulli, kui palju on neid selles järguühikus.
Näited.
27 500 : 10 = 2750
27 500 : 100 = 275
Enne jagamist on kasulik hinnata, kas arv jagub täpselt või tekib jääk.
Kuidas seda teha, leiab tabelist jaguvuse tunnused.
Mitmekohaliste arvude kirjalik jagamine
Näide. (Nähtav arvutis)
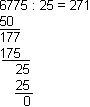
Jagamise erijuhte.
| a : 1 = a | näiteks 3 : 1 = 3 | |
| 0 : a = 0 | näiteks 0 : 2 = 0 | |
| a : a = 1 | näiteks 3 : 3 = 1 | |
| a : 0 ei ole võimalik. |
Korrutamise ja jagamise vahelised seosed
Jagamiseks nimetatakse korrutise ja ühe teguri järgi teise teguri leidmist.
Jagamise õigsust saame kontrollida korrutamise abil.
12 : 2 = 6
Kontroll. 2 · 6 = 12
Neid arve seob neli võrdust.
2 · 6 = 12
6 · 2 = 12
12 : 2 = 6
12 : 6 = 2
Jaguvus
Kui ühe naturaalarvu jagamisel teisega saadakse tulemuseks naturaalarv, siis öeldakse, et esimene arv jagub teisega.
Naturaalarvude jagamisel
1) arvud jaguvad täpselt või
2) tekib jagamisel jääk.
Näide 1.
35 : 5 = 7
Arv 35 jagub 5-ga, sest jagamisel jääki ei teki. Vaata, kuidas 35 jagub 5-ga. (Nähtav arvutis)
Näide 2.
9 : 4 = 2, jääk 1
Arv 9 ei jagu 4-ga, sest jagamisel tekib jääk. Vaata, kuidas tekib jääk. (Nähtav arvutis)
Naturaalarvude jagamisel on võimalik eelnevalt hinnata, kas tulemuseks on naturaalarv või tekib jagamisel jääk. Selleks kasutatakse jaguvuse tunnuseid.
Jaguvuse tunnused
Kui ühe naturaalarvu jagamisel teisega saadakse tulemuseks naturaalarv, siis öeldakse, et esimene arv jagub teisega.
| Millega jagub | Jaguvuse tunnus |
| 2-ga | Arv jagub kahega siis, kui arvu üheliste number on paarisnumber. Paarisnumbrid on: 0, 2, 4, 6 ja 8 Näide. Arv 356 jagub 2-ga, sest tema üheliste number on paarisnumber. |
| 3-ga | Arv jagub kolmega siis, kui arvu ristsumma jagub kolmega. Näide. Arv 264 jagub 3-ga, sest tema ristsumma (numbrite summa) on 2 + 6 + 4 = 12 ja 12 jagub 3-ga. |
| 4-ga | Arv jagub neljaga siis, kui arv lõpeb kahe nulliga või tema kaks viimast numbrit moodustavad arvu, mis jagub neljaga. Näide. Arv 5624 jagub 4-ga, sest tema kaks viimast numbrit moodustavad arvu 24, mis jagub 4-ga. |
| 5-ga | Arv jagub viiega siis, kui tema üheliste number on 0 või 5. Näide. Arv 6520 jagub 5-ga, sest tema üheliste kohal on number 0. |
| 6-ga | Arv jagub kuuega siis, kui ta jagub 2-ga ja 3-ga. Näide. Arv 630 jagub 6-ga, sest arv 630 jagub 2-ga ja 3-ga. |
| 7-ga | Arv jagub seitsmega siis, kui arvu kolmest viimasest numbrist moodustatud arvu ja ülejäänud numbritest moodustatud arvu vahe (või vastupidi) jagub seitsmega. Näide. Arv 251 321 jagub 7-ga, sest vahe 321 – 251 = 70 jagub 7-ga. |
| 8-ga | Arv jagub kaheksaga siis, kui arv lõpeb kolme nulliga või tema kolmest viimasest numbrist moodustatud arv jagub kaheksaga. Näide. Arv 7000 jagub 8-ga, sest tema 3 viimast numbrit on nullid. |
| 9-ga | Arv jagub üheksaga siis, kui arvu ristsumma (numbrite summa) jagub üheksaga. Näide. Arv 2736 jagub 9-ga, sest arvu ristsumma on 2 + 7 + 3 + 6 = 18 ning 18 jagub 9-ga. |
| 10-ga | Arv jagub kümnega siis, kui arvu üheliste number on null. Näide. Arv 7590 jagub 10-ga, sest arvu üheliste number on null. |
| 11-ga | Arv jagub 11-ga siis, kui arvu kolmest viimasest numbrist moodustatud arvu ja ülejäänud numbritest moodustatud arvu vahe (või vastupidi) jagub 11-ga. Näide. Arv 211 112 jagub 11-ga, sest vahe 211 – 112 = 99 jagub 11-ga. |
| 12-ga | Arv jagub 12-ga siis, kui ta jagub 3-ga ja 4-ga. Näide. Arv 624 jagub 12-ga, sest arv 624 jagub 3-ga ja 4-ga. |
| 13-ga | Arv jagub 13-ga siis, kui arvu kolmest viimasest numbrist moodustatud arvu ja ülejäänud numbritest moodustatud arvu vahe (või vastupidi) jagub 13-ga. Näide. Arv 32 123 jagub 13-ga, sest vahe 123 – 32 = 91 jagub 13-ga. |
| 18-ga | Arv jagub 18-ga siis, kui ta jagub 2-ga ja 9-ga. Näide. Arv 2736 jagub 18-ga, sest ta jagub 2-ga ja 9-ga. |
| 25-ga | Arv jagub 25-ga siis, kui tema kaks viimast numbrit on nullid või moodustavad arvu 25, 50 või 75. Näide. Arv 218 975 jagub 25-ga, sest tema kaks viimast numbrit moodustavad arvu 75. |
| 50-ga | Arv jagub 50-ga siis, kui tema kaks viimast numbrit on nullid või moodustavad arvu 50. Näide. Arv 6 387 250 jagub 50-ga, sest tema kaks viimast numbrit moodustavad arvu 50. |
Vaata lisaks: Arvutamise seadused
Tehete järjekord
Kui avaldises on astendamist, korrutamis-, jagamis-, liitmis- ja lahutamistehteid, siis arvutatakse avaldise väärtus järgmises järjekorras:
- astendatakse,
- korrutatakse või jagatakse (tehete esinemise järjekorras),
- liidetakse või lahutatakse (tehete esinemise järjekorras).
Kui avaldises on ka sulud, siis tehakse esmalt sulgudes olevad tehted.
Kui avaldises on erinevates sulgudes olevaid tehteid, siis tehakse tehted esmalt ümarsulgudes, siis nurksulgudes ja seejärel looksulgudes