PÜSTRÖÖPTAHUKAS, SELLE PINDALA JA RUUMALA
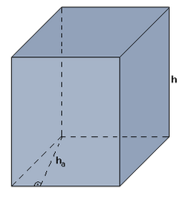
Püströöptahukas on püstprisma, mille põhjadeks on võrdsed rööpkülikud ja külgtahkudeks ristkülikud.
Risttahukas on püströöptahuka erijuht, sest risttahuka põhjadeks on ristkülikud, mis on rööpküliku erijuht (rööpkülik, mille nurgad on 90°).
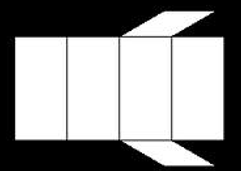
Alloleval joonisel on püströöptahuka pinnalaotus.
Sulle võivad huvi pakkuda need õppematerjalid:
Liitmine 10 piires
Numbrilised seosed
Väike protsendiamps
Allar Veelmaa videotund. Avaldised
Valik harjutusülesandeid matemaatika riigieksamiks
Peastarvutamine eelkoolile
NUPUTAME KOOS! Tasapinnalised kujundid
Algebralised murrud
Funktsioonid ja nende graafikud
Ruutvõrrandi mõiste, ruutvõrrandi lahendivalem, ruutvõrrandi liigid
Ruutvõrrand
Lahutamine 20 piires
Kirjalik liitmine
Kirjeldav statistika
Geomeetria
Funktsioonide graafikud
Liitmine 20 piires
xy-koordinaatsüsteem
Funktsioonide graafikute lõikepunktide leidmine
Üksliikmed, hulkliikmed ja tehted nendega
Pinnalaotuse pindala on püströöptahuka täispindala ja külgtahkudeks olevate ristkülikute pindala kokku nimetatakse külgpindalaks.
Külgpindala leidmine – püströöptahuka külgpindala võrdub põhja ümbermõõdu ja püströöptahuka kõrguse korrutisega.
Valem: Sk = PH
Täispindala leidmiseks tuleb külgpindala liita kahekordne põhja pindala ehk rööpküliku pindala Sp=ah
Valem: St= Sk+2 Sp
Püströöptahuka ruumala leidmine – Püströöptahuka ruumala võrdub põhja pindala ja püströöptahuka kõrguse korrutisega.
Valem: V = Sp ∙ H
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!