Igapäevases elus kasutatakse täpseid ja ligikaudseid arve. Täpsed arvud saadakse loendamise teel või arvutamisel täpsete arvudega. Ligikaudsed arvud saadakse mõõtmisel, ümardamisel või arvutamisel ligikaudsete arvudega.

Igal mõõtmisega kaasneb mingi mõõtmisviga, mida pole võimalik täielikult vältida. Need vead võivad olla põhjustatud mõõtevahendist, mõõtmisviisist, mõõdetava eseme iseärasustest ja tingimustest, milles mõõtmine läbi viidi jne. Kõik mõõtmistulemused on seega ligikaudsed!

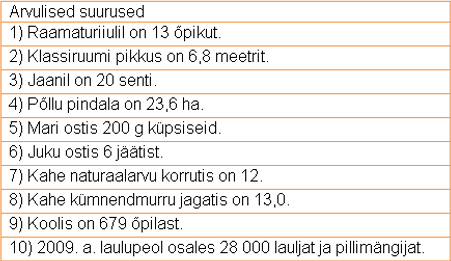
N: Otsusta, millised suurused on tabelis täpsed arvud ja millised ligikaudsed.

Vastus: 1) täpne, 2) ligikaudne, 3) täpne, 4) ligikaudne, 5) ligikaudne, 6) täpne, 7) täpne, 8) ligikaudne (ümardatud vastus), 9) täpne, 10) ligikaudne

Arvutamisel tuleb paljudel juhtudel tulemusi ümardada, mistõttu saame samuti ligikaudseid arve.

Et ümardamisel tekkiv viga oleks võimalikult väike, siis on kokku lepitud ümardada ülespoole, kui esimene ärajääv number on 5, 6, 7, 8 või 9 ja arv ei muutu siis, kui see number on 0, 1, 2, 3 või 4.

Täisarvu ümardamisel asendatakse kõik kõrvaldatud numbrid nullidega, kümnendmurru murdosast kõrvaldatud järgud jäetakse kirjutamata. Ümardamisel saadud arvu nimetatakse esialgse arvu lähendiks.

N:

Ümarda arv 123 450 tuhandelisteni:

Ümarda arv 12,5678 sajandikeni:

Ümardatud kümnendmurru lõpunulle ei tohi jätta kirjutamata, sest järk, milleni ümardatakse, tuleb lähendis säilitada.

N: Ümarda arv 32,951 kümnendikeni:

Arvu esitamine liigse täpsusega ei ole mõistlik. Selle tulemusel võivad muutuda arvutused liiga töömahukaks.

Lisaks

Harjuta