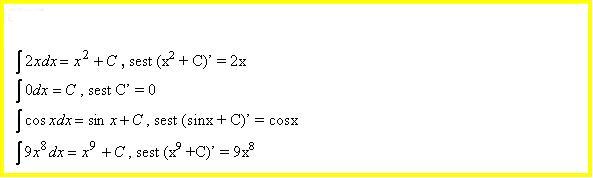Määramata integraal
Funktsiooni algfunktsiooni leidmist nimetatakse funktsiooni integreerimiseks.
Integrare (lad. k) – taastama, täiendama.
Integreerimine on seega funktsiooni diferentseerimise pöördoperatsioon.
Loe: integraal ef iks de iks
Muutujat x nimetatakse integreerimismuutujaks, avaldist f(x)dx integreeritavaks avaldiseks, funktsiooni f(x) integreeritavaks funktsiooniks ning avaldisi F(x) + C ja ![]()
Sulle võivad huvi pakkuda need õppematerjalid:
Liitmine ja lahutamine 10 piires
Väike algebraamps
Tasandilised kujundid
Kirjalik lahutamine
xy-koordinaatsüsteem
Liitmine ja lahutamine 20 piires
Ruumilised kujundid
Protsendi rakendused igapäevaelus
Ruutvõrrandi abil lahenduvad tekstülesanded
Ruutjuur, tehted ruutjuurtega
Kirjeldav statistika
II kooliastme matemaatika reeglite kordamine
Valik harjutusülesandeid matemaatika riigieksamiks
Funktsioonide graafikud
Allar Veelmaa videotund. Avaldised
Ratsionaalavaldised
8. klassi matemaatika teooriavideod
Funktsioonide graafikute lõikepunktide leidmine
NUPUTAME KOOS! Tasapinnalised kujundid
Peastarvutamine I kooliastmele
Sõna määramata tähendab, et integraal sisaldab suvalist konstanti.
Loe lisaks määramata integraali mõiste:
Näide
Integreeritav avaldis f(x)dx on algfunktsioonide üldavaldise diferentsiaal.
Kokkuvõte:
Diferentseerides leitakse antud funktsiooni kaudu tema tuletis. Integreerides leitakse funktsioon tema tuletise kaudu. Seega on diferentseerimine ja integreerimine teineteise pöördoperatsioonid funktsioonide hulgas.
Diferentseerimine on ühene seos: kui funktsioonil on tuletis, siis ainult üks.
Integreerimine ei ole ühene: kui funktsioonil on algfunktsioon, siis on tal lõpmata palju algfunktsioone.
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!