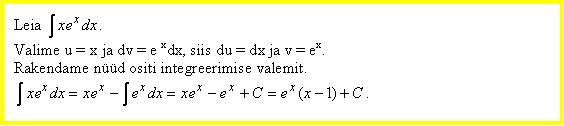Ositi integreerimine

Teiseks integreerimist lihtsustavaks võtteks on ositi integreerimise võte, mille eesmärgiks on uute muutujate sissetoomisega jõuda lihtsamate integreeritavate avaldisteni. Ositi integreerimise valem:

Ositi integreerimist kasutatakse selliste funktsioonide korral, kus integreeritavaks avaldiseks on xⁿe^x, xⁿsinx, xⁿcosx, xⁿlnx või mõne trigonomeetrilise funktsiooni pöördfunktsioon. Sel juhul valitakse u = xⁿ, kus n on naturaalarv.

See ei lahenda ülesannet lõpuni, vaid taandab ühe integraali () leidmise teise integraali () leidmisele.

Ositi integreerimist kasutatakse tavaliselt siis, kui integraali all on kahe funktsiooni korrutis, millest üks on kas

• astme- või eksponent- või trigonomeetriline funktsioon;

• arkus- või logaritmfunktsioon.

Näited:

Ositi_integreerimine