PÖÖRDVÕRDELINE SÕLTUVUS, PÖÖRDVÕRDELISE SÕLTUVUSE GRAAFIK
Kui kahe muutuja vastavate väärtuste korrutis on jääv, nimetatakse nendevahelist seost pöördvõrdeliseks sõltuvuseks.
Sümbolites: 
ehk 
ja 
.
Öeldakse, et funktsiooni y väärtused on pöördvõrdelises seoses muutuja x vastavate väärtustega.
See tähendab, et ühe muutuja väärtuste suurenemisel (vähenemisel), väheneb (suureneb) teise muutuja väärtus sama arv korda.
Pöördvõrdelise seose graafikut nimetatakse hüperbooliks.
Pöördvõrdelise seose graafik – hüperbool
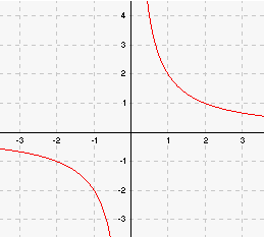
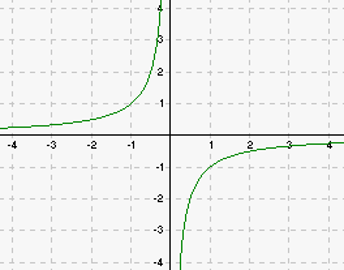
Kui pöördvõrdelise seoses a>0, siis asub graafik koordinaattasandi I ja III veerandis, kui a<0, siis II ja IV veerandis.
Alloleval joonisel (Joonis 1) on kujutatud pöördvõrdelise seose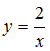 
graafik.
Joonis 1
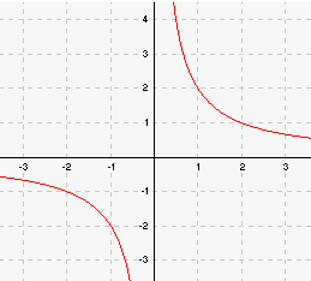
Alloleval joonisel (Joonis 2) on kujutatud pöördvõrdelise seose 
graafik.
Joonis 2
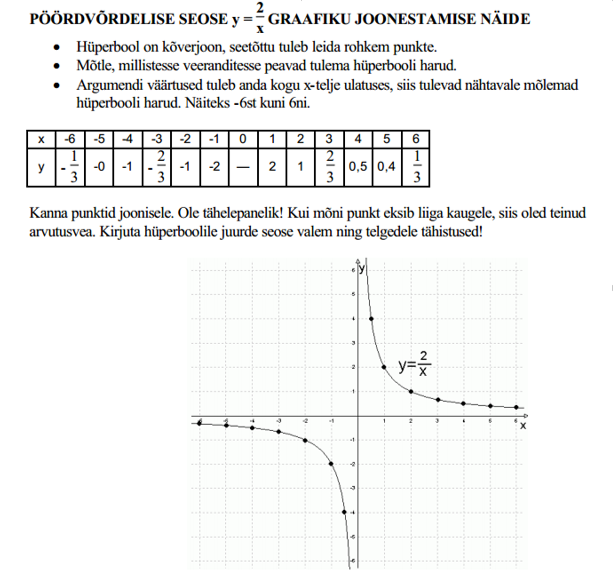
Pöördvõrdelise seose graafiku joonestamise näide:
TESTID:
