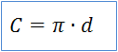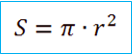Ring ja ringjoon

Ringjoone kõik punktid asetsevad ühel ja samal tasandil ning nad on ringjoone keskpunktist võrdsel kaugusel. Ringjoone raadiuse saame ühendades ringjoone keskpunkt ja ringjoone mingi punkt sirglõiguga.

Ringjoone diameetriks nimetatakse lõiku, mis läbib ringjoone keskpunkti ja ühendab ringjoone kahte punkti, mida täistatakse tähega d. Diameeter on raadiusest kaks korda pikem. Seda pannakse kirja valemiga: d = 2 r .

Lõiku, mis ühendab kahte ringjoone punkti, nimetatakse kõõluks. Diameeter on ringi keskpunkti läbib kõõl. Diameeter on ringi suurim kõõl.

Ringjoone kahte punkti vahelist osa nimetatakse ringjoone kaareks.

Pildi allikas

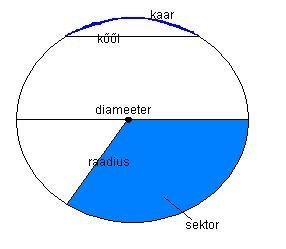
Ringjoone kõik punktid asetsevad ringjoone keskpunktist ühel ja samal kaugusel.

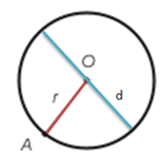
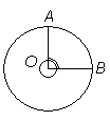
Ringjoone raadiuseks nimetatakse ringjoone keskpunkti ja ringjoone mistahes punktiga ühendatud lõiku (ja ka selle lõigu pikkust).

Raadiust tähistatakse tähega r.

Lõiku, mis läbib ringjoone keskpunkti ja ühendab kahte ringjoone punkti, nimetatakse ringjoone diameetriks.

Sulle võivad huvi pakkuda need õppematerjalid:

Diameetrit tähistatakse tähega d ning see on raadiusest kaks korda pikem: d = 2 ∙ r

Ringjoon ja selle pikkus

Juba kauges minevikus märkasid teadlased, et iga ringjoone pikkus on kindel arv kordi pikem selle diameetrist. Seda arvu tähistati kreeka väiketähega π (loe: pii). Arv π on lõpmatu mitteperioodiline kümnendmurd, mille mõned esimesed kohad on sellised:

π = 3,14159265358973238462643383…

Ülesannete lahendamisel kasutame selle ligikaudset väärtust: π≈3,14.

Arvu π abil saame ringjoone pikkuse ehk ringi ümbermõõdu arvutamise valemi:

Et ringjoone diameeter on raadiusest kaks korda pikem, võime valemile anda ka sellise kuju:

N: Arvutame ringjoone pikkuse, kui ringi raadius on 5 cm.

C ≈ 2 • 3,14 • 5 = 31,4 (cm)

Vastus. Ringjoone pikkus on 31,4 cm.

Video arvu π saamisest:

Ring ja ringi pindala

Ringi moodustab ringjoone sees olev tasandi osa koos ringjoonega.

Ringjoone raadius ja diameeter on ühtlasi ringi raadius ja diameeter.

Ringi pindala arvutamiseks tuleb π korrutada raadiuse ruuduga.

N: Arvutame ringi pindala, kui ringi raadius on 5 cm.

S ≈ 3,14 • 5² = 78,5 (cm²)

Vastus. Ringi pindala on 78,5 cm².

Ingliskeelne video ringi pindala valemi tuletamisest:

Sektordiagramm

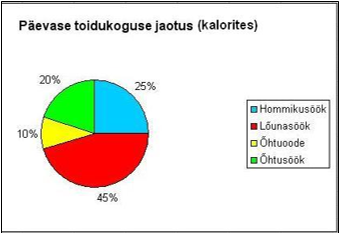
Sektordiagramm on diagramm, milles arve kujutavad ringi sektorid. Sektordiagrammi kasutatakse peamiselt protsentide kujutamiseks.

Kui joonestada ringile kaks raadiust, jagavad need ringi kaheks osaks. Mõlemat osa nimetatakse ringi sektoriks.

Ring moodustab täispöörde. Täispööre on 360^o.

Osa ringist saame väljendada protsentides.

1%-le täispöördest vastab 360^o : 100 = 3,6^o.

N: Pildil näide sektordiagrammist:

N: Teises näites saab valida rippmenüüst erineva poiste ja tüdrukute arvu klassis, kus on kokku 24 õpilast. Vastavalt valitud andmetele muutub nuppu vajutades diagramm.

Näite vaatamiseks vajuta siia.

Harjuta ülesandeid ringjoone pikkuse, ringi pindala ja sektordiagrammi kohta

Kordavad testid ringi ja ringjoone kohta:

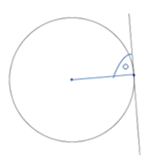
Ringjoone puutuja

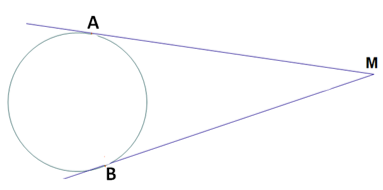
Ringjoone puutuja on risti puutepunkti tõmmatud raadiusega.