RUUTFUNKTSIOON

Ruutfunktsioon avaldub kujul y = ax²+ bx + c, kus a, b ja c on mistahes arvud ja ruutliikme kordaja a ≠ 0.

Ruutfunktsiooni y = ax²+ bx + c graafikuks on parabool.

Kui ruutliikme kordaja a > 0, siis parabooli harud avanevad üles, kui a < 0, siis alla.

Parabooli sümmeetriatelge nimetatakse parabooli teljeks ja punkti, kus parabool lõikub oma teljega nimetatakse parabooli haripunktiks.

Parabooli skitseerimiseks tuleb leida nullkohad ( võrrandi ax²+ bx + c = 0 lahendid) ja haripunkt ( haripunkti abstsissi ehk x väärtuse leiame kas nullkohtade aritmeetilise keskmisena või valemist .

Ordinaadi ehk y väärtuse leidmiseks paneme abstsissi väärtuse funktsiooni avaldisse ning leiame y väärtuse.

Parabool läbib y-telge punktis (0 ; c). Vajadusel arvutame veel lisapunkte juurde.

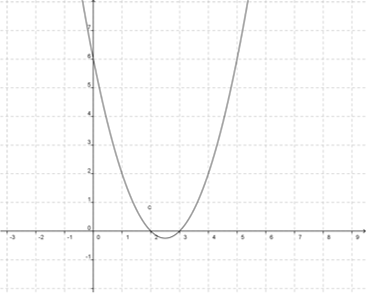
Näide. Skitseerime ruutfunktsiooni y = x²– 5x + 6 graafiku. Graafik avaneb ülespoole, kuna ruutliikme kordaja on positiivne (a = 1). Graafiku skitseerimiseks leiame esmalt nullkohad, st. ruutvõrrandi x²– 5x + 6 = 0 lahendid.

Viete´i teoreemi põhjal saame x1= 2 ja x2 = 3. Graafiku haripunkti leiame nullkohtade aritmeetilise keskmisena ja

Seega saadud haripunkti koordinaadid on H(2,5; -0,25).

Parabool läbib y-telge punktis (0 ; 6). Lisaks saame märkida parabooli teljega sümmeetrilise punkti (5;6). Oleks soovitav arvutada ka paar lisapunkti. Näiteks (1;2) ja sellega sümmeetriliselt (4;2). Skitseerime joonise:

Skeem parabooli joonestamiseks:

määran parabooli avanemise suuna (üles või alla)
leian haripunkti koordinaadid
leian nullkohad (kui need on olemas)
koostan väärtuste tabeli, võttes x väärtused väiksemast nullkohast 1-2 võrra väiksemast arvust kuni suuremast nullkohast 1-2 võrra suurema arvuni.
kui nullkohti ei ole, siis võtan 3-4 x väärtust, mis on haripunkti koordinaadist väiksemad ja sama palju x väärtusi, mis on haripunkti x koordinaadist suuremad.

Vaata lisaks:

Ruutfunktsiooni graafik