Tõenäosusteooria põhimõisted
Põhimõisted ja seosed nende vahel
Lähtemõisteks on tõenäosusteoorias sündmus.
Sündmused on näiteks täringuga kuue silma heitmine, eksamil hinde “5” saamine, lotopiletiga võitmine jms. Sündmuste tõeväärtust peab saama määrata. Näiteks lause – “Jüri on loll” ei ole matemaatilises mõttes sündmus, kuna objektiivselt pole võimalik lause tõeväärtust määrata. Samuti ei sündmus vihma sadamine, kui jäetakse märkimata, kus see toimub jne.
Sulle võivad huvi pakkuda need õppematerjalid:
Peastarvutamine I kooliastmele
Lahutamine 20 piires
xy-koordinaatsüsteem
Protsendid põhikooli matemaatikas
Ratsionaalavaldised
Liitmine ja lahutamine 10 piires
Liitmine 10 piires
Ruutvõrrand
II kooliastme matemaatika reeglite kordamine
Ruutjuur, tehted ruutjuurtega
Kell ja kellaaeg
Geomeetria
Liitmine ja lahutamine 20 piires
NUPUTAME KOOS! Tasapinnalised kujundid
Tasandilised kujundid
Liitmine 20 piires
Üksliikmed, hulkliikmed ja tehted nendega
Funktsioonid ja nende graafikud
Valik harjutusülesandeid matemaatika riigieksamiks
Numbrilised seosed
Sündmusi liigitatakse juhuslikeks, kindlateks ja võimatuteks.
Sündmusi tähistatakse suurte ladina tähtedega A, B, C, … jne. Kindlat sündmust tähistatakse tähega Ω ja võimatu sündmuse tähistamiseks kasutatakse tühja hulga märki Ø.
Sündmused on võrdvõimalikud, kui nende esiletuleku (toimumise) võimalused on ühesugused. Näiteks mündi pildumisel on kulli ja kirja esiletuleku võimalused võrdsed. Loteriil võitmine või mittevõitmine pole võrdvõimalikud, sest võidupileteid on müüdud piletitega võrreldes tühiselt vähe.
Juhuslikke sündmusi nimetatakse üksteist välistavateks, kui nad ei saa korraga toimuda. Kui saate eksamil “viie”, siis “kolme” sellel eksamil ei saa saada.
Sündmuse A vastandsündmuseks on sündmus Ã, mis toimub siis, kui sündmus A ei toimu. Kui sündmus A on 5 saamine täringuheitel, siis sündmus à on 1, 2, 3, 4 või 6 silma saamine.
Sündmuse A tõenäosuseks nimetatakse sündmuse jaoks soodsate võimaluste arvu m ja kõigi võimaluste arvu n suhet, s.t.
Jätke meelde, et p(Ω) = 1 ja p(Ø) = 0.
Tõenäosuste summa ja korrutis
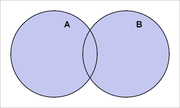
Kahe sündmuse A ja B summaks nimetatakse sündmust, mille toimumine seisneb kas sündmuse A võ B või mõlema toimumises.
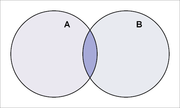
Kahe sündmuse A ja B korrutiseks nimetatakse sündmust, mille toimumine seisneb sündmuse A ja B toimumises.
Tõenäosuste summa ja korrutis graafiliselt:
Näide: olgu sündmus A täringul nelja silma tulek ja sündmus B paarisarvuline silmade arv. Sel juhul sündmuste A ja B
summa A U B = {2; 4; 6} ja
Allikas: Tõenäosusteooria_põhimõisted
ÜLESANDED:
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!