Absoluutväärtusega võrrand
Meie eesmärk siin raamatus ei ole alati õpetada – õpetada oskavad palju paremini õpetajad ise – vaid pigem anda ideid, kuidas koolimatemaatikast mõelda. Seega üritame ka siin pisikeses peatükis ainuüksi selgitada, kuidas absoluutväärtusega võrrandit tõlgendada. Meenutame, et arvu absoluutväärtusest kirjutasime juba ka arvude peatükis [lk 120].
Sulle võivad huvi pakkuda need õppematerjalid:
8. klassi matemaatika teooriavideod
xy-koordinaatsüsteem
Ruutjuur, tehted ruutjuurtega
Valik harjutusülesandeid matemaatika riigieksamiks
Väike protsendiamps
Protsendi rakendused igapäevaelus
Protsendid põhikooli matemaatikas
Kell ja kellaaeg
Funktsioonid ja nende graafikud
II kooliastme matemaatika reeglite kordamine
Väike algebraamps
Lahutamine 20 piires
NUPUTAME KOOS! Tasapinnalised kujundid
Funktsioonide graafikute lõikepunktide leidmine
Geomeetria
Liitmine 10 piires
Liitmine 20 piires
Ruutvõrrandi abil lahenduvad tekstülesanded
Funktsioonide graafikud
Üksliikmed, hulkliikmed ja tehted nendega
Oletame, et teid on vastamisi seatud võrrandiga:
Tundub päris hirmuäratav? Põhjuseta!
On mitu viisi, kuidas ennast veenda, et tegemist on üsna ohutu olukorraga.
Esmalt võib üritada võrrandi lahti sõnastada „kauguste” abil.
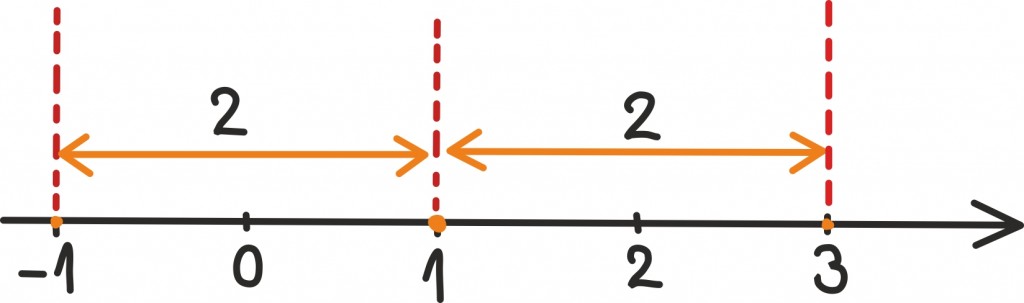
Oletame näiteks, et meil on lihtsam võrrand |x –1| = 2. Võrrandi vasak pool kirjeldab siis punkti x kaugust arvust 1 ja võrrandi lahendamine tähendab kõikide selliste punktide x leidmist arvteljel, mis on arvust 1 kahe ühiku kaugusel:
Jooniselt on lihtne näha, et võimalikud on täpselt kaks punkti: x = 3 või x = –1. Kui meile on aga antud keerulisem võrrand nagu lehekülje alguses, on joonise abil lahendamine juba päris raske. Näiteks võrrandi
võime küll lahti sõnastada kauguste abil:
- võrrandi vasak pool kirjeldab arvu x kauguste summat arvudest 2 ja 0,
- võrrandi parem pool kirjeldab arvu x kaugust arvust 1 ja lisab selle kaugusele veel 2 juurde.
Ent siiski läheb joonise abil lahendamine keeruliseks. Niisiis mõtleme korra, kuidas veel lihtsama võrrandi |x –1| = 2 lahendamisest mõelda.
Joonisel hakkame automaatselt proovima kahte erinevat juhtu:
- punkt x asub arvust 1 paremal pool
- punkt x asub arvust 1 vasemal pool
Sümbolites tähendab see aga, et me vaatasime läbi kaks juhtu:
- x – 1 on positiivne
- x – 1 on negatiivne
Kasutades absoluutväärtuse definitsiooni, annavad need kaks juhtu meile kaks erinevat võrrandit:
- x – 1 = 2
- –(x –1) = 2
On lihtne näha, et esimene annab täpselt meile vastuse 3 ja teine vastuse –1.
Täpselt sama strateegia aitab ka keerulisemate võrrandite puhul. Peame iga võrrandis asuva absoluutväärtuse jaoks vaatama läbi kaks juhtu – juhu, kus absoluutväärtuste vahel olev avaldis on positiivne, ja juhu, kus ta on negatiivne.
Nii ei erine absoluutväärtusega võrrandi lahendamine sugugi tavalise võrrandi lahendamisest – absoluutväärtusega võrrandi puhul tuleb lihtsalt läbi vaadata mitu tavalist võrrandit.
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!