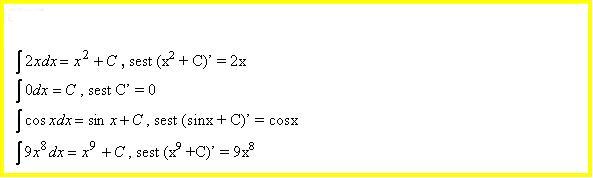Määramata integraal
Funktsiooni algfunktsiooni leidmist nimetatakse funktsiooni integreerimiseks.
Integrare (lad. k) – taastama, täiendama.
Integreerimine on seega funktsiooni diferentseerimise pöördoperatsioon.
Loe: integraal ef iks de iks
Muutujat x nimetatakse integreerimismuutujaks, avaldist f(x)dx integreeritavaks avaldiseks, funktsiooni f(x) integreeritavaks funktsiooniks ning avaldisi F(x) + C ja ![]()
Sulle võivad huvi pakkuda need õppematerjalid:
Tasandilised kujundid
Liitmine ja lahutamine 10 piires
Üksliikmed, hulkliikmed ja tehted nendega
Geomeetria
Valik harjutusülesandeid matemaatika riigieksamiks
Algebralised murrud
Allar Veelmaa videotund. Avaldised
Protsendid põhikooli matemaatikas
xy-koordinaatsüsteem
Funktsioonid ja nende graafikud
Väike algebraamps
Ratsionaalavaldised
Funktsioonide graafikud
Kirjeldav statistika
Peastarvutamine I kooliastmele
Ruutvõrrand
Ruutvõrrandi mõiste, ruutvõrrandi lahendivalem, ruutvõrrandi liigid
II kooliastme matemaatika reeglite kordamine
Kirjalik liitmine
Kirjalik lahutamine
Sõna määramata tähendab, et integraal sisaldab suvalist konstanti.
Loe lisaks määramata integraali mõiste:
Näide
Integreeritav avaldis f(x)dx on algfunktsioonide üldavaldise diferentsiaal.
Kokkuvõte:
Diferentseerides leitakse antud funktsiooni kaudu tema tuletis. Integreerides leitakse funktsioon tema tuletise kaudu. Seega on diferentseerimine ja integreerimine teineteise pöördoperatsioonid funktsioonide hulgas.
Diferentseerimine on ühene seos: kui funktsioonil on tuletis, siis ainult üks.
Integreerimine ei ole ühene: kui funktsioonil on algfunktsioon, siis on tal lõpmata palju algfunktsioone.
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!