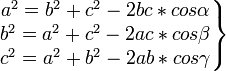Siinusteoreem
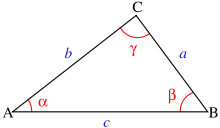
Siinusteoreem on seos kolmnurga külgede ja nurkade vahel. Selle järgi on kolmnurga suurima külje vastas ka suurim nurk.
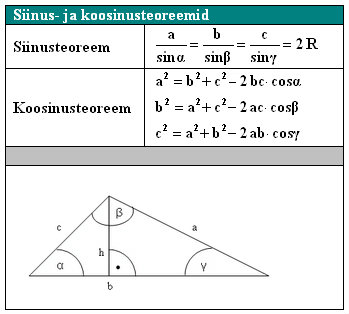
Täpsemalt öeldes on kolmnurga kõigi külgede suhe vastasnurga siinusesse konstantne ning selle kaudu saab leida kolmnurga ümberringjoone raadiuse R.
Siinusteoreemi kasutatakse kolmnurga arvutamiseks, kui on teada üks külg, selle vastasnurk ja veel kas üks külg või üks nurk. Juhul, kui on teada kaks külge ja ühe külje vastasnurk, tuleb eelnevalt veenduda ka selles, kas otsitav nurk on teravnurk või nürinurk (näiteks sin 150° = sin 30° = 0,5). Kolmnurga nurkade summa peab kokku tulema 180 kraadi.
Koosinusteoreem
Koosinusteoreem on matemaatiline teoreem trigonomeetrias, mis näitab mis tahes kolmnurga külgede suhet ühe nurgakoosinusega.
Teoreemi sõnastus: Kolmnurga ühe külje ruut on võrdne ülejäänud külgede ruutude summaga, millest on lahutatud samade külgede ja nendevahelise nurga koosinuse kahekordne korrutis.
Allikas: Siinusteoreem, Koosinusteoreem
