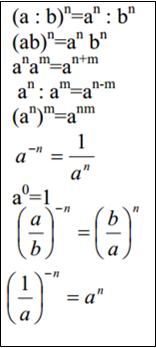TEHTED HULKLIIKMETE JA ÜKSLIIKMETEGA
Avaldiste teisendamisel kehtivad ka valemid:
Algebralise avaldise, üks- ja hulkliikme mõiste:
Algebraline avaldis on avaldis, mille väärtuse leidmiseks kasutatakse lõplik arv kordi vaid nelja aritmeetika põhitehet (liitmist, lahutamist, korrutamist, jagamist) ning astendamist ja juurimist täisarvulise astendaja ja juurijaga.
Näiteks: 2a+4a2
Üksliikmeks nimetatakse reaalarvulise teguri ja ühe või mitme muutuja naturaalarvulise astendajaga astme korrutist.
Näiteks: -5a3b
Hulkliikmeks nimetatakse üksliikmete liitmisel ja lahutamisel saadud avaldist.
Üksliikme kordajaks nimetatakse üksliikmes esinevat reaalarvulist tegurit. Kui tegur võrdub ühega, siis jäetakse ta kirjutamata. Üksliikme kordaja märki (+ või −) nimetatakse üksliikme märgiks. Üksliikme astmeks nimetatakse temas olevate muutujate astendajate summat.
Näiteks:
−7xyz3 on viienda astme üksliige, sest muutujate astendajate summa on 1 + 1 + 3 = 5;
2a on esimese astme üksliige, sest a astendaja on 1;
Üksliige 53 on nullinda astme üksliige, sest muutujat pole, ehk muutuja astendaja on 0.
Allikas ja test:
Sarnased üksliikmed, nende koondamine
Üksliikmeid nimetatakse sarnasteks, kui nad üksteisest üldse ei erine või kui nad erinevad ainult kordaja poolest.
Näiteks: Sarnased üksliikmed on 5a2bc4 ja (−0,2)7a2bc4 ning xy ja xy, kuid sarnased ei ole 2xy2 ja 2x2y.
Üksliikmete liitmisel ja lahutamisel saadud avaldist nimetatakse üksliikmete algebraliseks summaks ehk hulkliikmeks. Nii on avaldis 2x2 + 4xy − 0,75xyz − 12 hulkliige.
Üksliikmete koondamiseks nimetatakse sarnaste liikmete algebralise summa asendamist sellise liidetavatega sarnase üksliikmega, mille kordaja on võrdne liidetavate üksliikmete kordajate summaga.
Näide: koondades sarnased üksliikmed summas 2xy − 5xy + 6xy tuleb asendada see üksliikmega (2 − 5 + 6)xy = 3xy.
Hulkliikme koondamine tähendab antud hulkliikme esitamist kujul, milles kõik sarnased üksliikmed on koondatud.
Näide: koonda hulkliikmed:
4x2 − 3x + 7 − 8x2 + x − 2 = −4x2 − 2x + 5
3xy2 + 5x − 6xy2 − 2xy + 2xy2 − 5xy − z = −xy2 − 7xy + 5x − z.
Allikas ja test:
Sulle võivad huvi pakkuda need õppematerjalid:
Geomeetria
Kirjeldav statistika
Liitmine ja lahutamine 20 piires
Kell ja kellaaeg
Ratsionaalavaldised
Liitmine 10 piires
Liitmine ja lahutamine 10 piires
Funktsioonide graafikud
Valik harjutusülesandeid matemaatika riigieksamiks
Väike algebraamps
Funktsioonide graafikute lõikepunktide leidmine
Lahutamine 20 piires
Ruutjuur, tehted ruutjuurtega
Peastarvutamine I kooliastmele
Ruutvõrrand
Protsendid põhikooli matemaatikas
xy-koordinaatsüsteem
II kooliastme matemaatika reeglite kordamine
8. klassi matemaatika teooriavideod
Üksliikmed, hulkliikmed ja tehted nendega
Tehted üks- ja hulkliikmetega
Järgnevalt esitatakse näiteülesanded tehetest üks- ja hulkliikmetega.
1. Hulkliikmete summa ja vahe.
(5x2 − 4x + 3) − (3x2 − x + 2) = avame sulud
= 5x2 − 4x + 3 − 3x2 + x − 2 = koondame sarnased liidetavad (samavärvilised liidame-lahutame)
= 2x2 − 3x + 1
2. Üksliikme korrutamine üksliikmega.
6x3yz2⋅(−2xz2) = korrutame kordajad (arvud) omavahel, x-d omavahel, y-d omavahel ja z-d omavahel
= 6⋅(−2)⋅x3⋅x⋅y⋅z2⋅z2=
= −12x4yz4
3. Hulkliikme korrutamine üksliikmega.
a) (6x2 + 2xy − 3y2) ⋅ (−2x) = korrutame esimeste sulgude iga liikme teise suluga
= (6x2) ⋅ (−2x) + (2xy) ⋅ (−2x) + (−3y2) ⋅ (−2x) = korrutame üksliikmed
= −12x3 + (−4x2y) + 6xy2 = −12x3 − 4x2y + 6xy2
b) (−1) ⋅ (x7 + 2x − 3) = −(x7 + 2x − 3) = −x7 − 2x + 3
4. Hulkliikme korrutamine hulkliikmega.
(2x − y)(x3 + y2 − 2xy) = teiste sulgude iga liikme korrutame 2x-ga ja seejärel korrutame teiste sulgude iga liikme -y-ga
=(2x)⋅(x3) + (2x)⋅(y2) + (2x)⋅(−2xy) + (−y)⋅(x3) + (−y)⋅(y2) + (−y)⋅(−2xy) = korrutame üksliikmed
=2x4 + 2xy2 + (−4x2y) + (−x3y) + (−y3) + 2xy2 = koondame sarnased liikmed (no allajoonitud), avame sulud
= 2x4 + 4xy2 − 4x2y − x3y − y3
5. Üksliikme jagamine üksliikmega. (Tulemus ei ole alati üksliige)
6x2y4: (−2xy) = −3xy3 Siin jagati kordajad omavahel, x-ga liikmed omavahel, y-ga liikmed omavahel
4xy2 : (−2xy3z) = −2y−1z−1 (ei ole üksliige, sest on negatiivne astendaja vastuses, mille tähendus on ![]() jne)
jne)
6. Hulkliikme jagamine üksliikmega.
(5x3 − 6x2 + 7) : x = jagame hulkliikme iga liikme x-ga
=(5x3) : x + (−6x2) : x + 7 : x =
7. Üksliikme astendamine.
(−2x2y3z)4 = üksliikme iga liige astendatakse neljaga
=(−2)4⋅(x2)4⋅(y3)4⋅z4 = vajadusel vaadake astendamise reegleid eestpoolt (Sarnased üksliikmed, kordamine)
= 16x8y12z4
8. Hulkliikme astendamine.
a) (2a − 5)3 = kuup tähendab, et tuleb astendatavat (siin siis sulge) korrutada iseendaga kolm korda
=(2a − 5)⋅(2a − 5)⋅(2a − 5) = korrutame esimesed kaks sulgu kokku
= (4a2 − 10a − 10a + 25) ⋅ (2a − 5) = koondame esimeses sulus kaks keskmist liiget
(4a2 − 20a + 25) ⋅ (2a − 5) = korrutame need hulkliikmed (sulud), selleks korrutame esimeste sulgude esimese liikmega teised sulud ja siis esimese sulu teise liikmega teised sulud ja lõpuks esimese sulu kolmanda liikmega teised sulud
= 8a3 − 20a2 − 40a2 + 100a + 50a − 125 = koondame sarnased liikmed
= 8a3 − 60a2 + 150a − 125
b) (a + b + c)2 = (a + b + c)⋅(a + b + c) =
= a2 + ab + ac + ba + b2 + bc + ca + cb+ c2 =
=a2 + b2 + c2 + 2ab + 2ac + 2bc
Allikas ja testid:
Testid:
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!