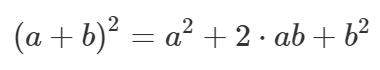Võrdus ja võrdsus
Võrdsus on igapäevane mõiste. Räägitakse võrdsetest valikutest, võrdsetest võimalustest, võrdsetest vahetustest. Seega ei ole üllatav, et võrdsus kuulub ka matemaatiliste põhimõistete alla. Matemaatika tahab aga täpsust. Mida me võrdsuse all täpsemalt silmas peame?
Teisisõnu, kui ütleme, et kaks puud on võrdse jämedusega või et kahel meeskonnal on tabelis võrdne seis või et kahte õpetajat kuulati võrdse huviga, siis mis ühendab sõna võrdne kõigis neis fraasides?
Natuke järele mõeldes tundub, et pea igas kontekstis käsitleme teatud omadusi või objekte võrdsetena, kui neid võiks omavahel ära vahetada, nii et keegi vahetusele jälile ei saaks.
Muidugi sõltub äravahetatavus päriselus detailide rohkusest, mida arvestame: kaks head õpetajat on äravahetatavad, kui meid huvitab ainult see, kui palju õpilasi neid põnevil kuulab. Kui aga arvesse võtta ka jutu sisu või nende juuksevärv, siis on neid ilmselt igati võimalik eristada.
Matemaatiline võrdsus on väga sarnane. Tahame võrdseks pidada objekte, mille äravahetamine ei muudaks mitte kübetki. Jällegi peame aga hoolsad olema ja kindlaks määrama, milliseid omadusi silmas peame. Matemaatiliselt pannakse säärane arvude võrdsus kirja matemaatilise võrduse abil.
Näiteks kahte arvu tahame lugeda võrdseteks, kui kõikides seostes teiste arvudega ning kõikide tehete suhtes käituvad nad täpselt ühtemoodi.
Näiteks on võrdsed arvud 2⁄3 ja 6⁄9, kuigi nad näevad välja erinevad. Samuti on matemaatikas arv 1 ja lõpmatu perioodilise esitusega arv 0,999 … võrdsed, ent nende kümnendesitused on ju erinevad! Seda võib endale selgitada mitmel moel. Kui arvud 1 ja 0,999 … oleksid erinevad, siis peaksid need arvud erinema mingi nullist erineva arvu võrra. Aga ükskõik kui väiksele arvule 0,999 … juurde liidame, saame ikkagi ühest suurema aru. Samuti võib tunduda mõistlik, et
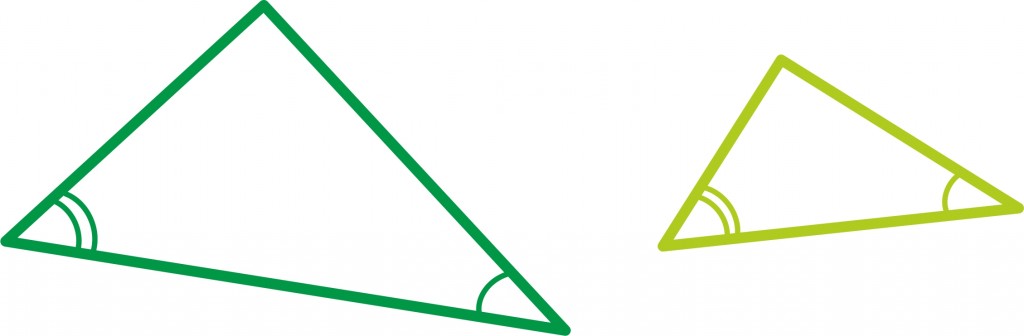
Ka paljude teiste objektide jaoks on nende võrdsus saanud eraldi nimetuse. Näiteks kahte kolmnurka, mida võime teineteise peale kattuvalt asetada ja mis seega on iga geomeetrilise teisenduse suhtes võrdsed, nimetatakse kongruentseteks kolmnurkadeks. Neil on täpselt võrdsed küljed ja nurgad.
Mõnikord huvitab meid aga ainult kolmnurkade kuju ja mitte nende täpne suurus. Kolmnurki, mida võime suurendamise ja vähendamise teel teineteiseks muuta, nimetatakse sarnasteks kolmnurkadeks.
Üks matemaatika eesmärke on leida lihtsaid tingimusi, mille korral kaks objekti on võrdsed. Nagu nägime, ei ole arvude puhul nende kümnendesitus ega ka murdesitus sobivaks kriteeriumiks. Näiteks kolmnurkade puhul selgub aga, et kahe kolmnurga võrdsuseks piisab kõigi kolme külje võrdsusest ning nende sarnasuseks kolme nurga võrdsusest.
Matemaatiline võrdus
Nagu mainisime, võime arvude võrdsuse kirja panna matemaatilise võrduse abil. Matemaatilise võrduse tähistamiseks kasutatakse lühikeste rööbaste moodi märki „=”. Näiteks võime eelnevalt väidetud arvvõrduse kirja panna kujus
Matemaatilise võrduse kasutus on muidugi laiem kui ainult arvud: arvude asemel võivad olla ka näiteks arvavaldised. Arvavaldis ei ole midagi keerulist – seal võivad arvude kõrval olla ka mõned tähed, mis võivad tähistada erinevaid arve, ja tehtemärgid.
Näiteks on arvavaldis 1 + 1 ja seega sobib ka võrduseks 1 + 1 = 2.
Keerulisem arvavaldis on näiteks a + 3b, kus a ja bvõivad tähistada suvalisi arve. Nad on seega muutujate rollis [lk 48] – nende väärtus võib meie suva järgi muutuda. Kui a tähistab arvu 1 ja b arvu 2, võime kirjutada võrduse a + 3b = 7. Seejuures peame meeles hoidma, mis ikkagi arvude ja väärtused parasjagu on. Nende väärtuseid muutes ei pruugi võrdus ju enam kehtida!
Tõese võrdusega seotud arvud või arvavaldised on iga arvutuse suhtes äravahetatavad: ükskõik mida me kahe võrdusmärgiga seotud arvu või avaldisega ei teeks, siis niikaua kui kohtleme neid täpselt samal viisil, jäävad tulemid alati võrdseks.
Näiteks võime tõsta eeltoodud võrduse märgi mõlemad pooled ruutu: (1 + 1)2 = 22 või lisada mõlemale poolele arvu 5 : 1 + 1 + 5 = 2 + 5. Võrdus jääb nii esimesel kui teisel juhul endiselt kehtima.
Võrdusmärgi tänapäevase tähise võttis kasutusele Walesi matemaatik Robert Recorde 16. sajandil – ta oli lihtsalt tüdinenud välja kirjutamast sõnapaari „on võrdne”. Sedasama võrdusmärki kasutatakse ka paljude teiste matemaatiliste objektide võrdsuse tähistamiseks, näiteks kohtame teda juba järgmises peatükis, kus ta tähistab hulkade võrdsust.
Sulle võivad huvi pakkuda need õppematerjalid:
Ruutvõrrandi abil lahenduvad tekstülesanded
Peastarvutamine eelkoolile
Protsendid põhikooli matemaatikas
Liitmine 10 piires
Ruumilised kujundid
Numbrilised seosed
Algebralised murrud
Ruutvõrrand
Liitmine ja lahutamine 20 piires
8. klassi matemaatika teooriavideod
Ratsionaalavaldised
Funktsioonid ja nende graafikud
Peastarvutamine I kooliastmele
xy-koordinaatsüsteem
Geomeetria
Liitmine ja lahutamine 10 piires
Väike protsendiamps
Harjutusülesandeid matemaatika riigieksamiks
Liitmine 20 piires
Funktsioonide graafikute lõikepunktide leidmine
Matemaatilise võrduse kasutused
Nagu nägime, on võrdus matemaatiline mõiste, mis aitab meil mõttekäiku täpsustada.
Võrdused teevad üldiselt elu lihtsamaks.Võrdusmärgiga seotud avaldised või arvud või muud matemaatilised objektid on täpselt samad. Seega võime kasutada igas olukorras meile sobivat, lihtsamat esitust.
Näiteks kui teame, et a2 – b2 = (a – b) · (a + b), annab see meile hea kavala mooduse teatud arvude korrutamiseks: Kui palju on 8 · 12? Muidu vajab see omajagu pearaginat, aga kui kirjutame 8 = 10 – 2 ning 12 = 10 + 2 , näeme, et 8 · 12 = (10 – 2) · (10 + 2). Eeltoodud võrduse põhjal on see aga võrdne arvuga 102 – 22. Kuid 10 · 10 = 100 ja 2 · 2 = 4, seega 8 · 12 = 96!
Seega nagu kirjandustunnis tahetakse, et otsiksite ühele sõnale sünonüüme, et end ilusamini väljendada, tasub alati otsida ka matemaatilisele objektile võrdseid objekte ja samaväärseid kirjeldusi. See teeb tihti matemaatika tegemise lihtsamaks: näiteks vahel soovime sama arvu näha kujus 823543, vahel aga kujus 77 – kumb esitus meeldib Sulle rohkem?
Võrdused on kasulikud ka kitsamate matemaatiliste tarkuste edasiandmisel.
Arvutustarkused ja samasus
Võrduse abil võib lühidalt esitada igasugu erinevaid arvutustarkusi, mida vahel kutsutakse ka samasusteks, et rõhutada nende igavest ja ajatut kehtimist.
Näiteks a + b = b + a väljendab, et ükskõik millise kahe arvu summa ei olene liidetavate järjekorrast. Seda nimetatakse matemaatikas kommutatiivsuseks. Tõepoolest, kui a = 2, b = 4, kordame juba eeltoodud tarkust: 2 + 4 = 4 + 2.
Kuulus teisendamisnipp
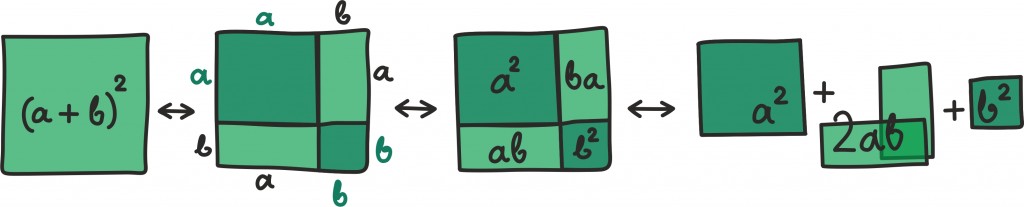
näitab, et ükskõik millise kahe arvu summa ruudu võime leida, kui liidame kokku nende arvude ruudud ja lisame sellele veel arvude kahekordse korrutise. Kas valem pole mitte lühem kui eelmine lause? Või on toredam hoopis järgmine geomeetriline kirjeldus?
Viimase pildi keskmine liige näitab, et ab ja ba on võrdsed ning nende kokkuliitmisel tekibki 2ab.
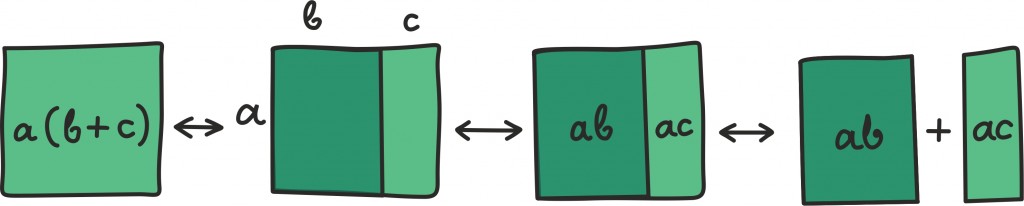
Kuna eelmine joonis on väga tore, siis tõestame ka korrutamise jaotumise ehk distributiivsuse
sarnase graafilise meetodiga:
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!