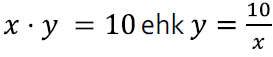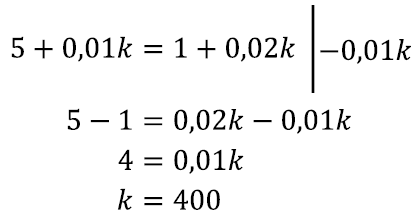Võrrand

Võrrand aitab täpselt ja matemaatiliselt kirja panna teatavaid tingimusi. See on looduse ja ümbritseva kirjeldamise esimene etapp – maailma matemaatilistesse seostesse surumine.

Oletame näiteks, et tahame ehitada uut lauluväljakut. Kõige olulisem on ehituse juures muidugi, et laulukaare alla mahuks piisavalt huvilisi. Teades, kuivõrd lauljatele meeldib ligistikku ümiseda, võib näiteks optimistlikult arvestada, et ühele trepiruutmeetrile mahub kolm lauljat.

Selle tingimuse võime matemaatiliselt kirja panna järgmiselt:

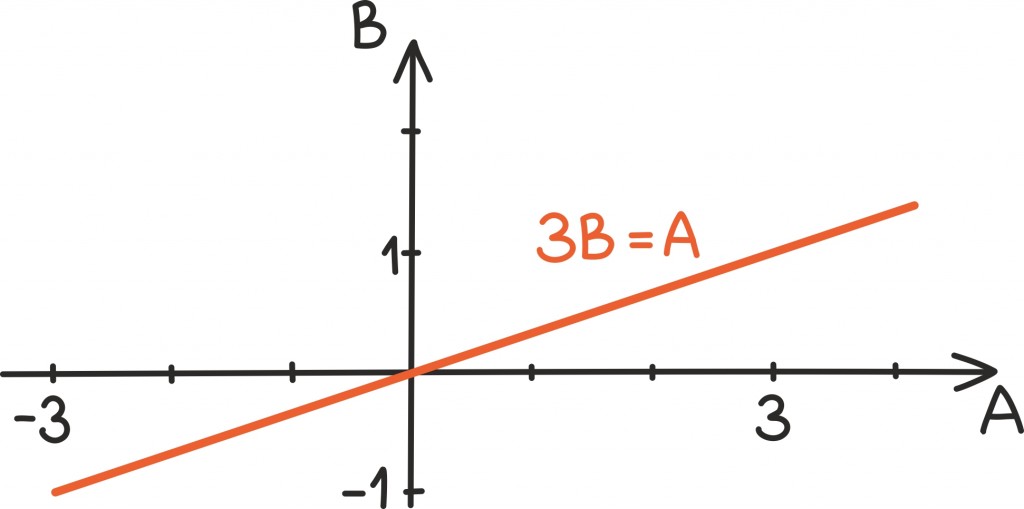
Kui meid pikk kirjutamine ära tüütab, võime võimalikku lauljate arvu tähistada A-ga, vabade ruutmeetrite arvu B-ga ning kirjutada sama võrrandi järgmiselt:

Kuigi nüüd peame hoolega meeles pidama, mida ikkagi A ja B tähistavad, on kirjutamisvaeva vähem.

Võrrandid aitavadki tingimusi ökonoomselt kirja panna ja elulisi küsimusi ümber sõnastada, nii et järele jääb ainult küsimuse jaoks oluline. Näiteks oleme ju täiesti unustanud, milline on laulupeo ajal ilm või kuidas keegi riides on, ja seda õigustatult.

Võrrandi moodustavad

mõned muutujad ehk meile veel tundmata väärtusega suurused [lk 48];
mõned arvud, mida kutsutakse kordajateks, kui nad korrutavad läbi mõnda muutujat, ning vabaliikmeteks, kui nad on omapäi;
võrdusmärk „=”, mis neid muutujaid ja arve omavahel seosesse seab.

Näiteks meie võrrandis on kaks muutujat: A ja B, arv 3 on meie võrrandis kordajaks ja ühtegi vabaliiget nagu polegi.

Kui tahaksime juurde lisada tingimuse, et 100 ruutmeetrit peab siiski ka orkestri tarvis jääma, peaksime lauljatele mõeldud ruutmeetrite arvu 100 võrra vähendama ja saaksime koos vabaliikmega võrrandi:

Muidugi tuleks lõpetuseks võrrand ka veel ära lahendada ehk leida kõik arvupaarid, mis kirjapandud võrrandit lahendavad.

Siin pole see eriti raske: seos A = 3 · B seab ju ainult piirangu, et üks arv on teisest kolm korda suurem. Nii on lahendiks näiteks A = 3, B = 1, kui A = 1200, B = 3600, kui A = –1, B = –¹⁄₃.

Nagu varsti näeme, kogunevad kõik need lahendid ühele sirgele. On kerge märgata, et mitte sugugi iga lahend ei ole enam tõlgendatav meie algülesande raames. Tõepoolest, lahendite tagasitõlkimisel elu konteksti peame jälle olema hoolikad – üks viis järgimaks, et kõik läheb sobivalt, on uurida algses ülesandes peituvaid ühikuid.

Võrrand ja ühikud

Elulise alusega võrranditel on tavaliselt kaasas ka ühikud. Näiteks rääkisime meie võrrandis ruutmeetritest ja inimestest.

Esiteks on oluline neil järge ajada, sest kui sassi lähevad 10 m/s ja 10 km/h võib ikka üsna hiljaks jääda.

Teiseks aitavad nad aru saada, kas kirja on saanud mõistlik võrrand. Nimelt võime näiteks vaadata, kas võrrandi mõlemal poolel olevad arvud kirjeldavad võrreldavaid suuruseid ehk kas neid saab loendada samades ühikutes – võrduse mõlemal poolel peavad olema ju samad ühikud.

Näiteks meie võrrandi vasakul poolel on lauljate arv ehk teatud inimeste arv. Mis on aga võrrandi paremal poolel?Esmapilgul oleks seal justkui ainult ruutmeetrite arv – pindala ühik. Siiski, tuletades meelde, et kordaja 3 tähistab inimeste arvu iga ruutmeetri kohta, saame ikkagi ühikuks inimeste arvu:

Võrrandite matemaatilise lahendamise ajaks võib aga ühikud unustada – peaasi, et nad alguses ja lõpus õigesti ritta saavad.

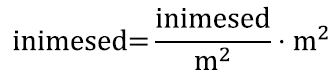
Sulle võivad huvi pakkuda need õppematerjalid:

Erinevat tüüpi võrrandid

Võrrandid võivad välja näha väga erinevad, näiteks kõik järgnevad on võrrandid:

Esimene erinevus on muidugi selles, et oleme muutujatele valinud erinevaid tähiseid. Mõned oleme tähistanud tähtedega, mõned sõnadega.

Erinevusi on aga teisigi: mõnes võrrandis on üks muutuja, mõnes mitu. Mõnes võrrandis on muutuja esimeses astmes, mõnes on ta kõrgemasse astmesse tõstetud. Mõnes võrrandis tolkneb ka mõni nullist erinev arv, mida nimetasime vabaliikmeks, teises on ainult muutujad.

Erinevat tüüpi võrrandid aitavad kirjeldada erinevaid tingimusi, kuid küsivad ka erinevate lahendusmeetodite järele.

Ühe muutujaga võrrand

Võrrandites VANUS – 4 = 12 ning x³ – 4x = 4 on mõlemas ainult üks muutuja ehk otsitav suurus. Kuna matemaatiliselt pole mingit vahet, kuidas muutujaid tähistada, eristab neid võrrandeid eelkõige aste, millel muutuja ette tuleb.

Esimest nimetataks lineaarvõrrandiks, kuna muutuja xkõige kõrgem aste on 1, teist kuupvõrrandiks, kuna muutuja kõige kõrgem aste on 3.

Kooliprogrammi kõige ohtlikum on muidugi ruutvõrrand, mille lahendivalemit nõutakse une- ja mängupealt. Seetõttu näitame ka, et see lahend ei ole sugugi müstilise päritoluga, vaid üsna selge matemaatilise arutluse tagajärg [lk 275].

Muidugi ei ütle keegi, et astmed peaksid ainult ühest suuremad olema. Nii räägitakse ka juurvõrranditest, kui mängu tuleb ka ruutjuur muutujast. Näiteks √x + 2 = 4.

Üldiselt on nii, et mida keerulisemad muutuja astmed on mängus, seda keerulisem on võrrandit ka lahendada.

Mitme muutujaga võrrand

Võrrandis võib muidugi ka olla mitu muutujat. Näiteks peatüki alguses toodud lauljate ja laululava pindalaga võrrand oli kahe muutujaga võrrand. Võrrand xⁿ + yⁿ= zⁿ on aga näiteks kolme muutujaga võrrand, kus non teadaolev arv.

Ühed lihtsamad mitme muutujaga võrrandid on kahe muutujaga lineaarvõrrandid, kus mõlemate muutujate aste peab olema üks. Näiteks x + 3y = 4 või 0,5x + y= 2 on kahe muutujaga lineaarvõrrandid.

Kuna siin on kaks muutujat, võime nende suhte kirja panna ka koordinaattasandil. Nendest võrranditest võib visuaalselt mõelda kui sirgetest: kõik arvupaarid, mis kahe muutujaga lineaarvõrrandit rahuldavad, moodustavad sirge tasandil.

Ka meie algne võrrand A = 3 · B on tegelikult sirge võrrand.

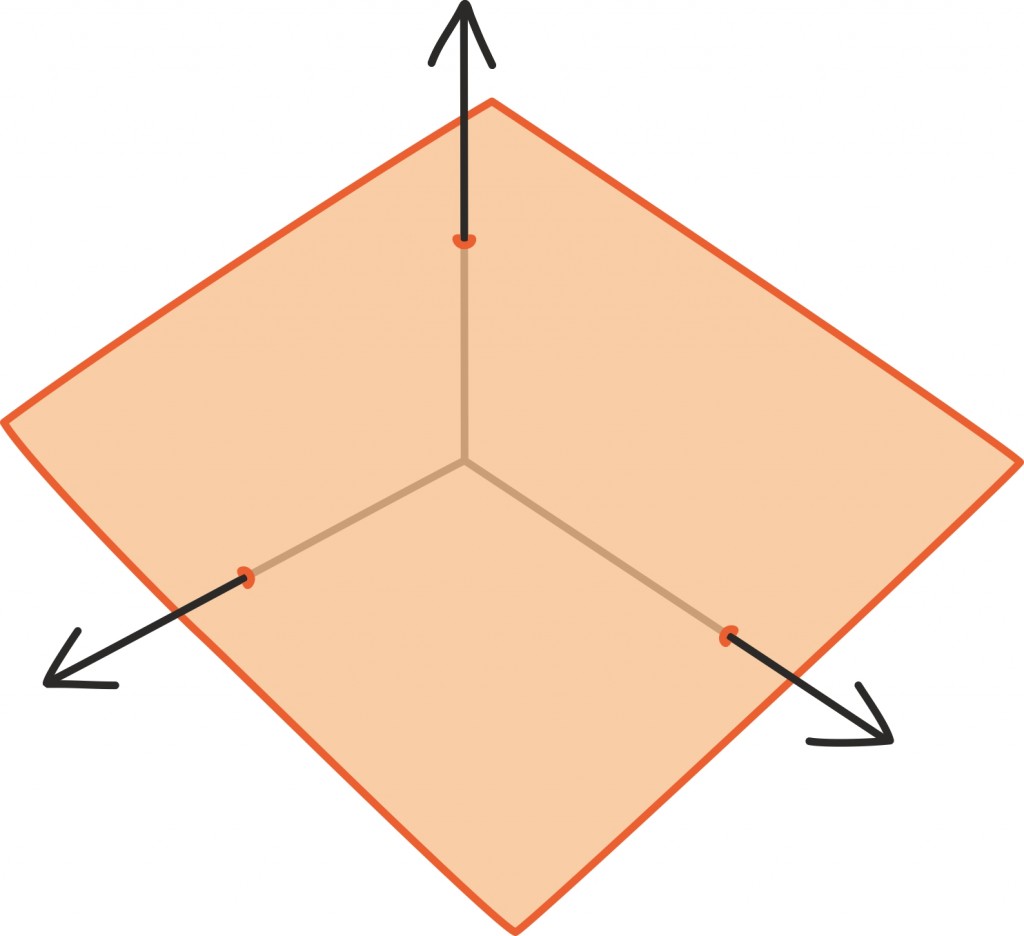
Sarnaselt moodustavad kõik arvukolmikud, mis rahuldavad kolme muutujaga lineaarvõrrandit, ühe ilusa tasandi.

Sirge ja tasandi võrrandist räägime muidugi varsti ka pikemalt [lk 184].

Keegi ei keela moodustada ka nelja, kuue või kahesaja liikmega võrrandeid. Näiteks on tore võrrand

Kas seda võrrandit oleks võimalik kuidagi ka tõlgendada? Üks pisut hullumeelne võimalus oleks öelda, et võrrandi lahendite hulk moodustab 27-mõõtmelises ruumis 26-mõõtmelise tasandi. Seda on aga pigem raske ette kujutada! Lihtsam on sellest võrrandist mõelda kui 27 sahkerdajast, kes jagavad omavahel ära kokku näpatud miljon eurot.

Võrrandisüsteem

Mõnikord ei õnnestu kõiki soovitavaid tingimusi ühe võrrandiga kirja panna. Otsitavad suurused rahuldavad mitut tingimust samaaegselt. Nii saamegi mitmest võrrandist koosneva võrrandisüsteemi. Võrrandisüsteemi lahendamine tähendab, et otsime suurusi, mis rahuldavad kõiki võrrandeid korraga.

Näiteks võib meil olla teada, et ristküliku kujuga toa pindala on kümme ruutmeetrikest ja ümbermõõt neliteist meetrit, ning meid huvitaks, mis kujuga see tuba on. Mis on toa pikkus ja mis tema laius?

Ümbermõõtu kirja pannes saame võrrandi:

Pindala kirjeldades aga võrrandi:

Et leida sobivat pikkust-laiust, peame nüüd üheaegselt lahendama mõlemad võrrandid.

Proovimise teel näeme, et näiteks PIKKUS = 1 ja LAIUS = 6 rahuldab esimest võrrandit, ent ei rahulda teist võrrandit. Samas PIKKUS = 10 ja LAIUS = 1 rahuldab esimest, kuid mitte teist võrrandit.

Üheaegselt lahendavad mõlemat võrrandit ainult:

PIKKUS = 2 ja LAIUS = 5
LAIUS = 2 ja PIKKUS = 5

Muidugi ei olnud võrrandil endal aimugi, kumba meie nimetasime toa „pikkuseks” ja kumba tema „laiuseks“, ning nii saamegi sisuliselt sama toa kuju kaks korda.

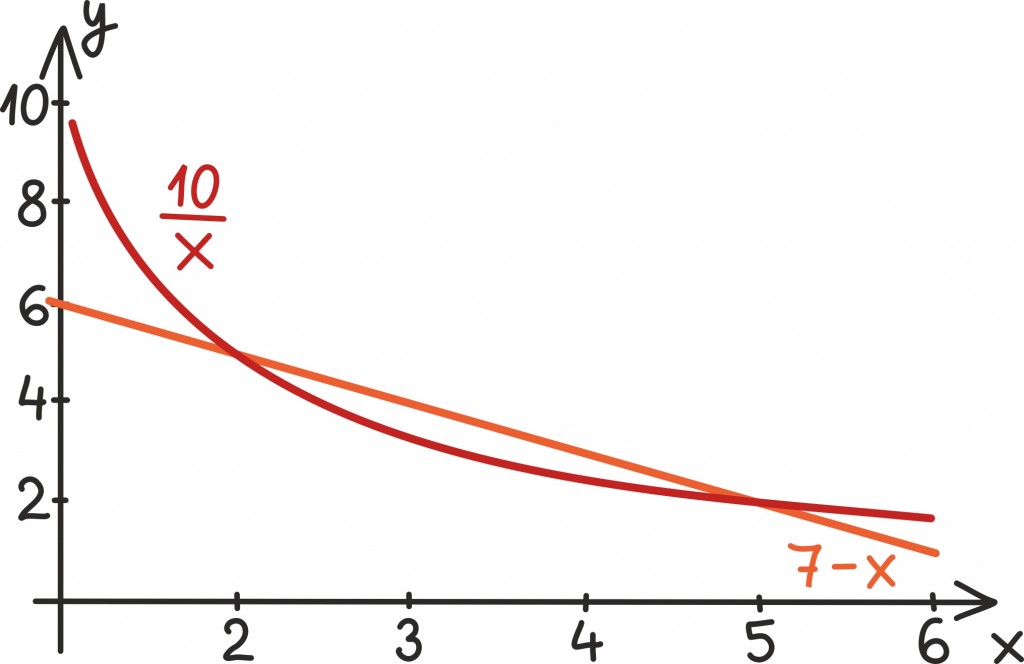
Kuna meil on kaks erinevat muutujat, võime jällegi seda võrrandisüsteemi ka geomeetriliselt ette kujutada. Nagu ennist, võime esimest võrrandit kirjeldada sirgega

teist võrrandit kirjeldab aga joon kujus

Nende kahe joone lõikepunktid annavadki meile lahendid:

Sellest räägime aga pikemalt juba võrrandite ja geomeetria peatükis [lk 184].

Mobiilioperaatori valimine

Võrrand ei ole mitte ainult üks tähtsamaid matemaatilisi seoseid, vaid on lisaks üks tihedamaid seoseid matemaatika ja meid ümbritseva vahel.

Nagu mainisime, aitavad võrrandid tingimusi ja olukordi täpselt ning matemaatiliselt kirja panna. Kui võrrandite lahendamisega tulevad suurepäraselt toime ka arvutid, siis nende kirjapanemine jääb siiski veel inimeste hooleks.

Võrrandite koostamiseks on väga hästi vaja lahti mõtestada olukord ning otsustada, millisel täpsusel seda kirjeldada. Milliseid nähtuseid, omadusi ja komponente peaksime arvesse võtma? Kuidas nad täpselt omavahel seotud on? Võrrandi kirjapanek on tähtis ja huvitav etapp, kus ebatäpsest elulisest probleemist saab täpne matemaatiline ülesanne.

Seetõttu kutsume lugejat veel kord kogu seda protsessi läbi tegema.

Oletame, et valid endale uut mobiilioperaatorit, kelle paketid on järgnevad.

Operaator A: 5 eurot kuumaks pluss 0,01 eurot kõneminut.
Operaator B: 1 euro kuumaks pluss 0,02 eurot kõneminut.

On üsna intuitiivne, et kui satume hoogu ja räägime ülemäära palju, siis peaks operaator A hinnapakett odavam tulema, sest kõneminuti hind on poole väiksem. Samas kui räägime väga vähe, on jällegi operaatori B pakett kasulikum.

Seega on üsna mõistlik ja oluline küsida: vähemalt kui mitu minutit peaks kuu jooksul rääkima, et tasuks valida operaator A?

Sellele küsimusele vastamiseks on üks võimalus koostada võrrand ja leida, millise kõneaja korral on operaatorite tasud võrdsed. Intuitiivselt on siis selge, et rohkem rääkides oleks kasulik valida operaator A ja vähem rääkides operaator B. Selle „rohkem kui” idee saaksime veel täpsemalt kirja panna võrratuste abil [lk 190].

Võrrandi koostamine

Rolli mängivad siin olukorras räägitud kõneminutite arv, kõneminuti hind ja kuumaks. Viimased kaks neist on lihtsalt arvud, kõneminutite arvu me alles otsime – tema on muutujaks ning võime tema väärust tähistada k-ga.

Kogutasu saamiseks peame kuutasule liitma kõneminutite ja minutihinna korru- tise. Kokku maksaksime siis kuus:

operaator A juures: 5 + 0,01k eurot,
operaator B juures: 1 + 0,02k eurot.

Tingimuse, et mõlema operaatori juures oleks kogumakse võrdne, võime siis kirja panna järgmiselt:

Võrrandi lahendamine

Nüüd võime kogu konteksti ära unustada ja võrrandi

muutuja k suhtes juba tunnis õpitud teisenduste varal ära lahendada:

Tegelikult oleme siin juba tunginud järgneva peatüki, võrrandite teisendamise ja lahendamise territooriumile, millest räägime kohe palju pikemalt ja põhjalikumalt.

Enne jääb vaid üle veel saadud lahendust tõlgendada.

Võrrandi tõlgendamine

Tuleb välja, et kuutasud on võrdsed, kui räägiksime täpselt 400 minutit. See teeb üle 10 minuti päevas, mis tundub ikka päris palju. Seega tasub ilmselt ikka valida operaator B.

Maatriks*