Uurime, millest sõltub ideaalgaasi poolt tehtava töö suurus.

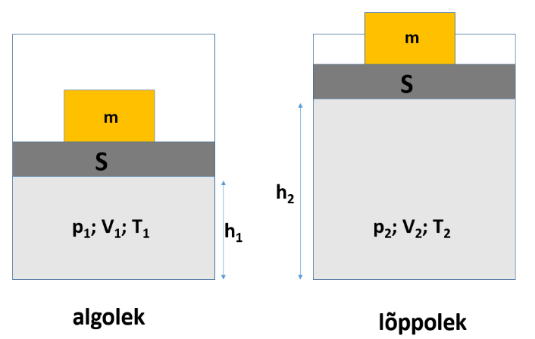
Asugu ideaalne gaas kolviga, mille põhjapindala on S suletud silindris. Asetame kolvile koormise, mille mass on m.

Arvutame kui suur töö tehakse selle koormise liigutamisel kui gaasi ruumala suureneb (gaas paisub) ning sellega kaasnev kolvi liikumine paneb liikuma sellel asuva koormise.

Gaasi olekuparameetrid (rõhk, ruumala, temperatuur) protsessi alguses on vastavalt T1, p1 ja V1 ning protsessi lõppedes T2, p2, V2.

Vaatleme lihtsuse mõttes olukorda, kus gaasi rõhk paisumise käigus ei muutu (isobaariline protsess – p1 = p2 = p).

Et kolb liigutab koormist teepikkuse s = h2 – h1 võrra ning kolbi liigutav jõud peab olema võrdne kolvile mõjuva rõhumisjõuga (p=F/S => F = pS), saame leida koormise liigutamiseks välisjõudude (kolbi liigutava gaasi) poolt tehtud töö:

A’= Fs = pS(h2-h1)= p(Sh2-Sh1)= pV2 – pV1

ehk

kus A’ – koormise liigutamiseks gaasi poolt paisumisel tehtud töö; p – gaasi rõhk isobaarilises protsessis ning ΔV – gaasi ruumala muutus.

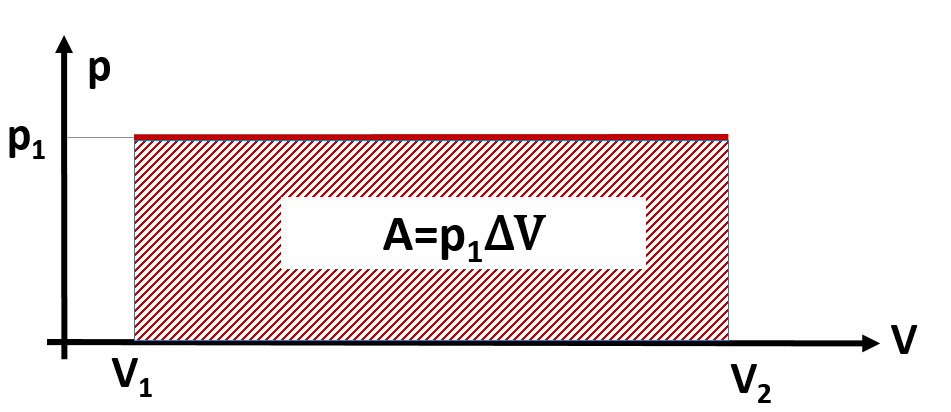
Kirjeldame gaasi paisumist Vp-teljestikus, näeme, et isobaarilise protsessi korral, on gaasi poolt tehtud töö võrdne Vp-teljestikku joonestatud paisumisprotsessi kirjeldava graafiku alla jääva kujundi pindalaga.

Taolist, graafiku alla jääva kujundi pindala leidmise teel suurusele väärtuse arvutamist nimetatakse graafiliseks integreerimiseks ning seda saab kasutada ka gaasi töö arvutamiseks kui gaasi rõhk protsessi käigus muutub.

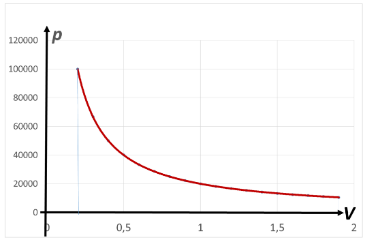
Isotermilise protsessi korral on graafikuks hüperbool ning selle alla alg- ja lõpp-ruumala tähistavate abijoonte vahele jääva kujundi pindala ongi võrdne isotermilises protsessis gaasi paisumisel tehtud tööga.